 |
Построение исходной системы (сети) доставки груза по сухопутному участку
|
|
|
|
Результаты расчетов, полученные в разделе 1, а именно поставщики и потребители (порты отправления) в сетевой транспортной задаче рассматриваются как источник и сток, соответственно. Необходимо построить исходную транспортную сеть с 6-8 промежуточными узлами с указанием расстояний в прямом направлении. Узлы транспортной сети должны иметь многочисленные связи, т.е. из одного пункта в другой должна наблюдаться вариация маршрутов доставки.
Например, если поставщик находится в Одессе, а потребитель в Курске, исходная сеть имеет следующий вид (рис. 2.1).
Рисунок 2.1 – Исходная сеть при построении рационального маршрута движения автотранспортных средств
Источник – Одесса, сток – Курск.
Количество сетей, которые необходимо построить определено решением задачи в первой главе. Полученное решение задачи, т.е. 
(объем материального потока от i -го потребителя до j -порта отправления) принимается как годовой грузопоток 
по маршрутам.
2.3. Нахождение оптимального маршрута
Задача отыскания оптимального маршрута от поставщиков к потребителям решается в соответствии с алгоритмом, представленным на рис. 2.2.
Приведем пример расчета для сети рис.2.1.
Задача состоит в отыскании кратчайшего расстояния в транспортной сети из Одессы в Курск. Рассматриваемая транспортная сеть является ацикличной, т.е. не содержит циклов и для отыскания кратчайшего расстояния между заданными пунктами может быть применен следующий алгоритм.
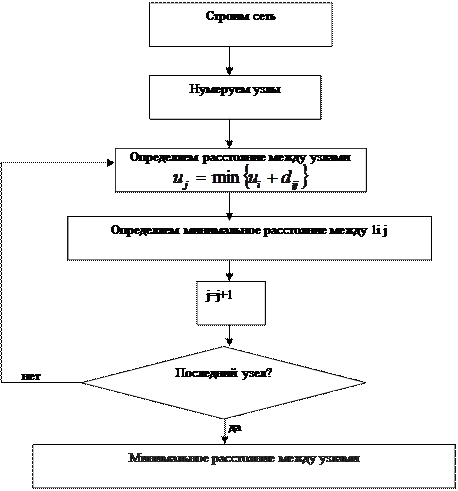
Рисунок 2.2 – Алгоритм нахождения минимального расстояния
Рассмотрим данный алгоритм на примере сети (рис. 2.1)
Пронумеруем узлы сети от 1 к p, таким образом, что если сеть содержит дугу (i,j), то i>j. Чтобы добиться выполнения этого условия, присвоим источнику или начальному узлу узлу номер 1. Зачеркнем это узел и все исходящие из него дуги и не будем их рассматривать в дальнейшем при присвоении номеров. Возьмем любой другой узел, имеющий только исходящие дуги и припишем ему номер 2. Зачеркнем этот узел и все исходящие из него дуги искрим из рассмотрения при дальнейшем рассмотрении номеров.
|
|
|
Определим расстояние между пунктами, имеющими соединительные дуги. Воспользуемся для этого картой Украины, России, Казахстана или Белоруссии (в зависимости от исходных данных и результатов рещшения задачи выбора поставщика) и сайтом www.lardi-trans.ru.
Представим найденные расстояния в табличной форме (табл.2.2)
Таблица 2.2 – Расстояния между пунктами перевозки, км
Далее, в соответствии с формулой (2.1) определяем потенциалы и находим для каждого узла сеты.
(2.1)
|
|
|
где 
- расстояния между связными узлами i и j;
- кратчайшее растояние между узлами 1 и j.
Определим потанциал u1 = 0
км (из узла 1);
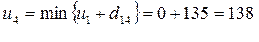км (из узла 1);
км (из узла 1);
км (из узла 1);
км (из узла 1);
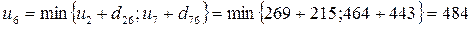(из узла 2);
(из узла 2);
(из узла 6);
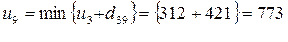
(из узла 3);
(из узла 4)
(из узла 5);
(из узла 5);
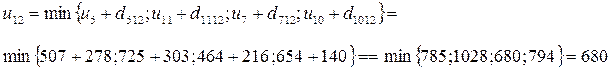(из узла 7);
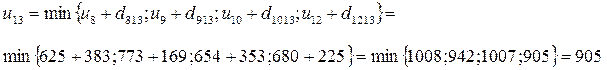(из узла 12).
Применяемый алгоритм нахождения маршрута следования в сетевом варианте позволил определить:
- минимальное расстояние между Курском и Одессой;
- построить оптимальный маршрут следования.
Итак, расстояние минимальное в Курск из Одессы составляет 905 км.
Выводы и результаты решения задачи поиска оптимального маршрута
В данном подразделе необходимо привести основные результаты по 2 разделу, а именно:
- указать тип выбранного автотранспорта;
- указать необходимое количество транспортных средств по каждому маршруту;
- привести исходную транспортную сеть с указанием на ней кратчайшего маршрута;
- указать кратчайшие расстояния по маршрутам.
Раздел 3. Построение системы управления запасами
|
|
|
