А. Статистические оценки и законы распределения.

 

Наиболее важными оценками статистических параметров (статистик) исходной информации, то есть значений того или иного геофизического поля x_i, являются оценки математического ожидания М _х, дисперсии Д _x, среднеквадратичного (стандартного) отклонения σ_х.

Оценка математического ожидания случайной величины x, распределенной по нормальному закону [2], есть ее среднее арифметическое значение

,

где n- объем выборки, x_i – i-е значение Х в данной выборке.

 

Дисперсия Д _х определяется как математическое ожидание квадрата отклонения случайной величины от ее среднего значения по формуле:

,

а стандартное отклонение σ_х:

σ_х=S_x= .

Кроме этих основных показателей необходимо зачастую оценивать и такие как размах выборки

Н=X_max-X_min,

асимметрия К=

и эксцесс

Самый удобный способ получить общее представление о структуре выборки – построение гистограммы. Она позволяет сгруппировать данные в пределах выбранного интервала значений и упорядочить такие группы (по возрастанию или убыванию значений). Интервал гистограммы, вообще говоря, можно выбирать произвольно, ориентируясь на ее форму и на предположения о наиболее вероятном типе теоретического распределения. Однако, в ряде приложений для примерной оценки длины интервала пользуются какой-либо эмпирической формулой, то есть формулой, построенной на основе опыта статистической обработки больших объемов информации. В данном пособии рекомендуется так называемая формула Стерджесса

Тогда число интервалов гистограммы j определяется просто как целая часть отношения Н/Δх.

Таким образом, гистограмма есть графическое изображение группировки выборки данных объема n по j интервалам Δх.

Если долю случайных наблюдений внутри интервала обозначить m_j, то гистограмма может быть представлена как распределение частот (рис.3.3). При этом площадь, ограниченная гистограммой и осью абсцисс оказывается равной единице, а сама гистограмма становится аналогом кривой плотности распределения случайной величины [2].

Зная выборочные оценки исследуемой совокупности можно пытаться аппроксимировать гистограмму той или иной кривой теоретического распределения. Гипотеза о виде распределения всегда выдвигается исследователем. При этом все определяется конкретной задачей, стоящей перед ним. Можно указать несколько типичных ситуаций [9].

1. Геофизик-исследователь сопоставлением выборочного и теоретического распределения проверяет справедливость построенной им вероятностно-статистической модели взаимодействия физического поля со средой или такой же модели геолого-геофизической обстановки. Здесь предполагается точное знание модельного теоретического распределения.

2. Геофизик-интерпретатор решает вопрос о принадлежности нескольких выборок данных к единой генеральной совокупности. Такие задачи нередко возникают при обработке больших объемов геолого-геофизических показателей с целью районирования территорий или с целью создания представительной модели среды.

3. Геофизик-интерпретатор нуждается в выборке с заданным типом распределения. Чаще всего это случается, когда математический аппарат, используемый интерпретатором, предполагает подобного вида ограничения на статистические свойства исходного материала. Например, методы регрессионного анализа в своей статистической постановке требуют нормального распределения отклонений наблюденных значений от линии регрессии [10].

Проверка гипотезы о виде распределения обычно выполняется с помощью критерия Пирсона (χ² – критерия) [10]. Его значение вычисляется следующим образом. Для центра каждого κ-го интервала гистограммы (их число не должно быть меньше пяти-семи) по выбранному типу распределения рассчитывается теоретическая частота Р_κ, а затем и теоретическое (ожидаемое) число наблюдений n Р_κ, попадающих в его пределы (это число не должно быть меньше 5-10, в противном случае интервалы следует укрупнить).

Если выборочные показатели в каждом интервале значительно отличаются от ожидаемых, то маловероятно, чтобы исследуемая выборка была извлечена из совокупности, отвечающей данному теоретическому распределению.

Вычисление критерия χ² производится по формуле

χ²=

где m_k – число наблюдений в k-ом интервале:

nPk – ожидаемое число наблюдений в том же интервале.

Полученное значение χ² сравнивается с теоретической величиной, которую следует отыскать в таблице χ² (ν,α) – распределения. Здесь ν – число степеней свободы (чаще всего это n-1); α – уровень значимости в процентах или относительных единицах. В геологии, как правило, ограничиваются 5%-ым уровнем [9].

 

 

Гипотеза о выбранном характере распределения принимается, если вычисленное значение χ² не превышает табличное.

Теория распределений применительно к вопросам разведочной геофизики развита еще недостаточно полно. Практически не вызывает сомнений лишь характер распределения погрешностей измерений в полевых геофизических экспериментах, который хорошо аппроксимируется нормальным (Гауссовым) законом

Этот закон вообще широко распространен в природе, ему подчиняется масса сложных вероятностных процессов, которые в свою очередь являются комбинацией большого числа разнородных случайных событий [9].

Однако, в геофизической практике может быть использовано и множество других закономерностей распределения случайных величин. В настоящем пособии кроме закона Гаусса при проверке гипотез о характере выборочного распределения есть возможность использовать логнормальное распределение

 

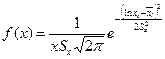
где - среднее значение и стандарт натуральных логарифмов x;

экспоненциальное распределение

равномерное распределение

где a<х<b;

 

 

гамма-распределение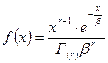

где , - гамма-функция аргумента ; распределение Пуассона

Р(х)= ,

где к= 0,1,2,3………

биномиальное распределение

где n – число интервалов, - номер текущего интервала.

Следует иметь ввиду, что в чисто геологических исследованиях, в отличие от прикладных геофизических, вопросам классификации распределений применительно к описанию геологических характеристик уделялось весьма большое внимание [10]. Поэтому имеется возможность, базируясь на тех или иных связях геологических показателей с геофизическими параметрами, использовать накопленные геологами статистические сведения для выдвижения обоснованных гипотез о типах распределений физических параметров геологических сред.

Для выполнения лабораторных работ по статистической модели интерпретации студенту придется воспользоваться электронным банком цифровой информации геопотенциальных полей и его матобеспечением.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: