 |
Парные корреляционные связи.
|
|
|
|
Методы прогноза, основанные на связи двух параметров – геологического (Н) и какого-либо геофизического (например Δg) – наиболее просты, однако, во многих случаях точность такого прогноза оказывается низкой (ошибка приближения ε – велика), поскольку из-за суммарного характера наблюденных геофизических полей не всегда удается подобрать геофизический параметр тесно корреляционно связанный с изучаемой геологической границей.
Наглядное представление о парной взаимосвязи анализируемых величин дают корреляционные графики (поля корреляции). На рис 3.6 приведен график корреляции глубин залегания кристаллического фундамента Нф и аномалий поля Δg, построенный по точкам эталонного пространства. Исходные профильные кривые Нф и Δg показаны на рис 3.7. Значения Нф и Δg в отсчетных точках профилей являются ординатами и абсциссами соответствующих точек на корреляционном графике. Вытянутость всего “облака” точек вдоль некоторой прямой характеризует тесноту линейной парной корреляционной связи Нф и Δg.Если поверхность Нф является достаточно сильной гравиактивной границей (скачок средневзвешенного значения плотности порядка 0.2г/см3 и более) и в толще осадочного чехла нет столь же резких перепадов плотности, экранирующих гравитационное влияние фундамента, то вязь Нф с Δg может быть действительно близка к линейной.
Тогда целесообразность ее аппроксимации прямой вида Нф=А0+А1Δg, называемой прямой парной регрессии, становится очевидной. Коэффициенты А0 и А1 в данном случае конкретизируют вид прогнозного оператора Аφ из уравнения (1).
Оптимальная аппроксимация, дающая наиболее вероятное положение линии регрессии на плоскости (Нф, Δg)φ, выполняется методом наименьших квадратов [10]. При этом минимизируется сумма квадратов отклонений ΔН исходных значений Нi от отсчетов, полученных по регрессионной прямой
|
|
|
(3.3)
Здесь N – объем выборки точек эталонного пространства φ. Дифференцируя (3) по неизвестным коэффициентам А0 и А1 с учетом линейности оператора суммирования 
, получим систему уравнений, которые принято называть нормальными [18]:
(3.4)
Решить систему (4) относительно А0 и А1 и таким образом конкретизировать вид оператора Аφ несложно. Действительно, из первого уравнения системы имеем
(3.5)
где 
и 
- средние значения Н и Δg эталонной выборки.
Умножим теперь первое уравнение на 
, второе – на N и рассмотрим их разность.
Отсюда получим
(3.6)
Более удобный вид для коэффициента А1 получается, если поделить числитель и знаменатель формулы (6) на N2:
(3.7)
Здесь 
- среднее значение произведения Н и Δg в пределах эталонной выборки;
- средний квадрат наблюденного поля Δg в пределах эталонной выборки.
В таком виде числитель и знаменатель в формуле (7) имеют смысл известных выборочных статистических оценок – ковариаций [18].
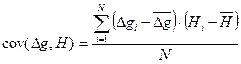(3.8)
и дисперсии
(3.9)
Убедиться в этом можно просто раскрыв скобки в формулах (8) и (9) с учетом того, что и в рамках используемой эталонной выборки – величины постоянные. Тогда коэффициент А1 запишется в компактном виде
(3.10)
Ковариация, как известно, является показателем тесноты взаимосвязи Δg и Н, однако, чтобы не учитывать размерности и размаха величин Δg и Н, удобнее пользоваться нормированной оценкой, называемой коэффициентом корреляции [18]:
(3.11)
где D(Н) – оценка дисперсии глубин Н на используемой эталонной выборке.
Пределы изменения этой величины определяются соотношением
-1≤r(Δg,Н)≤1 (3.12)
Равенство r=нулю означает полное отсутствие линейной связи между величинами Δg и Н (при этом другой, нелинейный, тип связи отнюдь не исключен). По мере приближения r к ±1 статистическая (корреляционная) связь параметров стремится к линейной функциональной зависимости.
|
|
|
Теперь с учетом (5) и (7) уравнение линейной регрессии Н=А0+А1∆g можно представить в следующем виде
(3.13)
Отсюда 
(3.14)
Используя статистические оценки (8) и (9), получим
(3.15)
или, имея в виду формулу (11):
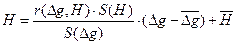(3.16)
Здесь 
, 
- оценки среднеквадратических отклонений (стандарты) величин ∆g и Н в пределах эталонной выборки [18].
Таким образом, из формулы (16) хорошо видно, что коэффициенты оператора связи Aφ в данном случае определяются теснотой корреляции геолого-геофизических параметров и величинами их стандартов.
Погрешность вычисления коэффициентов характеризуется среднеквадратической ошибкой подсчета корреляции:
(3.17)
Следовательно, увеличением мощности эталонной выборки достигается более точная аппроксимация зависимости Н от ∆g.
Однако, получив близкую к единице величину r(∆g,H) и малую ошибку δ(r), еще нельзя утверждать, что значения Н определяются найденным регрессионным оператором в точках эталонного пространства с требуемой для прогнозирования точностью.
Наилучшим показателем в этом смысле является вычисляемая в прогнозной постановке задачи (2) среднеквадратическая ошибка прогноза (приближения) Н по ∆g:
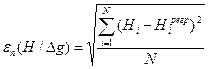(3.18)
где 
- значения Н из уравнений (13) - (16).
Если в формулу (18) подставить Н из уравнения (16) и провести соответствующие преобразования, нетрудно получить выражение для 
в несколько ином виде:
(3.19)
Здесь хорошо видно, что ошибка приближения тем больше, чем больше природная дисперсия Н и уменьшается с возрастанием тесноты корреляционной взаимосвязи Н и ∆g.
Положим, например, стандартное отклонение Нф равным 500м (такое значение S(Н) характерно для ряда площадей бортовой зоны Прикаспийской впадины), тогда при r(∆g,H)=0,9 ошибка приближения по формуле (19) составит 218м. Таким образом, высокое само по себе значение коэффициента корреляции в конкретных геолого-геофизических условиях оказалось недостаточным для прогноза с малой ошибкой.
Как уже говорилось, во многих случаях парная корреляционная взаимосвязь геолого-геофизических параметров оказывается довольно слабой. Это чаще всего объясняется суммарным характером большинства геофизических полей. Аномалии ∆g, например, обусловлены помимо одной-двух резких гравиактивных поверхностей, целым рядом слабых плотностных границ геологического разреза, конфигурация которых может существенно отличаться от формы поверхности сильных границ. Указанное обстоятельство ослабляет корреляцию ∆g с Н и, следовательно, способствует увеличению εn.
|
|
|
|
|
|
