 |
Построение модели объема выпуска продукции
|
|
|
|
Задание 4. ЗАДАЧА НЕЛИНЕЙНОЙ МНОГОФАКТОРНОЙ РЕГРЕССИИ
1. Построить экономическую модель выпуска продукции, которая характеризует связь между результативным признаком (y) и объясняющими факторами (х1,х2), применив линейную (y = a0 + a1x1 + a2x2 + u) и степенную 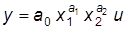 зависимости. Для построения и расчета модели использовать семь наблюдений.
зависимости. Для построения и расчета модели использовать семь наблюдений.
2. Оценить достоверность модели и статистическую значимость параметров.
3. Определить точечный и интервальный прогнозы выпуска продукции при заданных значениях факторов.
4. Выполнить экономико-математический анализ модели. Дать рекомендации по управлению объёмом выпускаемой продукции на основании анализа характеристик взаимосвязей объясняющих переменных модели.
5. Для выполнения задания применить пакет электронных таблиц «Excel», стандартные программы «ЛИНЕЙН», «Регрессия» и матричный подход, реализующий метод наименьших квадратов (МНК) для модели линейной регрессии.
6. Исходные данные для выполнения задания 1 приведены в табл. П.4.1.
Построение модели объема выпуска продукции
Для построения заданной модели y = f (x1,x2,u) (функции Кобба – Дугласа) необходимо идентифицировать переменные, входящие в модель. Здесь у – результативный признак (объем выпуска продукции); х1, х2 – объясняющие переменные, где х1 – производительность труда, х2 – затраты производственных фондов.
Спецификация модели производственной функции имеет вид
у = f (x1, x2, u),
где u – случайная величина, которая учитывает влияние неучтенных в модели факторов на объем выпуска продукции.
Аналитическую форму модели выпуска продукции представим в двух формах:
а) линейная: у = а0 + а1х1 + а2х2 + u;
б) степенная: 
Соответственно расчетные функции для выборочной совокупности будут следующие:
|
|
|
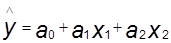 ; ;
| (4.1) |
 , ,
| (4.2) |
где аj – оценка j–го фактора модели (j = 1, 2).
Заметим, что полученная функция Кобба – Дугласа в модели объема выпуска продукции путем простейших преобразований может быть сведена к линейно-логарифмической функции. Для этого прологарифмируем левую и правую части модели, в результате получим уравнение вида
ln y = ln a0 + a1ln x 1 + a2 ln x 2.
Путем замены У = ln y; A0 = ln a0; X1 = ln x 1; X2 = ln x 2 степенная модель сводится к линейной, если входные данные для ее построения брать не в абсолютных единицах измерения, а в логарифмах.
Тогда получим уравнение вида:
Y = A0 + a1 X1 + a2X2 + u,
или в матричной форме
Y = XA + u,
где Y – вектор зависимой переменной (объем выпуска продукции, размерность (n  1),
1),
Y(n´1) =  ,
,
где n – количество наблюдений или объем выборки;
Х – матрица объясняющих переменных, размерность (n ´ (m + 1)),
X(n´(m+1)) =  ,
,
где m – количество факторов, входящих в модель;
А – вектор параметров модели, размерность ((m + 1) ´ 1),
A((m+1)´1) = 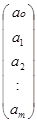 ;
;
u – вектор случайных величин или ошибок, размерности (n´1),
u(n  1) =
1) =  .
. 
На основании семи наблюдений (n = 7), применяя одношаговый метод наименьших квадратов(1МНК), определим неизвестные параметры линейной и степенной моделей. Система нормальных уравнений для задания 4 имеет вид
 а0n+a1
а0n+a1  +a2
+a2 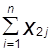 =
= 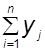 ;
;
а0  +a1
+a1  +a2
+a2  =
= 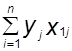 ; (4.3)
; (4.3)
а0 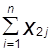 +a1
+a1  +a2
+a2  =
= 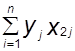 .
.
Система нормальных уравнений для степенной модели записывается следующим образом:
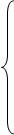 А0n+a1
А0n+a1 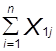 +a2
+a2 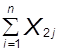 =
=  ;
;
А0  +a1
+a1 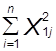 +a2
+a2  =
=  ; (4.4)
; (4.4)
А0 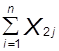 +a1
+a1 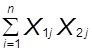 +a2
+a2  =
=  .
.
Решив системы уравнений (4.3) – (4.4), определим неизвестные параметры выборочной модели объема выпуска продукции.
Оператор для определения неизвестных параметров модели выпуска продукции в матричном виде имеет вид
А = (Х/Х)-1Х/У,
где Х – матрица объясняющих переменных;
Х/ – матрица, транспонированная к матрице Х;
У – вектор зависимых переменных;
А – вектор оценок параметров модели.
|
|
|
Примечание. Для проверки правильности полученных результатов применить стандартную программу «ЛИНЕЙН».
Для этого в разделе «Статистические функции» отметить курсором функцию «ЛИНЕЙН» и ввести необходимые аргументы:
– «Известные значения у» – множество значений у;
– «Известные значения х» – множество значений х, которое содержит одну (парная регрессия) или несколько переменных (многофакторная регрессия);
– «Конст» – логическое значение; если параметр «Конст» принимает значение «ложь», то предполагают, что свободный член в модели линейной регрессии а0 = 0, т.е. рассматривают модель без свободного члена вида у = а1х1 + а2х2 +…+аmxm; если параметр «Конст» принимает значение «истина», то при определении неизвестных параметров модели вычисляется параметр а0 (в данном случае рассматривается линейная модель со свободным членом)
У = а0 + а1х1 + а2х2 +…+ аmxm;
– «Статистика» – логическое значение, которое указывает, следует ли рассчитывать дополнительную статистику для регрессионной модели; если параметр «Статистика» имеет значение «истина», то стандартная функция «ЛИНЕЙН» вычисляет дополнительную регрессионную статистику виде массива (рис. 4.1).
| am | am-1 | … | a1 | a0 |
 am am
|  am-1 am-1
| … |  a1 a1
|  a0 a0
|
| R2 | sn | |||
| F | Степень свободы m - n | |||

| 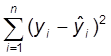
|
Рис. 4.1. Статистика функции «ЛИНЕЙН»
Здесь aj – оценка параметра aj, j = 1,`m;
a0 – оценка свободного члена регрессии;
 aj – стандартная ошибка оценки параметра модели;
aj – стандартная ошибка оценки параметра модели;
R2 – коэффициент детерминации;
 n – стандартная ошибка остатков (случайных величин);
n – стандартная ошибка остатков (случайных величин);
F – F–критерий;
Значение степени свободы равно (n – m), где n – количество наблюдений, m – количество переменных (факторов) в модели, включая точку пересечения. Количество степеней свободы необходимо для определения табличного значения F–критерия.
 – сумма квадратов, объясняющих регрессию (SSR);
– сумма квадратов, объясняющих регрессию (SSR);
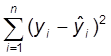 – сумма квадратов ошибок, которая объясняется наличием ошибки (U) в модели.
– сумма квадратов ошибок, которая объясняется наличием ошибки (U) в модели.
Если параметр «СТАТИСТИКА» имеет значение «ЛОЖЬ» или его пропустили, то стандартная функция «ЛИНЕЙН» вычисляет лишь неизвестные коэффициенты регрессии aj и константу a0.
|
|
|


