Главная | Обратная связь | Поможем написать вашу работу!

Задание 5. Задача линейной многофакторной регрессии

1. Построить эконометрическую модель, описывающую линейную зависимость результативного признака от факторов, входящих в модель. Применить 1МНК для оценки неизвестных параметров модели.

2. Определить дисперсионно-ковариационную матрицу параметров модели.

3. Проверить достоверность эконометрической модели и статическую значимость ее параметров.

4. Применить алгоритм пошаговой регрессии для построения эконометрической модели с наибольшим количеством значимых параметров.

5. Определить интервальные оценки для параметров эконометрической модели, полученной в п. 4.

6. Построить точечный и интервальный прогнозы для прогнозных и средних значений зависимых переменных по модели, полученной в п. 4.

В качестве исходных данных для выполнения задания 5 приведены показатели производственно-хозяйственной деятельности 50 машиностроительных предприятий. Варианты приведены в табл. П.5.1.

В табл. 5.1 приведены индексы результативного признака (Y), объясняющих переменных (X_i) и номера предприятий для каждого варианта. Например, для варианта № 90 в табл. П.5.1 приведены следующие данные: результативный признак Y₂ – индекс снижения себестоимости продукции; объясняющие переменные:

X₅ – удельный вес рабочих в составе ППП (производственно-промышленного персонала);

X₉ – удельный вес потерь от брака;

X₁₂ – среднегодовая стоимость основных производственных фондов;

X₁₆ – оборачиваемость ненормируемых оборотных средств;

X₁₇ – непроизводственные расходы;

предприятия машиностроения с номерами 11 – 50.

Исходные данные для результативного и факторного признаков для заданных предприятий приведены в табл. П.5.2. Тогда исходные данные для варианта № 90 имеют вид

Номер предприятия	Y₂	X₅	X₉	X₁₂	X₁₆	X₁₇
	-0,66	0,68	0,42	45,44	11,52	25,68
	1,41	0,74	0,05	41,08	17,28	18,13
¼
	2,84	0,80	0,13	25,76	14,04	11,64

В задании 5 рассматриваются следующие показатели:

У₁ – производство труда;

У₂ – индекс снижения себестоимости продукции;

У₃– рентабельность;

У₄ – трудоёмкость единицы продукции;

У₅ – удельный вес рабочих в составе ППП;

У₆ – удельный вес покупных изделий;

У₇– коэффициент сменности оборудования;

У₈ – премии и вознаграждения на одного работника;

У₉ – удельный вес потерь от брака;

У₁₀ – фондоотдача;

У₁₁ – среденегодовая численность ППП;

У₁₂ – среднегодовая стоимость ОПФ;

У₁₃ – среднегодовой фонд заработной платы ППП;

У₁₄ – фондовооружённость труда;

У₁₅ – оборачиваемость нормируемых оборотных средств;

У₁₆ – оборачиваемость ненормируемых оборотных средств;

У₁₇ – непроизводственные расходы.

1. Эконометрическая модель, описывающая нелинейную зависимость результативного признака от факторов модели, имеет вид

где е – случайная величина, которая объединяет влияние неучтённых в модели факторов. В матричной форме уравнение линейной регрессии имеет вид

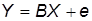где У – вектор-столбец размерности (n x 1) наблюдений за зависимой переменной У;

Х – матрица размерности n x (p + 1) n наблюдений за p переменными x_i;

В – вектор размерности ((р + 1) x 1) неизвестных параметров;

е – вектор разности (n x 1) n случайных величин e_i.

Вектор неизвестных параметров определяется по формуле

где X^/ – матрица, транспонированная к матрице X;

(X^/X)^-1– обратная матрица произведения матриц объясняющих переменных и транспонированной матрицы X^/.

Для проверки полученных результатов применить стандартную программу «ЛИНЕЙН».

2. Построение дисперсионно-ковариационной матрицы параметров модели.

Прежде чем перейти к построению дисперсионно-ковариационной матрицы параметров эконометрической модели, следует определить несмещённую оценку дисперсии случайных величин.

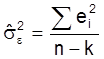где е_i – случайная величина (ошибка), i = 1,`n;

n – количество наблюдений;

k – количество параметров модели, включая пересечение.

В матричной форме величина определяется по формуле

где e^/ – вектор, транспонированный к вектору случайных величин, т.е. строка.

Теперь можно переходить к построению дисперсионно-ковариационной матрицы параметров регрессии, которая позволяет определить ковариацию (связь) между двумя парными их значениями, т.е. между b_i и b_j; i ¹ j. Тогда дисперсионно-ковариационная матрица параметров примет вид

В матричной форме

где – оценка дисперсии случайной величины;

(х’x)^-1 – обратная матрица к матрице (х’х).

Тогда оценки дисперсии параметров , , …, 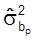определяют как элементы главной диагонали дисперсионно-ковариационной матрицы.

3. Проверка достоверности модели и статистической значимости его параметров.

Прежде всего определим множественный коэффициент детерминации и корреляции модели, которые характеризируют качество модели.

Множественный коэффициент детерминации определяется следующим образом:

Учитывая известное соотношение между коэффициентами детерминации и корреляции 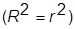, можно вычислить коэффициент корреляции

Теперь проверим достоверность эконометрической модели по критерию Фишера:

где k – количество параметров регрессионной модели, включая пересечение;

n – количество наблюдений.

Уровень значимости α, который лежит в пределах 0,5% ≤ α ≤ 10%, студент задает самостоятельно.

Если построенная модель соответствует реальной действительности, то переходим к определению статистической значимости ее параметров. Для этого воспользуемся t-статистикой.

Проверим значимость коэффициента корреляции с помощью t–критерия Стьюдента:

Определяем критическое значение по таблицам Стьюдента или воспользуемся стандартной функцией «СТЬЮДРАСПОБР» в разделе «Статистические» при заданном уровне значимости α и количестве степеней свободы (n – k). Если t > t_α/2, то с вероятностью не менее (1-α)·100% можем утверждать, что коэффициент корреляции статистично значим. Затем проверяем статистическую значимость каждого параметра модели b₀, b₁, b₂, …, b_p. Для этого определяем t-статистику для каждого параметра:

с (n - k) степенями свободы, где β_i^* – оценка параметра β_i, полученная методом наименьших квадратов;

β_i- гипотетическое значение, которое может принимать параметр β_i;

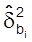– оценка дисперсии параметров;

n – количество наблюдений;

k – общее количество оцениваемых параметров.

Для базовой гипотезы статистики H₀: β_i= 0

t-статистика для параметров имеет вид

Полученное значение t-статистики для каждого параметра модели сравниваем между собой и определяем самый статистично незначимый параметр b_j, который соответствует фактору x_j.

4. Исключаем самый статистично незначимый фактор x_j и рассчитываем четырёхфакторную модель, т.е. повторяем шаги с 1-го по 3-й.

Эти шаги повторяем до тех пор, пока не убедимся, что все коэффициенты полученной модели статистично значимы. В этом случае мы определим факторы, которые оказывают наибольшее влияние на результативный признак. Другими словами, мы определим факторы, которые оказывают существенное влияние на функциональную связь модели.

5. Убедившись в достоверности модели и статистической значимости её параметров, определим интервальные оценки для каждого параметра:

6. Прогнозирование экономических показателей машиностроительных предприятий по модели многофакторной регрессии.

Точечный прогноз определяется по формуле:

или в матричной форме

где

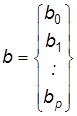Построение интервалов доверия для прогнозного значения математического ожидания результативного признака производим по формуле

Определение интервального прогноза для результативного признака производим по формуле

где – вектор прогнозных значений,

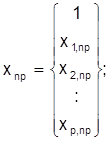
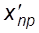– транспонированный вектор прогнозируемых значений объясняющих переменных.

⇐ Предыдущая 1 23

Воспользуйтесь поиском по сайту: