 |
Дифференцирующее устройство
|
|
|
|
Поменяв местами R и С в функциональной схеме интегрирующего устройства, получим функциональную схему дифференцирующего усилителя, рис.20.8.
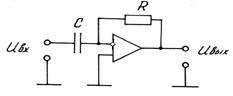
Рис. 20.8. Функциональная схема дифференцирующего устройства
В этом случае применение закона Кирхгофа для
узла 1 дает следующее соотношение:
С(dUвх/dt)+Uвых/R=0, (20.7)
Откуда Uвых=-RCdUвх/dt
АЧХ дифференцируещего устройства можно выразить
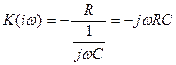; K(ω)=ωRC. (20.8)
Как видно из этого выражения, с увеличением частоты K(ω) возрастает. Идеальный дифференцирующий усилитель должен иметь K(f)®¥ при f ®¥. Однако практически невозможно это реализовать. Начало частотной характеристики определяется равенством 1/ωC=R, в этом случае К (f) = 1.
В рабочей области частот K(f) должен возрастать + 6 дБ на октаву или + 20 дБ на декаду. После точки А К(f) дифиринцирующего устройства и К¢(f) ОУ совпадают.
Логарифмирующее устройство
Логарифмирующее устройство предназначено для получения выходного напряжения, пропорционального логарифму входного сигнала. Функциональная схема логарифмирующего устройства приведена на рис.20.9.
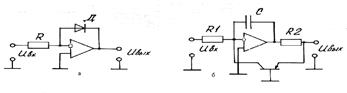
Рис. 20.9. Функциональная схема логарифмирующего усилителя
а – с диодом; б – с транзистором
В логарифмирующем устройстве используется диод, характеристика которого описывается выражением:
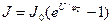, (20.9)
где I0 - обратный ток утечки р-n перехода;
jТ - термический потенциал, jТ =KT/q;
при Т =20°С, jТ =26 мВ;
U- напряжение, приложенное к диоду.
При U > 26 мВ вольт-амперную характеристику диода можно представить Iд=I0eU/jT . Прологарифмировав обе части, запишем:
ln Iд =lnI0+U/jТ или U=jT(ln Iд -lnI0) = jТlnIд/I0
Напряжение, приложенное к диоду, U=Uвых.
Uвх/R+Iд=0, Iд=- Uвх/R.
Поэтому Uвых=-jТlnUвх/I0R, это выражение в десятичных логарифмах имеет вид;
|
|
|
Uвых =-2,3jТlg Uвх/I0R
Диоды обладают паразитным омическим сопротивлением, на котором при больших токах падает существенное напряжение, приводящее к искажению логарифмической характеристики. Поэтому удовлетворительная точность в схеме с использованием диодов может быть получена при изменении Ubx в пределах 2 декад. Применение транзистора вместо диода (рис.20.9,б) позволяет значительно расширить динамический диапазон логарифмического устройства. В этой схеме небольшое сопротивление R2 включено в цепь эмиттера для уменьшения усиления транзистора, а конденсатор С обеспечивает устойчивость работы.
Тем не менее, параметры, как диода, так и транзистора сильно подвержены влиянию температуры. Поэтому в логарифмических усилителях стараются скомпенсировать влияние обратного тока.
Лекция №21
Активные фильтры
Общие сведения об активных фильтрах
Как известно, для получения избирательных характеристик в обычной схемотехнике широко используются LС - фильтры. Однако в интегральной схемотехнике индуктивности трудно реализуемы.
Поэтому в интегральной схемотехнике широкое применение находят активные фильтры, представляющие собой пассивные RС - фильтры, включенные в цепи инвертирующих и неинвертирующих усилителей. Другими словами, активные фильтры - это усилители на основе ОУ в сочетании с пассивными RС - фильтрами. Активные фильтры (АФ) находят самое широкое применение в качестве УВЧ, УПЧ, регуляторов тембров и т.д. Избирательная АЧХ АФ реализуется благодаря применению RС - пассивных фильтров. Следовательно, для анализа АФ необходимо знать характеристики пассивных фильров.
Пассивные RС – фильтры
Различают фильтры нижних частот (ФНЧ), полоса пропускания которых распологается в области нижних частот; фильтры высоких частот (ФВЧ), пропускающие сигналы высоких частот; полосовые и заграждающие (режекторные фильтры). Рассмотрим схему ФНЧ, рис.21.1a.
|
|
|
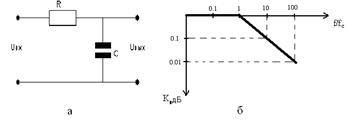
Рис.21.1. ФНЧ и его передаточная характеристика
Комплексный коэффициент передачи этого RC-фильтра определяется:
K(jω)=Uвых/Uвх=1/(1+jωRC).
Передаточная характеристика ФНЧ имеет выражение:
;
где fc -частота среза, равная 1/2pRC.
В соответствии с выражением (21.1) построим передаточную характеристику ФНЧ, рис.21.1,б.
При частотах f<<fc f/fc<< 1; K(f)=1 KдБ =0,
При частотах f>>fc f/fc >>1; K (f)=fc/f.
Полоса пропускания фильтра определяется частотой среза. При дальнейшем увеличение частоты имеет место затухание сигнала, т.е. спад частотной характеристики 20 дБ/дек. Если ФНЧ имеет несколько звеньев, то спад АЧХ равен n 20 дБ/дек.
Рассмотрим принципиальную схему ФВЧ, рис. 21.2.
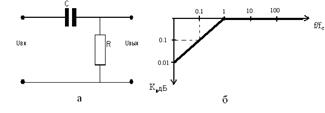
Рис.21.2. ФВЧ и его передаточная характеристика
Передаточная характеристика ФВЧ определяется выражением
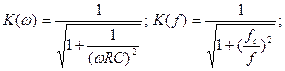
В области низких частот, где при f<<fс fс/f<<1 K(ω)=ωRC; K (f)=f/fc;
при f>>fc fc/f>>1 K(ω)=1; KдБ=0 дБ.
Для построения полосовых и заграждающих АФ широкое применение находит 2Т фильтр, рис. 21.3.
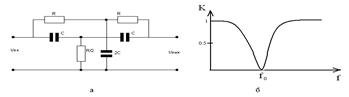
Рис.21.3. 2Т-фильтр и его передаточная характеристика
2Т филтр пропускает все частоты с коэффициентом передачи К=1, кроме квазирезонансной. На квазирезонансной частоте f0=1/2pRC коэффициент передачи равен нулю.
|
|
|
