Шесть функций сложного процента.

Сложные проценты применяют в тех случаях, когда процент по кредитам (ссудам) выплачивают не сразу, а его присоединя­ют к сумме долга с последующим определением наращенной суммы FV. Такая процедура начисления «процент на процент» называется капитализацией. Наращение идет по сложному про­центу в геометрической прогрессии, а процесс компаудинга (на­копления) описывается уравнением FV= PV(1+i)ⁿ

В свя­зи с этим для расчета процентной суммы используется следую­щая формула:

где i — годовая ставка;

n — количество периодов начисления;

m — число периодов начисления;

n*m — общее число периода начисления.

Когда интервалы между очередными платежами постоянны, то такую последовательность называют финансовой рентой или аннуитетом. Аннуитет (серия равновеликих платежей в течение n-периодов) называется обычным, если платежи осуществляются в конце каждого периода, и авансовым, если платежи осуществ­ляются в начале каждого периода.

Первая функция сложного процента — аккумулированная сум­ма капитала. Мы уже убедились, что в отличие от простого про­цента сложный предполагает, что доход приносит не только пер­воначальная сумма, но и полученный ранее процент на нее. Для определения стоимости, которую будет иметь капитал через не­сколько лет FV при использовании процедуры сложных процен­тов, используют формулу, отражающую процесс аккумулирования (компаундинга), наращения в соответствии с геометрической про­грессией: FV= PV(1+i)ⁿ

где FV— аккумулированная (будущая) сумма капитала;

PV — текущая стоимость (стоимость инвестиций в начальный пери­од);

i — ставка процента (например, i = 0,10, т.е. 10%);

n — количество периодов начисления.

Эта формула в финансово-экономических расчетах и опреде­ляет первую функцию сложного процента, а выражение (1+i)ⁿ называется множителем (коэффициентом) наращения или буду­щей стоимостью единицы аккумулированного капитала F₁: F₁= (1+i)ⁿ

где F₁ рассчитывается или определяется по таблице сложных процентов.

Таким образом, процесс аккумулирования депонированно­го, или инвестированного, капитала есть процесс накопления денег по заданной ставке i в течение определенного периода времени п.

При более частом, чем один раз в год, аккумулировании фак­тически полученный доход в конце года включает начисленные в году проценты. В связи с этим различают годовую номиналь­ную и годовую фактическую (эффективную) процентные ставки.

Годовая фактическая ставка — это годовая ставка, учитыва­ющая начисленные сложные проценты. Расчет годовой факти­ческой ставки ведется как процентное отношение дохода к ка­питалу в конце года, к величине капитала в начале года; в прак­тике фактическую ставку называют эффективной.

Вторая функция сложного процента — это будущая стоимость п-периодного аннуитета. Рассмотрим серию равновеликих и рав­номерных платежей (вкладов) под процент на определенное ко­личество периодов, при том что в каждом периоде производятся вклады капиталов (РМТ) одной и той же величины (серия вкла­дов — аннуитет). Этот поток платежей и есть аннуитет.

Наращенная сумма ренты (n-периодного аннуитета) пред­ставляет собой сумму всех членов ренты с начисленными на них процентами к концу ее срока.

Аннуитет называется обычным, если платежи осуществляются в конце каждого периода (рента пост- нумерандо), и авансовым, если платежи осуществляются в нача­ле каждого периода (рента пренумерандо).

Наращенная сумма рен­ты n-периодного аннуитета будет равна:

где (1 + i)ⁿ – 1/f = F₂ — вторая функция сложного процента.

В финансовых расчетах последнее выражение также называ­ют фактором фонда накопления или будущей стоимостью п- периодного аннуитета с платежом в одну денежную единицу (см. таблицу сложных процентов Инвуда).

В отличие от обычного аннуитета при авансовом аннуитете (пренумерандо) первый платеж осуществляется в начале перво­го периода, т. е. он приносит доход в течение всех n-периодов. Каждый последующий платеж работает на один период меньше, чем предыдущий, наконец, последний платеж приносит доход в течение только одного периода. Как и в случае обычного анну­итета, будущие стоимости каждого платежа образуют геометри­ческую прогрессию со знаменателем (1 + i), а первый член этой прогрессии — РМT(1 + i). Используя формулу расчета суммы и членов геометрической прогрессии, получим:

В этом случае фактор фонда накопления F₂ (будущая сто­имость авансового аннуитета с платежом в одну денежную еди­ницу) будет равен:

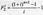
Третья функция сложного процента (обратная второй) — фак­тор фонда возмещения капитала. Из второй функции имеем:

Где i/ (1+i)ⁿ–1 = F₃ — фактор фонда возмещения, третья функция сложного

процента.

Коэффициент F₃ показывает денежную сумму, которую не­обходимо вносить в конце каждого периода для того, чтобы че­рез определенное число периодов остаток на счете составил одну денежную единицу; причем данный фактор учитывает получае­мый по взносам процент.

Можно сравнить фактор фонда накопления F₂ и фактор фонда возмещения F₃ Видно, что функция F₃ при фиксированных n и i есть величина, обратная фактору фонда накопления F₂ т.е.

Сравнивая фактор фонда накопления (будущую стоимость авансового аннуитета с платежом в одну единицу) и фактор аван­сового фонда возмещения, получим соотношение:

Четвертая функция сложного процента (обратная первой) — это текущая стоимость будущего денежного потока, т.е. текущая стоимость денег (инвестиций), PV определится из выражения:

Где 1/ (1+i)ⁿ = F₄ — четвертая функция сложного процента, текущая стоимость будущей единицы.

Сравнивая полученную формулу с фактором первой функции, видим:

Процесс пересчета будущей стоимости денежной суммы (по­тока денег); FV в настоящую называется дисконтированием, а ставка, по которой осуществляется дисконтирование, часто на­зывают ставкой дисконта.

C по­мощью функции F. можно ответить на два вопроса:

1. Сколько будет стоить сегодня сумма, которую получит ин­вестор через л-периодов?

2. За сколько нужно купить объект (сколько нужно вложить в объект), чтобы в результате будущей его продажи через n-пе­риодов обеспечить требуемую норму дохода на?

Пятая функция сложного процента — это текущая стоимость аннуитета. Как и предыдущая, данная функция связана с про­цессом дисконтирования. Пятая функция определяет текущую стоимость серии равномерных равновеликих поступлений де­нежных средств в течение n-периодов с учетом заданной суммы. Современная величина потока платежей PV — это сумма всех его членов (аннуитетов), уменьшенная (дисконтированная) на величину процентной ставки на конкретный момент времени. Текущая стоимость может быть обычного аннуитета или аван­сового n-периодного аннуитета

где PV - представляет собой сумму я членов геометрической прогрессии со знаменателем 1/1+i и первым членом PMT/1+c

Отсюда, пользуясь известной формулой суммы членов гео­метрической прогрессии, получим уравнение:

Где1 – (1+i)ⁿ / i= F₅ — пятая функция сложного процента, текущая стоимость ' обычного аннуитета.

Авансовый аннуитет построен таким образом, что первый пла­теж РМТ₁ в потоке доходов производится немедленно, а последу­ющие платежи — через равные промежутки времени. Так как РМТ₁ производится в начальный момент времени, дисконтировать его не нужно. Последующий же я — 1 платеж и другие дисконтируют­ся с учетом того, что k-й платеж производится через k — 1 перио­дов от начального момента.

В данном случае сумма стоимости всех n-платежей — это

геометрическая прогрессия со знаменателем 1/1+i и первым чле­ном PMT.

Тогда текущая стоимость авансового аннуитета будет равна:

Если РМТ = 1, то получим выражение для фактора текущей стоимости авансового аннуитета F '₅:

Функции F₅ и F '₅ имеют особое значение в статистических расчетах, в оценке инвестиционных проектов, имущества, при­носящего доход.

Шестая функция сложного процента (обратная к 5-й) в прак­тике экономико-финансовых вычислений имеет название ипо­течная постоянная, или размер платежей для покрытия долга. По известной текущей стоимости (размеру кредита) определя­ется размер платежей:

Для PV = 1 получим значение взноса на амортизацию де­нежной единицы — это и есть шестая функция сложного про­цента — F₆ (ипотечная постоянная).

Для обычных взносов (рента постнумерандо) шестая функ­ция имеет вид:

Для авансовых взносов (рента пренумерандо) шестая функ­ция имеет вид:

Каждый равновеликий взнос РМТ включает сумму процент­ных денег I_nt и уплату первоначальной суммы PRN — суммы основного долга: РМТ= PRN +I_nt

Нужно подчеркнуть, что ипотечная постоянная функция F₆ связана с функцией F₃ следующим образом: F₆=F₃+i т.е. ипотечная постоянная — это взнос на амортизацию капита­ла, равный сумме фактора фонда возмещения F₃ и ставки про­цента на капитал i.

Равномерно-аннуитетный метод возврата основных средств (метод Инвуда). Платежи РМТ идут в конце периода равными долями с увели­чивающимися размерами PRN возврата основной суммы долга и с уменьшающимися начислениями процентов i — доходов.

Равномерно-прямолинейный метод (метод Ринга). Чистый операционный доход равномер­но снижается при постоянной норме возврата основного долга PRN, а доход I _nt равномерно уменьшается. В отличие от метода Ринга метод Инвуда основан на том, что ипотечная постоянная равна сумме фактора фонда возмещения F₃ и ставки капитализации i.

Шестая функция сложного процента широко применяется в экономическом обосновании лизинговых операций.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: