Фактор фонда возмещения капитала.

Третья функция сложного процента (обратная второй) — фак­тор фонда возмещения капитала. Из второй функции имеем:

Где i/ (1+i)ⁿ–1 = F₃ — фактор фонда возмещения, третья функция сложного

процента.

Коэффициент F₃ показывает денежную сумму, которую не­обходимо вносить в конце каждого периода для того, чтобы че­рез определенное число периодов остаток на счете составил одну денежную единицу; причем данный фактор учитывает получае­мый по взносам процент.

Можно сравнить фактор фонда накопления F₂ и фактор фонда возмещения F₃ Видно, что функция F₃ при фиксированных n и i есть величина, обратная фактору фонда накопления F₂ т.е.

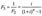
Сравнивая фактор фонда накопления (будущую стоимость авансового аннуитета с платежом в одну единицу) и фактор аван­сового фонда возмещения, получим соотношение:

Размер платежей для покрытия долга – ипотечная постоянная.

Шестая функция сложного процента (обратная к 5-й) в прак­тике экономико-финансовых вычислений имеет название ипо­течная постоянная, или размер платежей для покрытия долга. По известной текущей стоимости (размеру кредита) определя­ется размер платежей:

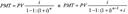
Для PV = 1 получим значение взноса на амортизацию де­нежной единицы — это и есть шестая функция сложного про­цента — F₆ (ипотечная постоянная).

Для обычных взносов (рента постнумерандо) шестая функ­ция имеет вид:

Для авансовых взносов (рента пренумерандо) шестая функ­ция имеет вид:

Каждый равновеликий взнос РМТ включает сумму процент­ных денег I_nt и уплату первоначальной суммы PRN — суммы основного долга: РМТ= PRN +I_nt

Нужно подчеркнуть, что ипотечная постоянная функция F₆ связана с функцией F₃ следующим образом: F₆=F₃+i т.е. ипотечная постоянная — это взнос на амортизацию капита­ла, равный сумме фактора фонда возмещения F₃ и ставки про­цента на капитал i.

Равномерно-аннуитетный метод возврата основных средств (метод Инвуда). Платежи РМТ идут в конце периода равными долями с увели­чивающимися размерами PRN возврата основной суммы долга и с уменьшающимися начислениями процентов i — доходов.

Равномерно-прямолинейный метод (метод Ринга). Чистый операционный доход равномер­но снижается при постоянной норме возврата основного долга PRN, а доход I _nt равномерно уменьшается. В отличие от метода Ринга метод Инвуда основан на том, что ипотечная постоянная равна сумме фактора фонда возмещения F₃ и ставки капитализации i.

Шестая функция сложного процента широко применяется в экономическом обосновании лизинговых операций.

Основные понятия и определения, применяемые в финансовых вычислениях.

Финансовые вычисления – это раздел количественного анализа финансовых операций, предметом которого является изучение функциональных зависимостей между параметрами коммерческих сделок или финансово-банковских операций и разработка на их основе методов решения финансовых задач определённого класса. Финансовые вычисления основаны на учёте фактора времени, что обусловлено принципом неравноценности денег, относящихся к разным моментам времени.

Под процентными деньгами (процентами) понимают абсолютную величину дохода от предоставления денег в долг в любой его форме: выдача ссуды, продажа товара в кредит, помещение денег на депозитный счет, учёт векселя, покупка сберегательного сертификата или облигации и т.д. Какой бы вид или происхождение ни имели проценты, это всегда конкретное проявление такой экономической категории, как ссудный процент.

Под процентной ставкой i понимается относительная величина дохода за фиксированный отрезок времени – отношение дохода (процентных денег) к сумме долга. Процентная ставка – один из важнейших элементов коммерческих, кредитных или инвестиционных контрактов. Она измеряется в виде десятичной или обыкновенной дроби или в процентах.

При помощи процентной ставки может быть определена как будущая стоимость «сегодняшних» денег, так и настоящая (современная, текущая или приведённая) стоимость «завтрашних» денег – например, тех, которыми обещают расплатиться через год после поставки товаров или оказания услуг.

Виды процентных ставок:

простая – применяется к одной и той же первоначальной сумме долга на протяжении всего срока финансовой операции;

сложная – применяется к капитализированной сумме процентов (сумма долга + начисленные проценты);

фиксированная – ставка зафиксирована в виде определённого числа финансовых контрактов;

постоянная – неизменна на протяжении всего срока финансовой операции;

переменная – изменяется во времени, но имеет конкретную числовую характеристику;

плавающая – привязана к определённой величине, изменяющейся во времени, включая надбавку к ней (моржу), которая определяется рядом условий (срок финансовой операции, объём кредита и т.д.).

Размер процентной ставки зависит от ряда как объективных, так и субъективных факторов, а именно: общего состояния экономики, в том числе денежно-кредитного рынка; кратковременных и долгосрочных ожиданий его динамики; вида сделки, её валюты; срока кредита; особенностей заёмщика (его надёжности) и кредитора, истории их предыдущих отношений и т.д.

Временной интервал, к которому приурочена процентная ставка, называют периодом начисления – отрезок времени между двумя следующими друг за другом процедурами взимания процентов. В качестве единицы периода времени принимают год, полугодие, квартал, месяц или даже день. Чаще всего на практике имеют дело с годовыми ставками.

Срок финансовой операции – период времени от начала финансовой операции до её окончания.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: