Дисперсия альтернативного признака.

1.

Основоположником развития теории средних величин является Адольф Кетле, который считал их важнейшими статистическими показателями. Он первым четко сформулировал тот факт, что на массовые явления (статистические совокупности) влияет два вида причин:

- общие для каждой единицы совокупности, эти причины формируют тип явления и связаны с его сущностью;

- индивидуальные, специфические для каждой единицы совокупности, не связанные с типом явления, то есть случайные для него.

При расчете средней величины в совокупности влияние случайных причин взаимопогашается, и средняя величина, абстрагируясь от индивидуальных особенностей отдельных единиц совокупности, выражает общие свойства, присущие всей совокупности. Кетле считал среднюю величину не просто статистическим показателем, имеющим определенный способ расчета, а категорией объективной реальности.

В настоящее время средняя величина признается также центральным показателем, характеризующим совокупность. И определяют ее как обобщающий показатель, характеризующий типический уровень варьирующего признака. Он выражает величину признака, отнесенную к единице совокупности.

Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности.

Вычисление среднего – один из распространенных приемов обобщения; средний показатель выделяет то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае.

Таким образом, в способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Следует отметить, что средняя величина будет объективной характеристикой, если она вычислена по качественно однородной совокупности.

Рассмотрим теперь виды средних величин, особенности их исчисления и области применения. Средние величины делятся на два больших класса: степенные средние и структурные средние.

К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.

В качестве структурных средних рассматриваются мода и медиана.

Выбор конкретного вида средней величины зависит от цели исследования и логической сущности усредняемого признака.

Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.

Простая средняя считается по несгруппированным данным и имеет следующий общий вид:

,

где X – варианта (значение) осредняемого признака;
m – показатель степени средней;
n – число вариант.

В зависимости от степени m получают различные виды средних величин.

Если же данные сгруппированы, то используется формулы средних взвешенных, где весами выступают частоты f (повторяемость варианты).

Взвешенная средня я считается по сгруппированным данным и имеет общий вид

где X – варианта (значение) усредняемого признака или серединноезначение интервала, в котором измеряется варианта;
m – показатель степени средней;
f – частота, показывающая, сколько раз встречается каждое значение усредняемого признака.

Таблица 7. Виды степенных средних

Вид степенной средней	Показатель степени (m)	Формула расчета
Простая	Взвешенная
Гармоническая	-1
Геометрическая
Арифметическая
Квадратическая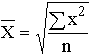
Кубическая

 

Формулы средневзвешенные могут использоваться для расчета общей по совокупности средней на основе групповых средних.

Пример. Рассчитать среднюю заработную плату по двум бригадам.

 

Таблица 8. Оплата труда по бригадам

 

№ бригады	Средняя заработная плата, тыс. руб.	Численность бригады, чел.
Итого	4987,5

 

Таблица 9. Оплата труда по бригадам

№ бригады	Средняя заработная плата, тыс. руб	Фонд заработной платы, тыс.руб.
Итого	4987,5

В обеих задачах определяющей функцией является ФЗП.

Прежде, чем выбрать формулу для расчетов средней величины,нужно словами записать логическую сущность усредняемого признака.

Средняя заработная плата = Фонд заработной платы / численность работников

Средняя урожайность = Валовой сбор / Посевная площадь

Средняя производительность труда = Объем продукции / Численность (Время)

Правило: Если в представленной информации есть данные о числителе логической формулы, то есть об определяющей функции, то для расчета средней величины используется средняя гармоническая. Если представлены данные о знаменателе логической формулы, то для расчета средней величины используется средняя арифметическая.

Пример. В течение 8-часового рабочего дня пять рабочих производили одинаковые детали. Их затраты времени на одну деталь, мин.: 20, 16, 20, 15, 24. Определить средние затраты времени на одну деталь.

Средние затраты времени на одну деталь определяются путем деления суммарного времени на число деталей.

480 +480+480+480+480

480:20+480:16+480:20+480:15+480:24

(2400:130=18,46 мин.)

Это - правильный расчет, а неправильно, если сложить все затраты времени на одну деталь и разделить на пять (19 мин.). При таком расчете искажается объем производства деталей (2400:19=126, а не 130, как фактически).

 

2.

1. Средняя арифметическая постоянной величины равна этой постоянной:

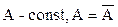
2. Алгебраическая сумма линейных отклонений варианты от средней арифметической равна 0 (нулевое свойство):

– для несгруппированных данных,

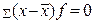– для сгруппированных данных;

3. Сумма квадратов отклонений варианты от средней арифметической есть число минимальное:

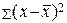– min (для несгруппированных данных),

– min (для сгруппированных данных);

Эти три свойства определяют сущность средней арифметической. Следующие свойства – расчетные.

4. Если каждую варианту Х уменьшить или увеличить на определенное число, то средняя величина уменьшается или увеличивается на это число.

5. Если каждую варианту Х уменьшить или увеличить в одно и то же число раз, то средняя величина уменьшается или увеличивается в это число раз.

6. Если каждую частоту f уменьшить или увеличить в одно и то же число раз, то средняя величина не изменится.

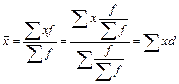
Доля каждой варианты (d) определяется путем деления каждой частоты на сумму всех частот.

Таким образом средняя величина зависит от варианты Х и от структуры совокупности, которая характеризуется долями d.

7. Средняя суммы равна сумме средних:

 

 

3.

Ряд распределения имеет 3 центра:

1) средняя арифметическая;

2) мода;

3) медиана.

Рассчитаем среднюю арифметическую для дискретного ряда распределения, представленного в таблице 1:

При расчете средней величины по интервальному ряду распределения в качестве варианты Х берется середина интервала. Если интервал открытый, то при расчете средней величины его условно закрывают, принимая равным соседнему закрытому интервалу.

Рассчитаем среднюю величину основных средств по таблице 3:

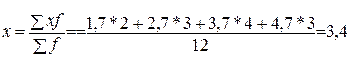млрд.руб.

В таблице 5 была рассчитана эта же величина, и она получилась равной 3,3 млрд. руб. (Объяснить различия)

Мода – наиболее часто встречающаяся варианта.

Определим моду тарифного разряда по таблице 1:

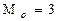
Для интервальных рядов распределения сначала находится модальный интервал, то есть интервал с наибольшей частотой внутри этого интервала, затем мода находится по формуле:

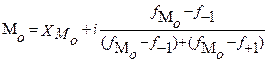
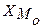- нижняя граница модального интервала;

i - величина модального интервала;

- частота модального интервала;

- частота интервала предшествующего модальному интервалу;

-- частота интервала следующего за модальным интервалом.

 

млрд. руб.

 

Медиана - варианта, стоящая в середине ряда распределения.

 

Номер медианы:

№ Ме= - если число единиц в совокупности четное;

№ Ме= - если число единиц в совокупности нечетное.

Найдем медиану тарифного разряда по таблице 1:

№ Ме=

Ме=3

Следовательно, половина рабочих цеха имеет разряд не выше 3-го.

 

Прежде чем найти медиану для интервального ряда распределения, ищут интервал, в который входит срединная варианта, затем внутри этого интервала определяют медиану по формуле:

,

где - нижняя граница медианного интервала;

i- величина медианного интервала;

n- число единиц совокупности;

- накопленная частота интервала предшествующего медианному;

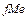- частота медианного интервала

 

Найдем медиану основных средств по таблице 3:

№ Ме=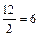

млрд.руб.,

То есть половина предприятий имеет основные средства не выше, чем 3,45 млрд. руб.

 

4.

Ряды распределения, имеющие одинаковую среднюю величину, могут существенно отличаться по степени колеблемости изучаемого признака. (Пример. Средний возраст студентов в группе и бабушки с детьми).

Для характеристики совокупности, особенно, в том случае, если значение признака существенно колеблется, дополнительно к расчету средней величины определяют ряд показателей вариации.

Для измерения вариации используют абсолютные и относительные показатели.

1. Размах вариации: R = X _max – X _min – диапазон изменения признака.

2. Среднее линейное отклонение – показывает среднее отклонение варианты от средней величины:

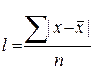- для несгруппированных данных;

- для сгруппированных данных;

3. Среднее квадратическое отклонение - показывает среднее отклонение вариант от средней величины:

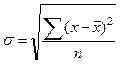- для не сгруппированных данных;

- для сгруппированных данных;

Все 3 показателя имеют те же единицы измерения, что и признак.

 

4. Дисперсия – квадрат среднего квадратического отклонения:

или

Не имеет единиц измерения.

Свойства дисперсии:

1) D(const)=0, то есть дисперсия постоянной величины равна 0.

2) Если каждую варианту Х уменьшить или увеличить на одно и то же число раз, то дисперсия не изменится;

3) Если каждую варианту Х уменьшить или увеличить в одно и то же число раз i, то дисперсия уменьшится или увеличится в i ² раз.

 

Способы расчета дисперсии:

1) исходя из определения:

2) исходя из средней из квадратов вариант:

; ;

 

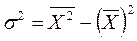Эта формула получена преобразованием основной формулы.

3) по способу моментов:

- первый условный момент;

- второй условный момент;

;

 

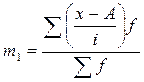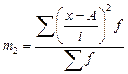
Рассчитаем дисперсию тарифного разряда по данным таблицы 1 двумя способами:

 

1)

 

2) =13,75-3,53=1,29

 

Показатели относительного рассеивания (вариации).

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер вариации в различных распределениях (колеблемость одного и того же признака в двух совокупностях или колеблемость различных признаков в одной совокупности). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической.

1. Коэффициент осцилляции показывает относительную колеблемость крайних значений признака относительно средней.

2. Относительное линейное отклонение характеризует относительное усредненное значение абсолютных отклонений от средней величины.

3. Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.

В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.

Для более глубокого анализа колеблемости признаков также используют показатели дифференциации.

1. По несгруппированным первичным данным можно рассчитать коэффициент фондовой дифференциации:

,

где - средняя величина, рассчитанная для 10% самых больших значений признака.

- средняя величина, рассчитанная для 10% самых маленьких значений признака.

2. Если данные сгруппированы, то рассчитывают коэффициент децильной дифференциации:

, где и - соответственно 1 и 9 децили.

Дециль - значение признака, которому в ряду распределения соответствует 10-я доля совокупности, то есть децили делят совокупность на 10 равных частей..

Процедура нахождения децилей аналогична процедуре нахождения медианы для интервального ряда распределения:

1) определяют № децили: для 1-й децили: № = ;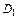

для 9-й децили: № = ;

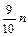2) находят интервалы, в которые входят эти децили и внутри этих интервалов находят децили по формулам:

; ,

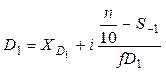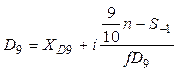где и - соответственно нижние границы интервалов, в которые входят 1 и 9 децили;

i - величины интервалов, в которые входят 1 и 9 децили;

и - соответственно частоты интервалов, в которые входят 1 и 9 децили;

- накопленная частота интервала, предшествующая децильному (в первой формуле для 1-й децили, во второй формуле для 2-й децили).

Таблица 10. Распределение населения района

По среднедушевому доходу

Месячный среднедушевой доход, тыс.руб	Численность	Накопленные частоты
тыс.чел.	в % к итогу
20-40 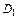- 40-60 60-100 100-150 150-200 - 200-300 300-500 500 и выше	9,2 25,2 32,9 30,0 27,4 15,5 4,9 3,1	6,2 17,0 22,2 20,2 18,5 10,5 3,3 2,1	9,2 () 34,4 (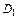) 67,3 97,3 124,7 () 140,2 () 145,1 148,2
Итого	148,2		-

 

№ =

№ =

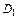- max доход для 10% самого бедного населения;

- min доход для 10% самого богатого населения.

(min доход самого богатого населения больше max дохода самого бедного населения в 5,8 раз).

 

5.

На колеблемость результативного признака оказывает влияние множество факторных признаков (пример с успеваемостью студентов в группе).

Одной из задач статистики является определение влияния какого-либо факторного признака на колеблемость результативного признака. Всю колеблемость результативного признака измеряют т.н. общей дисперсией результативного признака.

,

Х – варианта результативного признака;

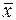- средняя величина результативного признака, рассчитанная по всей совокупности;

n – число единиц совокупности.

Для того чтобы установить влияние какого-то одного факторного признака на колеблемость результативного признака проводят аналитическую группировку по этому факторному признаку.

Результативный признак колеблется внутри каждой выделенной группы под влиянием других факторных признаков, которые не положены в основу аналитической группировки. Эту колеблемость измеряют с помощью внутригрупповой дисперсии:

,

i -номер группы;

- внутригрупповая средняя результативного признака;

f_i - число единиц в группе.

 

Для того чтобы определить колеблемость результативного признака под влиянием колеблемости других признаков по всей совокупности рассчитывают среднюю из этих внутригрупповых дисперсий.

.

Групповые средние колеблются вокруг общей средней. Эту колеблемость измеряют с помощью межгрупповой дисперсии:

.

Межгрупповая дисперсия показывает колеблемость результативного признака под влиянием колеблемости факторного признака, по которому проводили аналитическую группировку. Т.о., всю колеблемость результативного признака разделили на 2 части:

1) колеблемость результативного признака под влиянием изучаемого факторного признака (меряется межгрупповой дисперсией);

2) колеблемость результативного признака под влиянием всех других факторных признаков (меряется средней из внутригрупповых дисперсий):

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: