 |
Сущность рядов динамики и их виды.
|
|
|
|
Аналитические показатели динамических рядов.
Средние характеристики динамических рядов.
Смыкание динамических рядов и приведение их к одному основанию.
Выравнивание динамических рядов.
Выявление сезонных колебаний.
Интерполяция и экстраполяция уровней динамических рядов.
1.
В предыдущих темах мы научились рассчитывать различные статистические показатели, но не учитывали, что они меняются во времени. Если рассчитать, например, среднюю зарплату за ряд лет, то получим ее динамический ряд. Таким образом возникает одна из важнейших статистических задач – составление и анализ рядов динамики, которые характеризуют развитие социально – экономических явлений во времени.
Ряд статистических показателей, расположенных в хронологической последовательности, называют рядом динамики или временным рядом.
 |
|
|
|
|
Период времени
 | |||
 | |||
интервальный
ряд динамики
Рис. 1. Виды рядов динамики
Уровень моментного ряда динамики характеризует состояние какого-то явления на определённую дату, а уровень интервального ряда динамики характеризует итог развития какого-то явления за определённый период времени.
Следует иметь в виду, что моментные ряды могут быть построены из абсолютных и относительных величин, а интервальные ряды – из любых величин. Уровни интервальных рядов, построенных из абсолютных величин, можно суммировать (производство продукции по годам), для моментных же рядов сумма уровней даже из абсолютных величин не имеет смысла (численность студентов).
|
|
|
При построении динамических рядов возникает проблема сопоставимости их уровней.
Уровни динамического ряда должны быть сопоставимы, т.е. однородны по своему содержанию за разные периоды времени или на разные моменты времени.
Однако существует ряд причин, которые нарушают сопоставимость уровней. Основные причины следующие:
1. Различный охват единиц совокупности, по которым рассчитываются уровни динамического ряда (пример со средним баллом: стационар + заочники).
2. Различная методология расчётов статистических показателей (пример с производством электроэнергии).
3. Цены (Большинство экономических показателей стоимостные, и постоянный рост цен приводит к несопоставимости уровней динамических рядов).
Основные задачи статистического анализа рядов динамики:
1. Характеристика интенсивности изменения уровней рядов динамики. Эта задача решается с помощью системы аналитических показателей (второй вопрос темы).
2. Обобщающая характеристика динамики явления. Эта заача решается с помощью расчета средних показателей рядов динамики (третий вопрос темы).
3. Выявление основных закономерностей динамики явления. Для решения этой задачи используют различные методы выравнивания (четвертый вопрос).
4. Прогноз развития явления. Существует множество методов прогноза, то есть экстраполяции выявленной закономерности развития (Простейшие – пятый вопрос).
2.
Аналитические показатели динамических рядов рассчитываются путём сопоставления уровней динамического ряда. Назначение этих показателей - охарактеризовать интенсивность изменения уровней динамического ряда.
Сравнение уровней динамического ряда может проводиться двумя способами: цепным и базисным.
При цепном способе сравнения каждый уровень сравнивается с предыдущим и получают цепные аналитические показатели или показатели с переменной базой сравнения.
|
|
|
При базисном способе сравнения каждый уровень динамического ряда сравнивается с базисным уровнем (обычно начальный уровень ряда) и полученные таким способом показатели называются базисными или показателями с постоянной базой сравнения. Введем обозначения.
Уровни динамического ряда – у0, у1, у2,…,уn
y0 – базисный уровень
при цепном способе у0, у1, у2,…,уn
при базисном у0, у1, у2,…,уn
Чаще всего рассчитывают следующие аналитические показатели:
1. Абсолютный прирост или абсолютное отклонение.
2. Темп роста.
3. Темп прироста (относительное отклонение).
4. Абсолютное содержание 1% прироста.
Рассмотрим названные показатели.
Абсолютный прирост – разность уровней динамического ряда. Он показывает, на сколько единиц своего измерения изменился статистический показатель.
Цепной абсолютный прирост - это разница между каждым последующим и каждым предыдущим уровнями ряда.
Базисный абсолютный прирост – это разница между каждым последующим уровнем ряда и уровнем, принятым за базу сравнения.
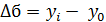
Сумма цепных приростов даёт последний базисный прирост.
Темп роста – отношение уровней динамического ряда, следовательно, он показывает, во сколько раз изменился статистический показатель. Темпы роста могут выражаться в коэффициента и в процентах.
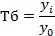
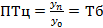(последний)
Произведение цепных темпов роста (П) даёт темп роста базисный последний.
Темп прироста – отношение абсолютного прироста (цепного или базисного) к предыдущему или базисному уровню, т.е. это относительное отклонение, которое показывает, на сколько процентов изменился статистический показатель.
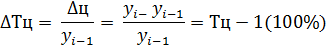
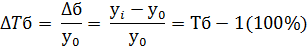
Абсолютное содержание 1% прироста – отношение абсолютного цепного прироста к цепному темпу прироста, выраженному в %, т.е. он показывает, сколько «стоит» 1% прироста.
Таблица 15 – Динамика производства электроэнергии в Республике Беларусь
| Показатели | 2008 г. | 2009 г. | 2010 г. |
| 1 Производство электроэнергии, млрд. кВт/ч | 31,2 | 33,1 | 32,7 |
| 2 Абсолютное отклонение, млрд. кВт/ч | |||
| - к предыдущему году | - | 1,9 | -0,4 |
| - к 2008 г. | 1,9 | 1,5 | |
| 3 Темп роста, % | |||
| - к предыдущему году | - | 10,1 | 98,8 |
| - к 2008 г. | 100,0 | 106,1 | 104,8 |
| 4 Темп прироста, % | |||
| - к предыдущему году | - | 6,1 | -1,2 |
| - к 2008 г. | 6,1 | 4,8 | |
| Абсолютное содержание 1% изменения, млрд. кВт/ч | 0,312 | 0,331 |
|
|
|
В 2010 г. производство электроэнергии в Республике Беларусь выросло по сравнению с 2008 г. на 1,5 млрд.квт-час или 4,8%, однако по сравнению с 2009 г. оно снизилось на 0,4 млрд.квт-час или 1,2%. 1% снижения составляет 0,331млрд.квт-час.
3.
Для обобщения рядов динамики рассчитывают их средние характеристики. Можно выделить две группы таких характеристик:
1. Средние уровни динамического ряда.
2. Средние аналитические показатели динамического ряда.
Рассмотрим расчёт показателей первой группы.
Расчёт среднего уровня зависит от вида динамического ряда. Для интервальных рядов с равными периодами времени средний уровень рассчитывается по формуле средней арифметической простой:
Для интервальных рядов с неравными периодами времени используется среднеарифметическая взвешенная.
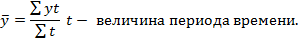
Для моментных рядов с равностоящими датами средний уровень ряда рассчитывается по средней хронологической.
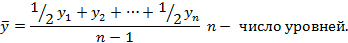
Для моментных рядов с неравноотстоящими датами используют среднюю арифметическую взвешенную.
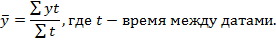
Пример. На 1 января стоимость основных средств составила 7,5 млрд. рублей. В марте введено основных средств на сумму 1,2 млрд. рублей. В мае их выбыло на 0,7 млрд. рублей. В сентябре ввели основные средства на 0,8 млрд. рублей. Определить среднегодовую стоимость основных средств.
Построим ряд динамики моментный:
| Даты | млрд. рублей. |
| 1.1 | 7.5 |
| 1.4 | 8.7 |
| 1.6 | 8.0 |
| 1.10 | 8.8 |
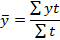
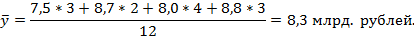
Теперь рассмотрим расчёт показателей второй группы, т.е. средних аналитических показателей.
Средний абсолютный прирост рассчитывается по формуле средней арифметической простой из цепных абсолютных приростов.
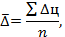
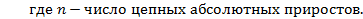
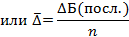
По таблице 15 рассчитаем среднегодовой абсолютный прирост
Т.е. в среднем за год производство электроэнергии приросло на 0,75 млрд. квт-ч.
Средний темп роста рассчитывается по формуле средней геометрической из цепных темпов роста.
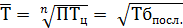, где n – число цепных темпов роста, ПТц – произведение темпов роста.
|
|
|
По таблице 15 считаем средний темп роста
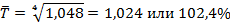
Если нужно рассчитать средний темп роста для интервального ряда с разными периодами времени, то используют среднегеометрическую взвешенную:
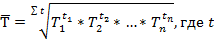- величина периода времени.
Пример. Средний темп роста производства продукции за 2 года составлял 104,5%, за следующие 3 года 107,9%. Определить средний темп роста за 5 лет.
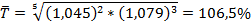
Средний темп прироста
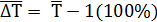
По таблице 17 среднегодовой темп прироста составляет 2,4%
4.
Одной из задач анализа рядов динамики является установление закономерности изменения уровней изучаемого явления. Чаще всего можно говорить об общей тенденции развития явления. Выявление такой тенденции развития и называют выравниванием динамического ряда (достаточно часто тенденцию развития называют trend). При выравнивании считают, что все факторы, влияющие на уровни динамического ряда, можно выразить через время и считать тем самым, что у=f(t), где у - уровень динамического ряда, а t - время.
Рассмотрим 3 наиболее часто используемые метода выравнивания:
1. Укрупнение интервалов динамического ряда
2. Метод скользящей средней
3. Аналитическое выравнивание
При первом методе от исходных рядов динамики переходят к новым рядам динамики с более крупными интервалами. Например, от месячных данных можно перейти к квартальным данным, от квартальных данных можно перейти к годовым данным и т.д. При таком подходе случайные колебания погашаются, и тенденция развития просматривается более ярко.
При втором методе также от исходного ряда динамики переходят к новому ряду, который состоит из средних величин, рассчитанных по уровням исходного ряда. При применении этого метода удобнее интервал для расчёта средней величины составить из нечётного числа интервалов. Чем длиннее исходный динамический ряд, тем больше может быть этот интервал. При этом нужно учитывать, что новый динамический ряд будет короче исходного ряда на n-1 уровней, где n – число уровней исходного ряда, принятых при расчёте скользящей средней.
Рассмотрим этот метод на примере (см. табл.16 и рис.2)
При третьем методе не только предполагает, что уровень динамического ряда есть функция от времени, но и стоят эту функцию у=f(t), которую называют трендовая модель. При построении этой модели используют различного вида простые функции.
Например, линейную, параболу, гиперболу, показательную функцию, экспоненту и др.
Выбор вида функции важен, так как от него зависит точность последующего прогноза по трендовой модели. Обычно выбор функции осуществляется на основе графика исходного динамического ряда или графика динамического ряда, выравненного более простыми методами.
|
|
|
Таблица 16. Динамика удельного расхода условного топлива на производство теплоэнергии на ТЭЦ.
| Годы | Удельный расход, кг./Гкал | Скользящие средние, кг./Гкал | t | Y выравненный, кг./Гкал |
| 171,8 | - | -9 | 169,0 | |
| 167,6 | 168,4 | -7 | 168,6 | |
| 165,8 | 166,9 | -5 | 168,3 | |
| 167,4 | 167,1 | -3 | 168,0 | |
| 168,0 | 167,6 | -1 | 167,6 | |
| 167,5 | 167,6 | 167,3 | ||
| 167,2 | 167,1 | 167,0 | ||
| 166,5 | 166,7 | 166,6 | ||
| 166,5 | 166,5 | 166,3 | ||
| 166,4 | - | 166,0 | ||
| Итого | 1674,7 | - | - | 1674,7 |
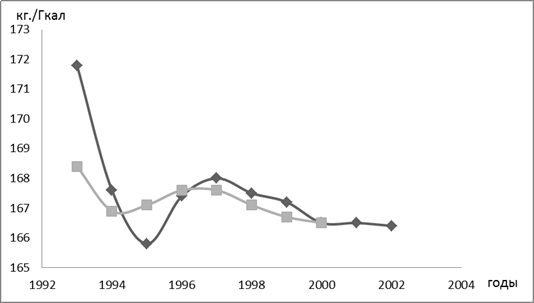
Рис.2. Динамика удельного расхода условного топлива
Параметры трендовой модели находятся методом наименьших квадратов. (Сущность этого метода рассмотрена в теме «Статистическое изучение связи между признаками»).
Рассмотрим аналитическое выравнивание по прямой, то есть y=a0+a1t, где t - порядковый номер уровня динамического ряда. В соответствии с методом наименьших квадратов параметры а0,а1 находятся из следующей системы нормальных уравнений:
Если динамический ряд имеет разные интервалы, то расчёт параметров трендовой модели можно упростить, преобразовав динамический ряд таким образом, что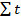 
=0, где t -порядковый номер.
Для этого перенумеруем уровни динамического ряда следующим образом: если число уровней нечётное, то уровню, стоящему в середине ряда присваивают номер 0, выше стоящим уровням присваивают номера -1, -2; ниже стоящим уровням 1, 2, 3 и т.д. Если число уровней четное, то срединной паре присваивают номера -1, 1; выше стоящим номера- -3, -5, -7 и т.д., а ниже стоящим 3, 5, 7 и т.д. В этом случае система нормальных уравнений преобразуется таким образом:
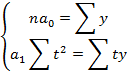
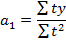
Проведём аналитическое выравнивание с помощью линейной функции, по таблице 18 рассчитаем величины а0 и а1
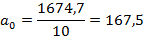
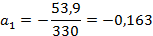
y=167,5-0,163t– удельный расход снижался в среднем за полугодие на 0,163 кг.
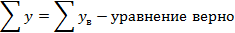
у1993выр=167,5-0,163*(-9)=169,0 и т.д., занесём в таблицу 16 и определим
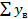=1674,7.
Построить на рис. График трендовой модели.
5.
Под сезонными колебаниями понимают закономерные внутригодичные изменения, то есть устойчиво повторяющиеся из года в год колебания уровней динамического ряда.
Существует несколько способов выявления сезонных колебаний, достаточно простым и в то же время надёжным, является построение индексов сезонности. Для стабильных динамических рядов, то есть для рядов без ярко выраженной тенденции к росту или падению, индекс сезонности рассчитывается по формуле.
Рассмотрим расчёт этих индексов на следующем примере.
Таблица 17. Число расторгнутых браков населением города.
| месяцы |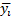 
| |||||
| I | 165,7 | 122,4 | 22,4 | |||
| II | 147,0 | 108,6 | 8,6 | |||
| III | 150,7 | 111,3 | 11,3 | |||
| IV | 136,0 | 100,4 | 0,4 | |||
| V | 136,0 | 100,4 | 0,4 | |||
| VI | 125,7 | 92,8 | -7,2 | |||
| VII | 126,0 | 93,1 | -6,9 | |||
| VIII | 120,7 | 89,1 | -10,9 | |||
| IX | 87,2 | -12,8 | ||||
| X | 94,5 | -5,5 | ||||
| XI | 131,7 | 97,3 | -2,7 | |||
| XII | 139,3 | 102,9 | 2,9 | |||
| 131,8 | 135,6 | 138,7 | 135,4 |
На основании отклонений от индекса сезонности строится сезонная волна, которая наглядно показывает сезонные колебания.
Рис.3. Сезонная волна числа расторгнутых браков в городе
Обобщающим показателем силы сезонных колебаний является среднее квадратическое отклонение индексов сезонности.
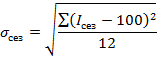
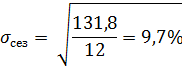
То есть среднее отклонение от среднего уровня составляет 9,7%.
Для динамических рядов с выраженной тенденцией к росту или падению ряда индексы сезонности рассчитывают следующим образом:
1. Проводят аналитическое выравнивание динамического ряда по какой-то трендовой модели.
2. Рассчитывают по трендовой модели у выравненные, то есть теоретические уровни динамического ряда.
3. Рассчитывают отношения фактических уровней динамического ряда к теоретическим.
4. Для каждого месяца рассчитывают индексы сезонности таким образом:
6.
Интерполяция - определение недостающих уровней динамического ряда внутри ряда. Самым простым способом интерполяции является расчёт средней из уровней, между которыми лежит недостающий уровень.
Экстраполяция – нахождение уровней динамического ряда за его пределами. Экстраполяция – продление выявленной закономерности изменения уровней. По существу экстраполяция – один из методов прогноза. Наиболее простым методом экстраполяции является использование среднего абсолютного прироста или среднего темпа роста.
Определим производство электроэнергии в 2011 году, используя таблицу 15.
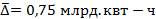
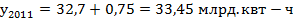
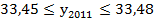
Более точным и обоснованным методом экстраполяции является экстраполяция, основанная на аналитическом выравнивании.
Проведём экстраполяцию по данным таблицы 16.
Для экстраполяции используем построенную трендовую модель.
Для того, чтобы определить доверительный интервал для точечного прогноза определяют среднеквадратическое отклонение от тренда.
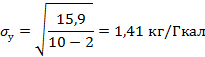
Кроме среднеквадратического отклонения величина доверительного интервала зависит от уровня задаваемой вероятности, который определяет значение критерия Стьюдента. При вероятности p(t)=0.95 и числе степеней свободы =8, (n-m=10-2) величина критерия Стьюдента по таблице=2,306.
Величина доверительного интервала будет равна t* 
=2,306*1,41=3,25 кг/Гкал.
|
|
|
