 |
Определенный интеграл. Вычисление площадей плоских фигур.
|
|
|
|
Липецк-2019
Комплект контрольно-измерительных материалов по учебной дисциплине ЕН.01 Элементы высшей математики разработан на основе Федерального государственного образовательного стандарта среднего профессионального образования по специальности 09.02.01 Компьютерные системы и комплексы
Организация разработчик: ГОАПОУ СПО «Липецкий металлургический колледж»
Разработчики:
Афанасьева Л.Н., преподаватель математических дисциплин
| Одобрено Председатель цикловой комиссии математических и общих естественнонаучных дисциплин | Согласовано Заместитель директора по учебной работе | |
| Л.Н.Красникова | Н.М. Левина |
Введение
Методические указания по выполнение контрольной работы составлены в соответствии с содержанием рабочей программы учебной дисциплины «Элементы высшей математики» (дисциплина входит в математический и общий естественнонаучный учебный цикл учебного плана специальности 09.02.01 Компьютерные системы и комплексы
Контрольная работа направлены на овладение следующими знаниями и умениями.
уметь:
- вычислять пределы;
- находить производною сложной функции;
- вычислять интегралы различными методами;
-находить частные производные нескольких действительных переменных;
- находить экстремум функции нескольких действительных переменных;
знать:
-основные математического анализа;
-дифференциальное исчисление функции одной переменной;
- интегральное исчисление функции одной переменной;
- дифференциальное исчисление функции нескольких действительных переменных;
Методические указания по проведению контрольной работы содержат теоретическую часть, который кратко представляет основной материал, необходимый для освоения коммуникативных умений и знаний; контрольные задания.
|
|
|
При выполнении контрольной работы необходимо соблюдать следующие правила:
1. Работа выполняется в отдельной тетради(12листов).
(Контрольная работа №1
По дисциплине: «Математика»
студента(ки) группы (свою группу)
по специальности (код специальности)
ФИО)
2. Условие задачи записывается полностью.
3. Решения задачи должны сопровождаться краткими, но достаточными объяснениями. Для решения выбирать оптимальный вариант.
4. Проверенные работы сохраняются и предоставляются на зачете.
5. Студент должен ознакомиться с рецензией преподавателя и дать объяснения по всем замечаниям.
6. Если работа не зачтена, то ее необходимо переделать и сдать на повторную рецензию.
7. Основной материал изучается по учебникам.
Глава 1. Математический анализ.
Предел функции.
1. Определение. Таблица замечательных пределов.
Обозначения: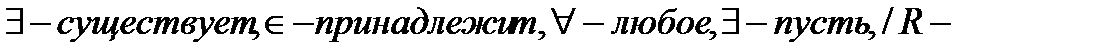 
множество вещественных чисел.
Опр. 1.1. 
, допустим, что каждому значению 
по какому – либо закону поставлено в соответствие 
. Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.
Обозн. 
Пример.
Пусть 
определена в некоторой окрестности точки а.
Опр. 1.2. число b называется пределом функции при 
, если для любой последовательности аргументов 
сходящихся к а, соответствующая последовательность значений функций 
сходится у b.
Обозн. 
Таблица пределов:
Свойства пределов:
1) 
;
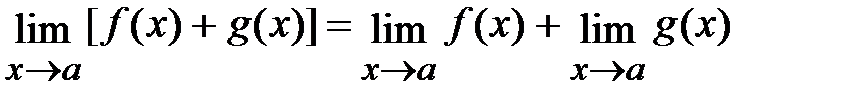2) 
;
3) 
;
4) 
(при 
).
Пример. Вычислить предел.
1.2. Производная функции.
1. Непрерывность функции.
Опр. 2.1. Функция 
называется непрерывной в точке а, если она имеет предел 
и этот предел равен значению функции в этой точке, т.е. 
|
|
|
Пусть функция у = f(x) определена на промежутке X. Возьмем точку х 
Х. Дадим значению х приращение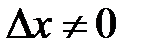 
, тогда функция получит приращение 
.
Опр. 2.2. Производной функции у = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
.
Пример.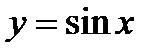 
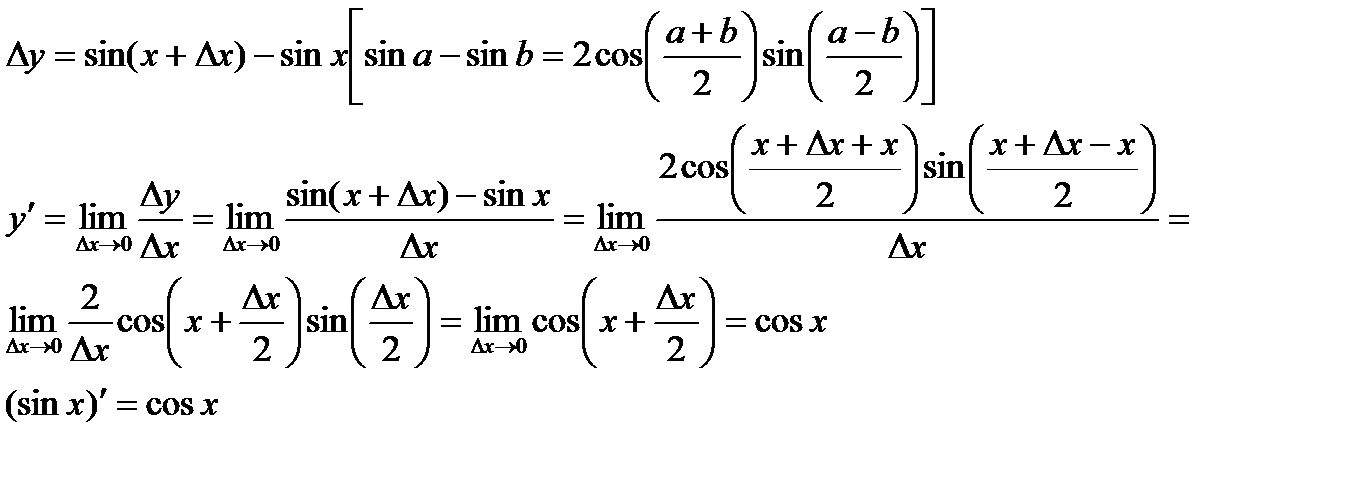
Таблица производных:
1. 
.
2. 
.
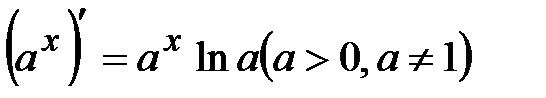3. 
.
4. 
.
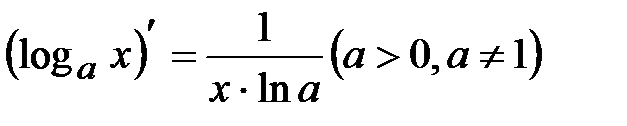5. 
.
6. 
.
7. 
.
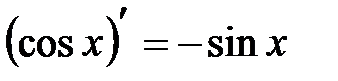8. 
.
9. 
.
10. 
.
11. 
.
12. 
.
13. 
.
Свойства производных:
Если С - постоянное число, 
- функции, имеющие производные, тогда:
(I);
(II);
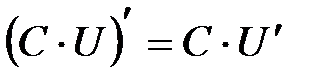(III);
(IV);
(V).
Пример. Вычислить производную функций.
1.3. Производная сложной функции.
Исследование функции с помощью производной.
Пусть 
композиция двух функций.
Т.3.1. Если функция 
дифференцируема по x, а функция 
дифференцируема по y, то сложная функция 
дифференцируема по x, причем её производная вычисляется по формуле: 
Пример. 
Интегральное исчисление
1. Первообразная функции
Опр. 4.1.
Функция F(x) над первообразной функции F(x) на некотором промежутке, если для всех x из этого промежутка 
Пр: 1) F(x)=sin x – первообр. F(x)=cosx, т.к. 
2) 
- первооб. 
,т.к 
.
Задача Док – ть, что F(x) – первооб. F(x)
1. 
3. 
2. 
4. 
1.5 Неопределенный 
. Его свойства.
Опр. 5.1. Интегрирование – это процесс нахождения первообразованых
Опр. 5.2. Множество первообразованых для данной функции F(x) над неопределенным интегралом и обозначается 
Пр. 
Таблица неопределенных интегралов
1. 
.
2. 
.
3. 
.
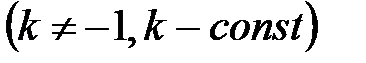4. 
.
5. 
.
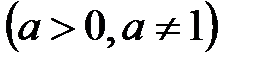6. 
.
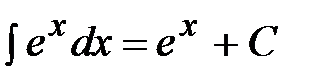7. 
.
8. 
.
9. 
.
10. 
.
11. 
.
12. 
.
13. 
.
14. 
Свойства неопределенного интеграла:
1. Если 
– постоянная величина, то 
.
2. 
3. 
.
4. 
.
5. 
.
Задача: Вычислить неопределенный интеграл.
Определенный интеграл. Вычисление площадей плоских фигур.
Опр.6.1. Фигура, ограниченная снизу отрезком 
оси ох, сверху
графиком функции 
, с боков отрезками х=а, х= b,
называется криволинейной трапецией.
|
|
|
Площадь криволинейной трапеции вычисляется по формуле:
Таким образом, вычисление площади криволинейной трапеции сводится к отысканию первообразной F (x) функции , т.е. к интегрированию F (x).
Опр. 6.2. Разность 
называется интегралом от функции F (x) и обозначается 
.
- формула Ньютона – Лейбница.
Пример. Найти площадь фигуры, ограниченной графиком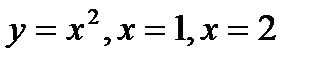 
Свойства определенного интеграла аналогичны свойствам неопределенного интеграла.
|
|
|
