 |
Метод замены переменной (метод подстановки).
|
|
|
|
Существует три метода вычисления интегралов: непосредственное интегрирование, метод замены переменной, метод интегрирования по частям.
Пример.
Частные производные
Дана функция двух переменных Z=F(x,y),дадим аргументу x приращение Bx, а арг. Y менять не будем, Т.Е. перейдем от точки с координатами (x,y) к точке с координатоми (x+bx,y).
Тогда функция F(x,y) получит приращение 
,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
Опр.10.1: 
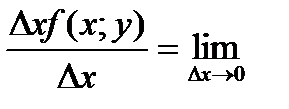
Он над частной производной ф-ии
F(x,y) и обозн. 
Аналогична опред-ся ч.пр. F(x,y) по Y
Т.Е ч.пр. 
это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр 
это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
Пр; Найти ч.пр. ф-ии 
Пример 1
Исследовать на экстремум функцию
Решение: на первом шаге нужно отыскать стационарные точки. Для этого найдём частные производные 1-го порядка:
Контроль: 
и решим систему:
В данном случае получена система двух линейных уравнений с двумя неизвестными, которую можно решить несколькими способами. Но мудрить здесь не надо – как проще, так и решаем. Из 2-го уравнения выразим 
и подставим в 1-е уравнение:
Таким образом: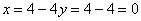 
– стационарная точка. Тут, главное, не перепутать координаты.
Выполним промежуточную проверку:
Достаточное условие экстремума функции двух переменных,
для применения которого нужно вычислить частные производные 2-го порядка в точке 
Для компактности обычно используют следующие обозначения:
Если 
, то функция 
имеет экстремум в точке , причём, если 
, то это минимум, а если 
– то максимум.
Примечание: здесь также можно ориентироваться и на букву «цэ», т.к. неравенство выполняется только в том случае, если 
и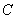 
– одного знака.
|
|
|
Если 
, то в точке нет экстремума.
Если же 
, то требуется дополнительное исследованиеВ нашем примере все частные производные 2-го порядка равны константам:
а значит, соответствующим константам они равны и в частности в точке :
Таким образом: 
, следовательно, в точке 
есть экстремум, и так как , то это – минимум. Осталось его найти. Перепишем функцию 
, чтобы она была перед глазами, и ОЧЕНЬ внимательно проведём вычисления:
Надо сказать, момент весьма неприятный, поскольку здесь существует ненулевая вероятность запороть всё задание. Правда, в данном случае вычисления здОрово облегчил нулевой «икс».
Ответ: 
ГОАПОУ «Липецкий металлургический колледж»
| Рассмотрено МОЕНД | Обязательная контрольная работа №2 | Утверждаю Заместитель директора по учебной работе |
| по учебной дисциплине «Элементы высшей математики» | ||
| «____» __________ 20____г. | специальность 09.02.01 Компьютерные системы и комплексы | |
| Председатель _________________ | «_________20__г. |
Вариант №1
1.Вычислить пределы
1) 
|
2)  
|
3) 
|
2.Найти производные данных функций.
· 
;
· 
;
3.Найти интегралы.
· 
· 
· 
4.Вычислить площадь фигуры ограниченной линиями.
5. а) Найти частные производные первого и второго порядков;
б) найти частные производные первого порядка:
a) U= x2 +2y2 -3xy-4x+2y+5,
б) U=sin(x2+y2).
6.Найти экстремума функции двух переменных
| ||
|
Преподаватель ________________ Афанасьева Л.Н.
ГОАПОУ «Липецкий металлургический колледж»
| Рассмотрено МОЕНД | Обязательная контрольная работа №2 | Утверждаю Заместитель директора по учебной работе |
| по учебной дисциплине «Элементы высшей математики» | ||
| «____» __________ 20____г. | специальность 09.02.01 Компьютерные системы и комплексы | |
| Председатель _________________ | «_________20__г. |
|
|
|
Вариант №2
1.Вычислить пределы
2) 
|
2) 
|
3) 
|
2.Найти производные данных функций.
· 
;
· 
;
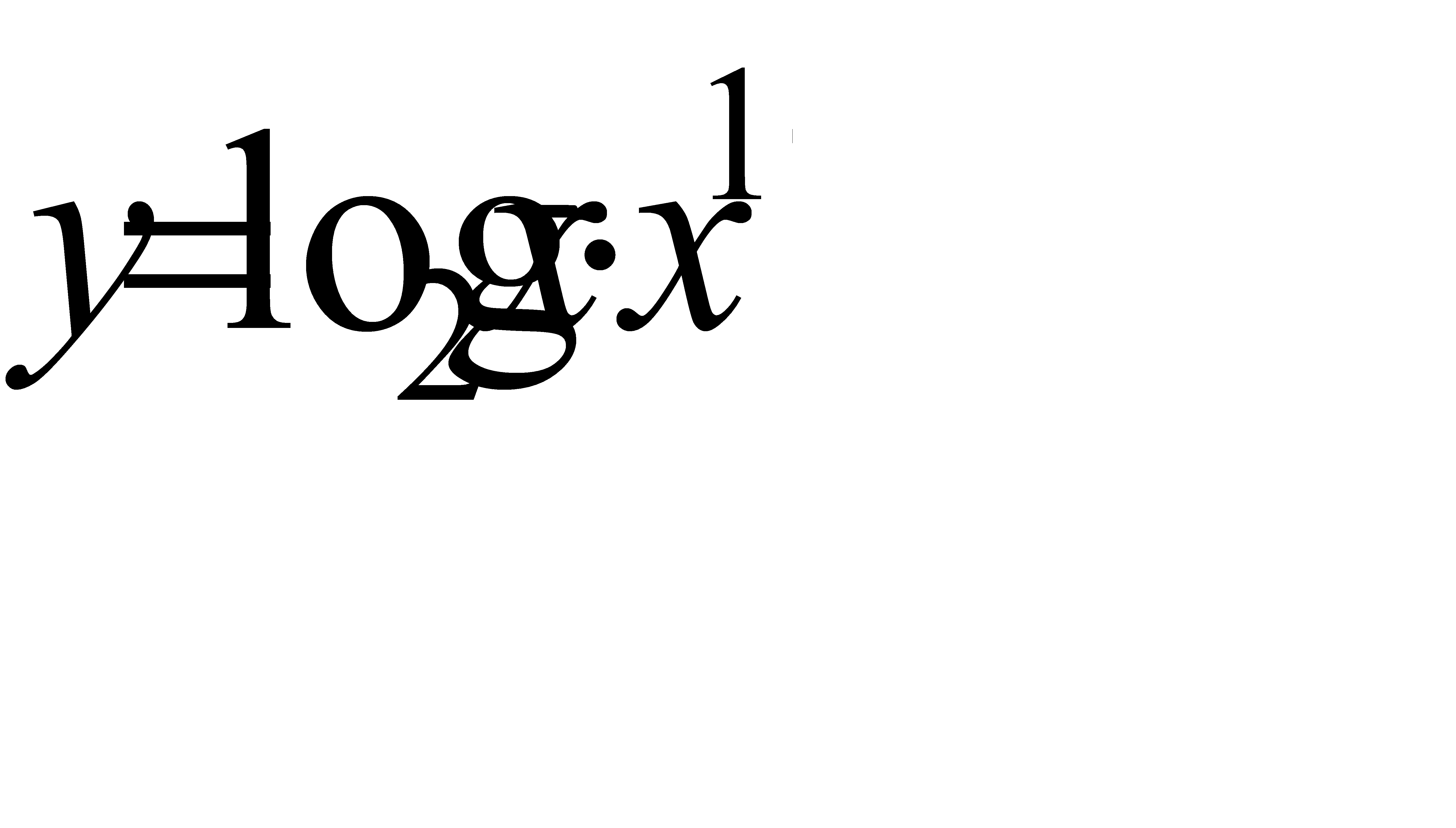3.Найти интегралы.
· 
· 
· 
4.Вычислить площадь фигуры ограниченной линиями.
5. а) Найти частные производные первого и второго порядков;
б) найти частные производные первого порядка:
a) U= 3x2 +y2 -3xy+2y+5,
б) U=cos(x2+y2).
7.Найти экстремума функции двух переменных
|
Преподаватель ________________ Афанасьева Л.Н.
|
|
|
