 |
Основные композиции движений пространства
|
|
|
|
Предисловие
Композиции геометрических преобразований пространства являются логическим продолжением темы композиций геометрических преобразований плоскости. И если последние освещены в литературе сравнительно полно, то для пространства литературы гораздо меньше.
Целью данной работы является рассмотрение и изучение некоторых композиций преобразований евклидова пространства. Эти композиции выбирались следующим образом: строился стереометрический аналог для некоторых теорем, задач из планиметрии (планиметрические задачи можно найти в [2]), решались задачи из [3].
В настоящей работе рассмотрены и систематизированы 14 композиций преобразований евклидова пространства, оформленные в виде задач, поэтому эта работа может быть использована при проведении факультативных занятий в школе для детей с подходящим уровнем знаний и на первых курсах ВУЗов в курсе геометрии.
Введение
Пусть f и g – два преобразования множества X такие, что f (x)= y, g (y)= z для произвольного x Î X, конечно, y Î X и z Î X. Отображение j определим законом j (x)= g (f (x)). Тогда отображение j является преобразованием множества X и называется композицией (произведением) преобразований f и g. В литературе принято следующее обозначение композиции преобразований: j = g ◦ f.
Композиции преобразований обладают следующими свойствами:
1 °. Композиция преобразований ассоциативна, т. е. для любых преобразований f, g, h данного множества имеет место равенство:
h ◦(g ◦ f)=(h ◦ g)◦ f.
2 °. Композиция преобразований антикоммутативна, но в частных случаях композиции преобразований могут быть коммутативными.
В дальнейшем будут рассматриваться композиции преобразований евклидова пространства.
|
|
|
Композиции движений пространства
Основные композиции движений пространства
Рассмотрим композиции движений пространства, которые часто используются при нахождении других композиций движений и при решении геометрических задач.
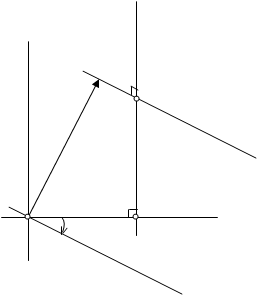
Задача 1. Найти композицию поворота Rl j и переноса  пространства при условии, что вектор
пространства при условии, что вектор 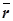 и ось поворота l не параллельны.
и ось поворота l не параллельны.
Решение. Представим оба движения композициями осевых симметрий:
Rl j = Sb ◦ Sa, где a ^ l, b ^ l, Ð (a, b) =  (здесь и дальше будут рассматриваться ориентированные углы), a Ç b Ç l = O и
(здесь и дальше будут рассматриваться ориентированные углы), a Ç b Ç l = O и  = Sv ◦ Su, где u ║ v, u ^
= Sv ◦ Su, где u ║ v, u ^ 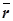 . Пользуясь имеющимся произволом в выборе осей симметрий, можно совместить оси u и b (рис. 1). Тогда
. Пользуясь имеющимся произволом в выборе осей симметрий, можно совместить оси u и b (рис. 1). Тогда  ◦ Rl j = Sv ◦ Su ◦ Sb ◦ Sa = Sv ◦ Sa. Если вектор
◦ Rl j = Sv ◦ Su ◦ Sb ◦ Sa = Sv ◦ Sa. Если вектор 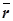 не ортогонален оси l, то прямые a и v скрещиваются, и угол между ними равен углу между a и b, т.е. равен
не ортогонален оси l, то прямые a и v скрещиваются, и угол между ними равен углу между a и b, т.е. равен 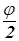 . Композиция Sv ◦ Sa есть винтовое движение с осью m, являющейся общим перпендикуляром прямых a и v, и вектором 2
. Композиция Sv ◦ Sa есть винтовое движение с осью m, являющейся общим перпендикуляром прямых a и v, и вектором 2 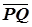 , где P = a Ç m, Q = v Ç m, m ║ l. Итак,
, где P = a Ç m, Q = v Ç m, m ║ l. Итак,
 ◦ Rl j =
◦ Rl j = 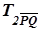 ◦ Rl j , m ║ l.
◦ Rl j , m ║ l.
Если 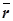 ^ l, прямые a и v пересекаются, поэтому
^ l, прямые a и v пересекаются, поэтому 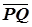 =
=  , и искомая композиция является поворотом Rm j . Если при этом j = p, то имеем, что
, и искомая композиция является поворотом Rm j . Если при этом j = p, то имеем, что  ◦ Rl j = Sm,
◦ Rl j = Sm,  ^ l, m ║ l.
^ l, m ║ l.
|
|
|
|
|
|
| |||||
|
|
|
|
| m |
|
| |||||
|
| l |
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
| Q |
|
|
|
| ||||
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
| v | ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| P |
| a |
| ||||
|
| O |
|
| u |
|
| |||||
|
|
| b |
|
|
|
Рис. 1
|
|
|
Задача 2. Найти композицию двух поворотов пространства Rb b ◦ Ra a.
Решение. Сначала найдём композицию Rb b ◦ Ra a двух поворотов, оси которых скрещиваются. Построим общий перпендикуляр h прямых a и b и представим заданные повороты композициями осевых симметрий:
Ra a = Sh◦Su , Rb b =Sv◦Sh , u ^ a, u ^ b, u Ç h Ç a=A, v Ç h Ç b=B,
Ð (u, h) =  , Ð (h, v) =
, Ð (h, v) = 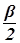 (рис. 2). Тогда
(рис. 2). Тогда
Rb b ◦ Ra a = Sv ◦ Sh ◦ Sh ◦ Su = Sv ◦ Su. Оси u и v скрещиваются, если бы они принадлежали одной плоскости, то прямые a и b, перпендикулярные этой плоскости, были бы параллельны. При таком расположении осей полученная композиция симметрий Sv ◦ Su есть винтовое движение, осью которого является общий перпендикуляр l прямых u и v, угол w =2 Ð (u, v), а вектор  = 2
= 2 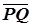 , где P = u Ç l, Q = v Ç l.
, где P = u Ç l, Q = v Ç l.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| b |
|
| h |
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| a |
| B |
|
| v |
|
| u ¢ |
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| A |
|
|
|
| l |
| u |
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2
Угол w винтового движения можно вычислить через углы a и b данных поворотов и угол g = 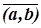 . По теореме косинусов для трехгранного угла с вершиной B, ребрами которого являются лучи h, u ¢, v, справедливо следующее равенство:
. По теореме косинусов для трехгранного угла с вершиной B, ребрами которого являются лучи h, u ¢, v, справедливо следующее равенство:
cos 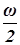 = - cos
= - cos 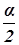 cos
cos 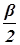 - sin
- sin 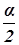 sin
sin 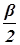 cos g (доказательство данной формулы можно найти в [4], с. 26).
cos g (доказательство данной формулы можно найти в [4], с. 26).
Рассмотрим случай, когда оси a и b пересекаются (в точке B). Тогда прямые u и v также будут пересекаться в точке B, и u ¢ совпадет с прямой u. Искомая композиция Rb b ◦ Ra a есть поворот R l w, причем угол этого поворота подсчитывается по указанной выше формуле. При a ║ b и a + b ¹ 2 p прямые u и v пересекаются в точке O. И рассматриваемая композиция Rb b ◦ Ra a есть поворот R l a + b, ось l которого проходит через точку O параллельно прямым a и b.
|
|
|
При a║ b и a + b=2 p будет u ║ v. В этом случае композиция поворотов является переносом.
Задача 3. Найти композицию трех зеркальных симметрий.
Решение. Выделим случай, когда композиция трех зеркальных симметрий является зеркальной симметрией, S g ◦ S b ◦ S a = S w. Это равенство эквивалентно равенству S b ◦ S a = S g ◦ S w. Если плоскости a и b имеют общую прямую l, то S b ◦ S a = Rl j и поэтому S g ◦ S w = Rl j. Следовательно, все четыре плоскости имеют общую прямую l. Если же плоскости a и b параллельны, то S b ◦ S a = 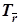 и S g ◦ S w =
и S g ◦ S w = 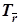 . Следовательно, все четыре плоскости параллельны.
. Следовательно, все четыре плоскости параллельны.
Нетрудно доказать обратное. Таким образом, если плоскости зеркальных симметрий пересекаются по одной прямой или параллельны, то их композиция является зеркальной симметрией, плоскость которой соответственно содержит прямую пересечения или параллельна плоскостям, исходных симметрий.
Пусть плоскости a, b, g имеют единственную общую точку O. В этом случае она является единственной неподвижной точкой композиции этих симметрий (предположение о существовании другой неподвижной точки приводит к предыдущему случаю). Следовательно, композиция f = S g ◦ S b ◦ S a есть поворотная симметрия. Найдем ее компоненты: плоскость, ось и угол поворота. Обозначим прямые пересечения плоскостей следующим образом: b Ç g = a, g Ç a = b, a Ç b = c (рис. 3).
Пусть f (c)= c 1, тогда прямые c и c 1 симметричны относительно плоскости g, и S a (a)= a 0, тогда f (a 0)= a. Поскольку плоскость w поворотной симметрии f делит каждый отрезок, соединяющий соответственные точки, пополам, то ей принадлежат ортогональные проекции m и n прямых a и c соответственно на плоскости a и g. Итак, w есть плоскость, проходящая через прямые m и n. Ось l поворота есть перпендикуляр к плоскости w в точке O, угол поворота j равен углу между ортогональными проекциями a 0 и a (или c и c 1) на плоскость w.
|
|
|
|
|
|
|
|
| O |
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
| c |
|
|
|
|
| a |
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| c1 |
|
|
|
| |||
| a0 |
|
|
| m |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
| w |
| b | n |
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3
Если плоскости a, b, g попарно перпендикулярны, то искомая композиция является центральной симметрией Zo.
Рассмотрим случай, когда плоскости a, b, g исходных симметрий попарно пересекаются по параллельным прямым, т.е. a ║ b ║ c. Тогда в каждой плоскости, перпендикулярной этим прямым, композиция f = S g ◦ S b ◦ S a индуцирует композицию осевых симметрий относительно прямых пересечения этой плоскости с плоскостями a, b, g. А она является переносной симметрией рассматриваемой плоскости с определенными осью l и вектором  . Поэтому, учитывая род композиции, композиция f есть переносная симметрия пространства с вектором
. Поэтому, учитывая род композиции, композиция f есть переносная симметрия пространства с вектором 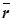 и плоскостью, проходящей через прямую l параллельно прямым a, b, c.
и плоскостью, проходящей через прямую l параллельно прямым a, b, c.
|
|
|




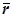
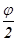























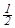 b
b a
a