 |
Композиции подобий и аффинных преобразований пространства
|
|
|
|
Среди преобразований пространства выделяют также преобразования, не сохраняющие расстояния между точками, - это подобия, гомотетии как частный случай подобий, и аффинные преобразования.
Задача 13. Найти композицию гомотетии и переноса пространства: 
◦ HOk.
Решение. Рассмотрим образ произвольной точки X после применения искомой композиции. Пусть X 1 – образ X после применения HOk: HOk (X)= X 1, а точка X 2 – образ X 1 после применения переноса: 
(X 1)= X 2. Через центр гомотетии O проведем прямую n параллельную прямой, содержащую вектор 
(рис. 13).
|
| S1 |
| S | O | |||||||||
| X | |||||||||||||
| X1 |
| X2 |
Рис. 13
Найдем образ точки пересечения построенной прямой n и прямой XX 2 при гомотетии HOk: HOk (S)= S 1. Тогда 
= , поэтому точка S при заданной композиции неподвижна, кроме того, не зависит от выбора точки X. С учетом того, что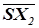 
= k 
, 
= k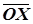 
(т.к. треугольники SOX и X 1 XX 2 подобны), искомая композиция является гомотетией HSk.
Таким образом, ◦ HOk = HSk. (4)
Задача 14. Найти композицию двух гомотетий пространства.
Решение. Рассмотрим образ произвольной точки X после применения композиции гомотетий f = HBm ◦ HAk. Пусть HAk(X)= X 1, т.е. по определению гомотетии 
= k 
, HBm (X 1)= X 2, т.е. 
= m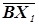 
(рис.14). Найдем образ точки A после применения гомотетии HBm: HBm (A)= A 1, т.е. 
= m 
. Таким образом, отрезок A 1 X 2 – это образ отрезка AX после применения данной композиции, при этом прямые, содержащие эти отрезки параллельны (это следует из подобия треугольников ABX 1 и A 1 BX 2). Если прямые AA 1 и XX 2 пересекаются (обозначим точку их пересечения C), тогда, рассматривая подобные треугольники ACX и A 1 CX 2 , выразим вектор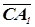 
:
|
|
|
= 
= 
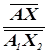, при этом 
= m 
= km .
| X2 | |||||||||||
| A1 | ||||||||||||
| C | ||||||||||||
| B | ||||||||||||
| A | ||||||||||||
| X | ||||||||||||
| X1 |
Рис. 14
Следовательно, 
= km 
. Точка C не зависит от выбора точки X, значит композиция f является гомотетией с центром в C:
HBm ◦ HAk = HCkm. (5)
Если прямые AA 1 и XX 2 не пересекаются, т.е. 
= 
, то km =1, следовательно, композиция f есть перенос пространства:
HBm ◦ HAk = . (6)
Все эти рассуждения верны и для совпадающих центров исходных гомотетий.
Задача 15. Найти композицию двух подобий пространства.
Решение. Так как любое подобие пространства можно представить в виде композиции поворота и гомотетии, центр которой лежит на оси поворота, то, учитывая ассоциативность этого представления, будем находить требующуюся композицию в следующем виде: f = HBm ◦ Rh b ◦ Rl a ◦ HAk.
Рассмотрим несколько случаев.
1)Если оси поворотов h и l параллельны, и при этом сумма углов не равна 2 p, то композиция поворотов является поворотом Rn a + b, где ось n параллельна исходным осям h, l. Тогда f = HBm ◦ Rn a + b ◦ HAk, при этом композиция Rn a + b ◦ HAk является по определению подобием, а значит, эта композиция может быть представлена в виде HDk ◦ Rp a + b. И равенство f = HBm ◦ Rn a + b ◦ HAk эквивалентно равенству f = HBm ◦ HDk ◦ Rp a + b. По формуле (5) HBm ◦ HDk = HCkm (при km ¹ 1), значит f = HCkm ◦ Rp a + b, а это по определению подобие. При km = 1 по формуле (6) HBm ◦ HDk = , и f = ◦ Rp a + b, а это, в общем случае, винтовое движение.
|
|
|
2)Если же при параллельных осях данных поворотов h и l сумма углов равна 2 p, то композиция поворотов Rh b ◦ Rl a является переносом пространства , и в этом случае f = HBm ◦ ◦ HAk. Композиция ◦ HAk согласно выводу (4)есть гомотетия с центром в некоторой точке C с коэффициентом k: ◦ HAk = H С k. Следовательно, f = HBm ◦ H С k, а это гомотетия пространства (согласно формуле (5)) или параллельный перенос пространства (по (6)).
3)Если прямые h и l пересекаются, то композиция поворотов Rh b ◦ Rl a является поворотом Rn w. И нахождение композиции f сводится к случаю 1.
4)Если оси h и l скрещиваются, то композиция поворотов Rh b ◦ Rl a является винтовым движением, следовательно, композиция Rh b ◦ Rl a ◦ HAk является подобием пространства, которое можно представить композицией поворота и гомотетии: Rh b ◦ Rl a ◦ HAk = Rn w ◦ H С n. Тогда нахождение f сводится к случаю 1.
Таким образом, композиция двух подобий пространства, произведение коэффициентов которых не равно 1, есть подобие пространства или гомотетия (в случае параллельных осей поворотов и сумме их углов 2 p), в тривиальном случае, когда произведение коэффициентов исходных подобий равно 1, эта композиция может вырождаться в винтовое движение пространства или перенос.
Аналогичная ситуация обстоит и с композицией аффинных преобразований пространства, т.е. в общем случае композиция двух аффинных преобразований пространства также является аффинным преобразованием.
Литература
1. Гусев В. А., Тхамафокова С. Т. Преобразования пространства. Москва: «Просвещение», 1979.
2. Понарин Я. П. Геометрия: Учебное пособие. Ростов-на-Дону: «Феникс», 1997.
3. Понарин Я. П. Преобразования пространства. Киров: 2000.
4. Скопец З. А. Геометрические миниатюры. Москва: «Просвещение», 1990.
|
|
|
