|
Композиции осевых симметрий пространства
|
|
|
|
Задача 9. Композиция трех осевых симметрий пространства является осевой симметрией: Sc ◦ Sb ◦ Sa = Sl. Какое взаимное положение могут иметь прямые a, b, c? Построить ось l этой композиции в каждом из возможных случаев.
Решение. Равенству Sc ◦ Sb ◦ Sa = Sl эквивалентно равенство
Sc◦Sb=Sl◦Sa . (*)
Если прямые b и c параллельны, то Sc ◦ Sb = 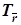 . Тогда и правая часть равенства (*) является переносом: Sl ◦ Sa =
. Тогда и правая часть равенства (*) является переносом: Sl ◦ Sa = 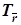 . А значит прямые a и l также будут параллельными.
. А значит прямые a и l также будут параллельными.
Таким образом, получили, что, если прямые b, c параллельны, то все оси a, b, c и l попарно параллельны (рис. 9а).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| h |
|
| l |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| A |
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
| |||||||||||
| c |
| b |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
| l |
|
|
|
|
|
|
|
|
|
|
| O |
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| c |
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
|
| a |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| b |
|
Рис. 9а Рис. 9б
Если прямые b и c пересекаются в точке O, то композиция Sc ◦ Sb является поворотом Rh j (см. [3], c. 15), где h – перпендикуляр к плоскости, проходящей через прямые b и c, при этом точка O принадлежит оси h, угол j = 2 Ð (b, c)(рис. 9б). Тогда и композиция Sl ◦ Sa является этим же поворотом Rh j, значит h – перпендикуляр к плоскости, проходящей через прямые a и l, точка пересечения A которых принадлежит оси h, и ориентированный угол между a и l равен углу поворота j.
Таким образом, если оси b и c пересекаются, то прямая a параллельна плоскости, проходящей через b и c, пересекается с перпендикуляром h к этой плоскости, восстановленным в точке пересечения прямых b и c. Ось l удовлетворяет следующим условиям:точка пересечения A прямых a и h принадлежит l, l параллельна плоскости (b, c), ориентированные углы Ð (a, l) = Ð (b, c). Если точка A принадлежит прямой a, то точки A и O совпадают, т.е. ось l также походит через точку A.
Если прямые b и c скрещиваются, то композиция Sc ◦ Sb является винтовым движением Rh 2 j ◦ 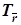 , ось h которого есть общий перпендикуляр к прямым b и c, вектор
, ось h которого есть общий перпендикуляр к прямым b и c, вектор  коллинеарен оси h, угол j равен ориентированному углу между прямыми b и c (рис. 9в). В силу равенства (*) композиция Sl ◦ Sa является этим же самым винтовым движением: Sl ◦ Sa = Rh 2 j ◦
коллинеарен оси h, угол j равен ориентированному углу между прямыми b и c (рис. 9в). В силу равенства (*) композиция Sl ◦ Sa является этим же самым винтовым движением: Sl ◦ Sa = Rh 2 j ◦ 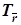 , то есть h – общий перпендикуляр к скрещивающимся прямым a и l, и угол Ð (a, l) = j.
, то есть h – общий перпендикуляр к скрещивающимся прямым a и l, и угол Ð (a, l) = j.
| h |
|
|
| l |
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
| a |
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
| c |
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
| b |
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9в
Таким образом, если оси b и c - скрещивающиеся, то прямые a, b и c попарно скрещиваются и имеют общий перпендикуляр h. Ось l удовлетворяет следующим условиям: l и h - перпендикулярные прямые, расстояния между прямыми b, c и a, l равны, и углы между этими осями также равны.
Обобщая все рассмотренные случаи, получаем, что композиция трех осевых симметрий является осевой симметрией, если исходные оси либо попарно параллельны, либо попарно скрещиваются и имеют общий перпендикуляр, либо лежат в параллельных плоскостях по две, пересекаются, и прямая, проведенная через точки пересечения, является для осей общим перпендикуляром.
Задача 10. Композиция трех осевых симметрий есть перенос: Sc ◦ Sb ◦ Sa = 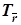 . Каково взаимное положение их осей?
. Каково взаимное положение их осей?
Решение. Если прямые b и c параллельны, то композиция Sc ◦ Sb является переносом 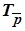 . Тогда
. Тогда 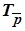 ◦ Sa =
◦ Sa = 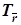 , полученное равенство эквивалентно равенству Sa =
, полученное равенство эквивалентно равенству Sa = 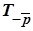 ◦
◦ 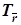 или Sa =
или Sa = 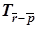 (этот факт легко доказывается по аналогии с композицией переносов в планиметрии, см. [2], с. 308). Это равенство противоречиво, а значит композиция Sc ◦ Sb ◦ Sa при параллельных b и c не может быть переносом.
(этот факт легко доказывается по аналогии с композицией переносов в планиметрии, см. [2], с. 308). Это равенство противоречиво, а значит композиция Sc ◦ Sb ◦ Sa при параллельных b и c не может быть переносом.
Если прямые b и c пересекаются в точке O, то композиция Sc ◦ Sb является поворотом Rh j, где h – перпендикуляр к плоскости, проходящей через прямые b и c, при этом точка O принадлежит оси поворота h, и угол j =2 Ð (b, c). Тогда исходная композиция Sc ◦ Sb ◦ Sa = 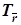 будет эквивалентна следующей композиции Rh j ◦ Sa =
будет эквивалентна следующей композиции Rh j ◦ Sa = 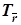 . Такое возможно только, если поворот Rh j является осевой симметрией пространства, т.е. угол j = ± p, при чем оси симметрий a и h параллельны, и расстояние между ними равно
. Такое возможно только, если поворот Rh j является осевой симметрией пространства, т.е. угол j = ± p, при чем оси симметрий a и h параллельны, и расстояние между ними равно 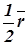 . В силу этих рассуждений, получили, что ось a перпендикулярна плоскости (b, c), а прямые b и c перпендикулярны между собой.
. В силу этих рассуждений, получили, что ось a перпендикулярна плоскости (b, c), а прямые b и c перпендикулярны между собой.
|
|
|
Таким образом, при пересекающихся осях b и c для выполнения исходного равенства необходимо, чтобы прямые a, b и c были попарно перпендикулярными.
Если b и c скрещиваются, то композиция Sc ◦ Sb является винтовым движением Rh j ◦ 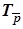 , где h – общий перпендикуляр прямых b и c, угол j =2 Ð (b, c),
, где h – общий перпендикуляр прямых b и c, угол j =2 Ð (b, c),  =
=  (рис. 10).
(рис. 10).
|
|
| h |
|
|
|
|
|
|
|
|
| ||||
|
|
| |||||||||||||||
|
|
|
|
| B |
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
| b |
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| c |
|
|
|
| ||||
|
|
|
| C |
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10
Следовательно, Sc ◦ Sb ◦ Sa = 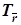 эквивалентно равенству Rh j ◦
эквивалентно равенству Rh j ◦ 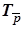 =
= 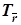 ◦ Sa. А это возможно, если угол j = ± p, и прямые a и h параллельны, иначе говоря прямая a перпендикулярна b и c. Т.е. исходное равенство при скрещивающихся прямых b и c возможно, если все три оси взаимно перпендикулярны.
◦ Sa. А это возможно, если угол j = ± p, и прямые a и h параллельны, иначе говоря прямая a перпендикулярна b и c. Т.е. исходное равенство при скрещивающихся прямых b и c возможно, если все три оси взаимно перпендикулярны.
Таким образом, композиция трех осевых симметрий пространства есть перенос, если оси этих симметрий попарно перпендикулярны.
|
|
|