Делимость многочленов. Свойства делимости

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

НАБЕРЕЖНОЧЕЛНИНСКИЙ ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МАТЕМАТИКИ И МЕТОДИКИ ЕЕ ПРЕПОДАВАНИЯ

АЛГОРИТМЫ С МГНОГОЧЛЕНАМИ

/дипломная работа/

Набережные Челны

Год

Содержание

 

Введение

1. Многочлены

2. Деление многочленов

2.1. Делимость многочленов. Свойства делимости

2.2. Деление многочленов с остатком

2.3. Наибольший общий делитель многочленов

2.4. Алгоритм Евклида

3. Кратные корни

4. Производная от многочлена

5. Кратные множители

5.1. Выделение кратных множителей

Заключение

Список использованной литературы

Введение

Тема моей дипломной работы: «Алгоритмы с многочленами».

Целью данной работы является изучение многочленов, алгоритмов с ними, рассмотрение возможностей составления различных программ. Для достижения поставленной цели необходимо рассмотреть следующие вопросы:

– делимость многочленов;

– деление многочленов с остатком;

– наибольший общий делитель, алгоритм Евклида;

– кратные корни;

– кратные множители, выделение кратных множителей;

– производные от многочленов.

Для выполнения дипломной работы я поставила следующие задачи:

1. изучить литературу о многочленах;

2. применить теорию высшей алгебры в решении задач элементарной математики;

3. составить программы для нахождения частного и остатка при делении многочленов, наибольшего общего делителя двух многочленов, производной многочлена; разложения многочленов на кратные множители.

Многочлены

 

Общий вид уравнения n-ной степени (где n некоторое положительное число) есть

.                                                                     (1.1)

Коэффициенты  этого уравнения мы будем считать произвольными комплексными числами, причем старший коэффициент  должен быть отличным от нуля.

Если написано уравнение (1.1), то всегда предполагается, что требуется его решить, найти такие числовые значения для неизвестного x, которые удовлетворяют этому уравнению, то есть после подстановки вместо неизвестного и выполнения всех указанных операций обращают левую часть уравнения (1.1) в нуль.

Целесообразно заменить задачу решения уравнения (1.1) более общей задачей изучения левой части этого уравнения

,                                                                      (1.2)

называемой многочленом n -ной степени от неизвестного х. Многочленом называется лишь выражение вида (1.2), то есть лишь сумма целых неотрицательных степеней неизвестного x, взятых с некоторыми числовыми коэффициентами. В частности, мы не будем считать многочленами такие выражения, которые содержат неизвестное x с отрицательными или дробными показателями. Для сокращенной записи многочленов употребляются символы f (x), g (x) и так далее.

Деление многочленов

 

Теория многочленов в определенном отношении похожа на теорию целых чисел, хотя внешне эти две теории не имеют ничего общего. Внутренняя же близость, схожесть этих теорий объясняется тем, что для многочленов, так же как и для целых чисел, можно определить деление и, что еще более важно, деление с остатком.

Делимость многочленов. Свойства делимости

Многочлен  делится на многочлен , если существует такой многочлен , что выполняется равенство

                                                                                   (2.1)

Например, из равенства   следует, что делится на многочлен и на многочлен .

Многочлен  в равенстве (2.1) определяется однозначно. Если бы существовал многочлен , удовлетворяющий равенству (2.1), то мы получили бы, что

                                                               (2.2)

откуда

Но многочлен  по условию ненулевой, и в силу утверждения или  нулевом является многочлен , т.е. многочлен совпадает с .

Многочлен  в равенстве (2.1) называется частным от деления  на , а  – делителем.

Укажем некоторые основные свойства делимости многочленов.

1. Если  делится , а  делится на , то  будет делиться на .

В самом деле, по условию   и , а поэтому .

2. Если  и  делятся на , то их сумма и разность также делятся на .

Из равенств  и  вытекает .

3. Если  делится на , то произведение  на любой многочлен  также будет делиться на .

Если , то .

Из 2. и 3. вытекает следующее свойство:

4. Если каждый из многочленов 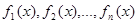 делится на , то на  будет делиться и многочлен , где  - произвольные многочлены.

5. Всякий многочлен  делится на любой многочлен нулевой степени.

Если , а с - произвольное число, не равное нулю, то есть произвольный многочлен нулевой степени, то .

6. Если  делится на , то  делится и на с , где с – произвольное число отличное от нуля.

Из равенства  следует равенство .

7. Многочлены 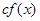, , и только они будут делителями многочлена , имеющими такую же степень, что и .

Действительно, . То есть  делится на .

Если  делится на , причем степени  и 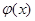 совпадают, то степень частного от деления  на  должна быть равной нулю, то есть , , откуда .

Отсюда вытекает следующее свойство:

8. Тогда и только тогда многочлены ,  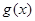одновременно делятся друг на друга, если , .

Из 1. и 8. вытекает свойство:

9. Всякий делитель одного из двух многочленов , , где , будет делителем и для другого многочлена.

Свойства делимости многочленов могут быть применены для изучения делимости в множестве целых чисел. Выясним, например, для каких целых чисел n число является простым.

Натуральное число, отличное от 1, называется простым, если оно делится только на 1 и на само себя; целое отрицательное число k называется простым, если число –k простое.

Для ответа на поставленный вопрос заметим, что справедливо равенство

                                               (2.3)

и поэтому число делится на  и на  Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств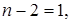

Остается проверить следующие значения n: 3, 1, 0, -3, -1 и –2. При этих значениях n рассматриваемое число равно соответственно 19, -5, 3, 4, так что искомое множество чисел есть

Может возникнуть вопрос: откуда взялось равенство (2.3)? Как мы догадались, что многочлен  таким образом раскладывается на множители? Для нахождения разложений такого типа необязательно прибегать к искусственным группировкам, это можно сделать с помощью теории, которая будет изложена ниже.

Из этого примера видно, что уже для решения задач, связанных с делимостью целых чисел, полезно уметь выяснять, делится ли данный многочлен на некоторый другой многочлен (раскладывается ли на множители).Ответ на такой и многие другие вопросы можно найти с помощью деления многочлена с остатком.

123	Поделиться:

Воспользуйтесь поиском по сайту: