 |
Выделение кратных множителей
|
|
|
|
Если дан многочлен 
с разложением (5.2) и если через 
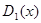мы обозначим наибольший общий делитель 
и его производной 
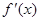то (5.3) будет разложением для 
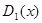. Деля (5.2) на (5.3), мы получим:
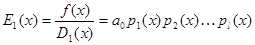
т.е. получим многочлен, не содержащий кратных множителей, причем всякий неприводимый множитель для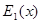 
, имеющего вообще говоря, меньшую степень и, во всяком случае, содержащего лишь простые множители. Если эта задача для 
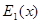будет решена, то останется определить лишь кратность найденных неприводимых множителей в 
, что достигается применением алгоритма деления.
Усложняя изложенный сейчас метод, можно сразу перейти к рассмотрению нескольких многочленов без кратных множителей, причем, найдя неприводимые множители этих многочленов, мы не только найдем все неприводимые множители для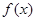 
, но и будем знать их кратность.
Пусть (5.2) будет разложением на неприводимые множители, причем наивысшая кратность множителей есть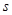 
, 
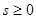. Обозначим через 
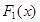произведение всех однократных множителей многочлена 
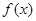, через 
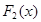- произведение всех двукратных множителей, но взятых лишь по одному разу, и т.д., наконец 
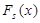- произведение всех 
-кратных множителей, также взятых лишь по одному разу; если при этом для некоторого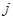 
в отсутствуют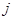 
-кратные множители, то полагаем 
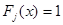. Тогда будет делиться на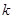 
- тую степень многочлена 
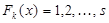и разложение (5.2) примет вид
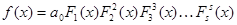
а разложение (5.3) для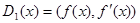 
перепишется в виде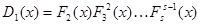 
обозначая через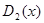 
наибольший общий делитель многочлена 
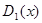и его производной и вообще через 
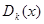наибольший общий делитель многочленов 
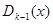и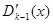 
, таким путем получим:
……………………………
.
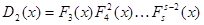
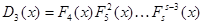
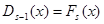
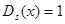Отсюда
,
……………………………
,
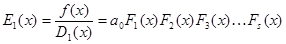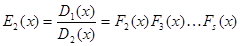
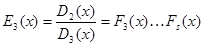
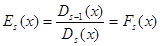И поэтому, наконец,
, 
, …, 
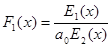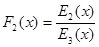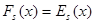
Таким образом, пользуясь лишь приемами, не требующими знания неприводимых множителей многочлена 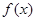, а именно взятием производной, алгоритмом Евклида и алгоритмом деления, мы можем найти многочлены 
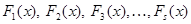без кратных множителей, причем всякий неприводимый множитель многочлена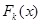 
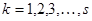, будет 
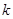-кратным для 
.
|
|
|
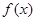Пример. Разложить многочлен на кратные множители.
│ 
│ 
│ 
│ 
│ 
│ 
│ 
│ 
│
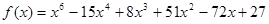
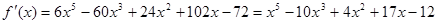
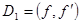
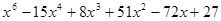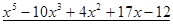
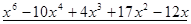
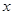
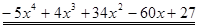
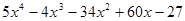
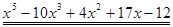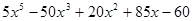
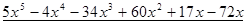
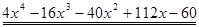
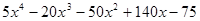
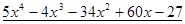
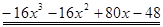
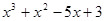
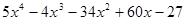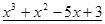
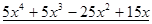
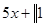
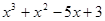
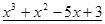
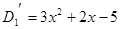
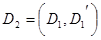
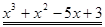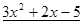
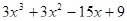
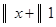
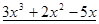
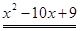
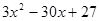
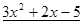
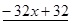
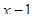
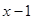
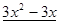
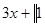
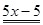
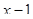
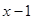
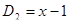
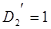
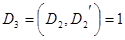
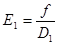
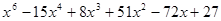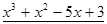
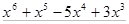
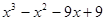
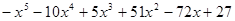
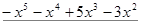
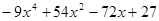
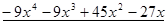
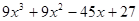
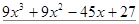
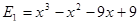
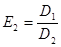
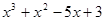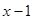
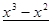
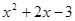
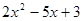
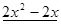
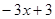
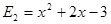
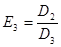
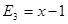
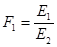
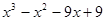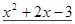
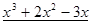
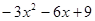
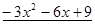
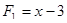
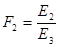
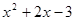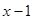
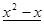
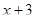
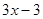
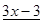
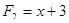
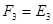
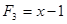
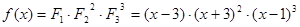
Многочлен 
имеет разложение в виде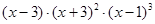 
.
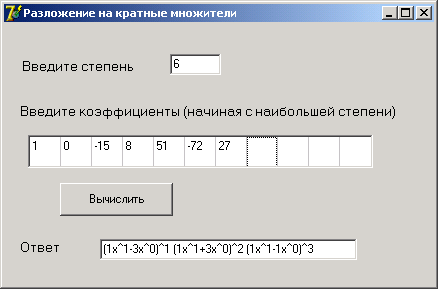
Я составила программу для разложения многочлена на кратные множители.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids;
type
TForm1 = class(TForm)
Edit1: TEdit;
Label1: TLabel;
SGd1: TStringGrid;
Label2: TLabel;
Button1: TButton;
Label3: TLabel;
SGd2: TStringGrid;
SGd3: TStringGrid;
SGd4: TStringGrid;
Edit6: TEdit;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
c,i,st1,st2,stiz,n_iz,n_nod,n,m,d_st,step,f:integer;
k,d,s:string;
kof1,kof2,k1,k2,izubst,a,b,a2,b2,buf,est,fxst:array[0..15] of integer;
izub,e,fx:array[0..50,0..50] of integer;
first:boolean;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var i,j,k_1,st3,l:integer;
sokr:boolean;
k2_2,k1_1:array[0..10] of integer;
begin
st1:=StrToInt(Edit1.Text);
for i:=0 to st1 do begin
SGd4.Cells[i,0]:=SGd1.Cells[i,0];
end;
repeat
n_iz:=n_iz+1;
st2:=st1-1;
for i:=0 to st1 do begin
if SGd1.Cells[i,0]<>'' then
kof1[st1-i]:=StrToInt(SGd1.Cells[i,0])
else MessageDlg('Внимание! Не введены значения коэффициентов!',mtWarning,[mbOK],0);
end;
s:='f(x)=';
for i:=st1 downto 0 do begin
if kof1[i]<>0 then begin
if(kof1[i-1]<0)or(i=0) then begin
str(kof1[i],d);
str(i,k);
s:=s+d+'x^'+k;
end
else begin
str(kof1[i],d);
str(i,k);
s:=s+d+'x^'+k+'+';
end;
end;
kof2[i-1]:=kof1[i]*i;
end;
//Edit2.Text:=s;
s:='f1(x)=';
for i:=st2 downto 0 do begin
SGd2.Cells[st2-i,0]:=inttostr(kof2[i]);
if kof2[i]<>0 then begin
if(kof2[i-1]<0)or(i=1) then begin
str(kof2[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(kof2[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
//Edit3.Text:=s;
end;
for i:=0 to st1 do begin
kof1[i]:=StrToInt(SGd1.Cells[i,0]);
k1[i]:=StrToInt(SGd1.Cells[i,0]);
|
|
|
end;
for i:=0 to st2 do begin
kof2[i]:=StrToInt(SGd2.Cells[i,0]);
k2[i]:=StrToInt(SGd2.Cells[i,0]);
end;
while kof2[0]<>0 do begin
repeat
//Edit4.Text:='';
stiz:=0;
k_1:=k1[0];
if k1[0]<>kof2[0] then begin
if (k1[0] mod kof2[0])=0 then begin
for j:=0 to st2 do
k2[j]:=(k1[0] div kof2[0])*kof2[j];
end
else begin
if k2[0]<>1 then
for j:=0 to st1 do
k1[j]:=kof2[0]*k1[j];
if k_1<>1 then begin
for j:=0 to st2 do
k2[j]:=k_1*kof2[j];
end;
end;
end;
for i:=1 to st1 do begin
k1[i-1]:=k1[i]-k2[i];
end;
st1:=st1-1;
until st1<st2;
if k1[0]<>0 then begin //Сокращение
sokr:=true;
for i:=1 to st1 do
if k1[i]<>0 then begin
if (k1[i] mod k1[0])<>0 then sokr:=false;
end;
k_1:=k1[0];
if sokr=true then
for i:=0 to st1 do
k1[i]:=k1[i] div k_1;
end;
for i:=0 to st2 do //Замена многочленов
k2_2[i]:=kof2[i];
for i:=0 to st1 do
k1_1[i]:=k1[i];
for i:=0 to 10 do begin
SGd3.Cells[i,0]:='';
SGd1.Cells[i,0]:='';
kof1[i]:=0;
k1[i]:=0;
kof2[i]:=0;
k2[i]:=0;
izub[n_iz,i]:=0;
end;
izubst[n_iz]:=st2;
for i:=0 to st2 do begin
k1[i]:=k2_2[i];
SGd1.Cells[i,0]:=inttostr(k1[i]);
izub[n_iz,i]:=k1[i];
if k1[i]<>0 then begin
//Edit4.Text:=Edit4.Text+IntToStr(k1[i])+'x^'+IntToStr(st2-i);
end;
if (k2_2[i+1]>0)and(i<st2) then //Edit4.Text:=Edit4.Text+'+';
end;
for i:=0 to st1 do begin
k2[i]:=k1_1[i];
kof2[i]:=k1_1[i];
end;
st3:=st1;
st1:=st2;
st2:=st3;
end;
until (st1=0);
d_st:=StrToInt(Edit1.Text);
for i:=d_st+1 downto 1 do begin
kof1[i]:=StrToInt(SGd4.Cells[d_st-(i-1),0]);
end;
//Нахождение Е
first:=true;
for n_nod:=1 to n_iz do begin
n:=d_st;
m:=izubst[n_nod];
d_st:=m;
for i:=n+1 downto 1 do begin
a[i]:=kof1[i];
end;
for i:=m+1 downto 1 do begin
b[i]:=izub[n_nod,m-(i-1)];
kof1[i]:=b[i];
end;
s:='f1(x)=';
for i:=n+1 downto 1 do begin
if a[i]<>0 then begin
if(a[i-1]<0)or(i=1) then begin
str(a[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(a[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
//Edit3.Text:=s;
s:='f2(x)=';
for i:=m+1 downto 1 do begin
if b[i]<>0 then begin
if(b[i-1]<0)or(i=1) then begin
str(b[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(b[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
//Edit4.Text:=s;
for j:=n+1 downto 1 do begin
a2[j]:=a[j];
b2[j]:=0;
end;
step:=n-m;
f:=n+2;
for i:=step+1 downto 1 do begin
f:=f-1;
buf[i]:=a2[f];
for j:=m+1 downto 1 do begin
b2[j]:=buf[i]*b[j];
end;
for j:=f downto 1 do begin
a2[j]:=a2[j]*b[m+1];
end;
for j:=f downto 1 do begin
a2[j]:=a2[j]-b2[j+1-i];
b2[j]:=0;
end;
end;
s:='h(x)=';
for i:=f+1 downto 1 do begin
e[n_nod,i]:=buf[i];
if buf[i]<>0 then begin
if(buf[i-1]<0)or(i=1) then begin
str(buf[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(buf[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
buf[i]:=0;
end;
end;
est[n_nod]:=f;
//Edit5.Text:=s;
s:='r(x)=';
for i:=n downto 0 do begin
if a2[i]<>0 then begin
if(a2[i-1]<0)or(i=1) then begin
str(a2[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(a2[i],d);
|
|
|
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
Edit6.Text:=s;
first:=false;
end;
for n_nod:=1 to n_iz-1 do begin
n:=est[n_nod];
m:=est[n_nod+1];
d_st:=m;
for i:=n+1 downto 1 do begin
a[i]:=e[n_nod,i];
end;
for i:=m+1 downto 1 do begin
b[i]:=e[n_nod+1,i];
kof1[i]:=b[i];
if n_nod=n_iz-1 then fx[n_iz,i]:=b[i];
end;
s:='f1(x)=';
for i:=n+1 downto 1 do begin
if a[i]<>0 then begin if(a[i-1]<0)or(i=1) then begin
str(a[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(a[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
//Edit3.Text:=s;
s:='f2(x)=';
for i:=m+1 downto 1 do begin
if b[i]<>0 then begin if(b[i-1]<0)or(i=1) then begin
str(b[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(b[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
//Edit4.Text:=s;
for j:=n+1 downto 1 do begin
a2[j]:=a[j];
b2[j]:=0;
end;
step:=n-m;
f:=n+2;
for i:=step+1 downto 1 do begin
f:=f-1;
buf[i]:=a2[f];
for j:=m+1 downto 1 do begin
b2[j]:=buf[i]*b[j];
end;
for j:=f downto 1 do begin
a2[j]:=a2[j]*b[m+1];
end;
for j:=f downto 1 do begin
a2[j]:=a2[j]-b2[j+1-i];
b2[j]:=0;
end;
end;
s:='h(x)=';
for i:=f+1 downto 1 do begin
fx[n_nod,i]:=buf[i];
if buf[i]<>0 then begin if(buf[i-1]<0)or(i=1) then begin
str(buf[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(buf[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
buf[i]:=0;
end;
end;
//Edit5.Text:=s;
fxst[n_nod]:=f;
s:='r(x)=';
for i:=n downto 0 do begin
if a2[i]<>0 then begin if(a2[i-1]<0)or(i=1) then begin
str(a2[i],d);
str(i-1,k);
s:=s+d+'x^'+k;
end
else begin
str(a2[i],d);
str(i-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
Edit6.Text:=s;
end;
fxst[n_iz]:=est[n_iz]+1;
Edit6.Text:='';
s:='';
for i:=1 to n_iz do begin
s:=s+'(';
for j:=fxst[i] downto 0 do begin
if fx[i,j]<>0 then begin
if(fx[i,j-1]<0)or(j=1) then begin
str(fx[i,j],d);
str(j-1,k);
s:=s+d+'x^'+k;
end
else begin
str(fx[i,j],d);
str(j-1,k);
s:=s+d+'x^'+k+'+';
end;
end;
end;
s:=s+')^'+IntToStr(i)+' ';
Edit6.Text:=Edit6.Text+s;
s:='';
end;
for i:=0 to 10 do begin
SGd1.Cells[i,0]:=SGd4.Cells[i,0];
end;
end;
end.
Заключение
При выполнении дипломной работы я рассмотрела следующие вопросы:
– делимость многочленов;
– деление многочленов с остатком;
– наибольший общий делитель, алгоритм Евклида;
– кратные корни;
– кратные множители, выделение кратных множителей;
– производные от многочленов.
Составила программы для нахождения частного и остатка при делении многочленов; наибольшего общего делителя двух многочленов; производной многочлена.
Список использованной литературы
1. Алгебра и теория чисел. Под ред. Н. Я. Виленкина. Москва: Просвещение, 1984.
2. Архангельский А. Я. Программирование в Delphi 6. Москва: ЗАО Бином, 2003.
|
|
|
3. Архангельский А. Я. Delphi 7. Справочное пособие. Москва: ООО Бином-Пресс, 2004.
4. Курош А. Г. Курс высшей алгебры. Москва: Наука, 1971.
5. Ляпин Е. С., Евсеев А. Е. Алгебра и теория чисел. Часть II. Линейная алгебра и полиномы. Москва: Просвещение, 1978.
6. Мантуров О. В. и др. Математика в понятиях, определениях и терминах. Часть 2. Москва: Просвещение, 1982.
7. Попов В.Б. Turbo Pascal. Москва: Финансы и статистика, 2000.
8. Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. Москва: Наука, 1980.
9. Сабинина Л. В. Математика в понятиях, определениях и терминах. Часть I. Москва: Просвещение, 1978.
10. Сборник задач по алгебре. Под ред. А. И. Кострикина. Москва: Наука, 1987.
11. Смолин Ю. Н. Алгебра и теория чисел. Перемь:1996.
12. Солодовников А. С., Родина М. А. Задачник-практикум по алгебре. Часть IV. Москва: Просвещение, 1985.
13. Фадеев Д. К. Лекции по алгебре. Москва: Наука, 1984.
14. Фадеев Д. К., Соминский И. С. Сборник задач по высшей алгебре. Москва: Наука, 1968.
15. Шварцбурд С. И. Избранные вопросы математики. Москва: Просвещение, 1980.
|
|
|
