 |
Наибольший общий делитель многочленов
|
|
|
|
Пусть даны произвольные многочлены 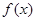 и
и  . Многочлен будет называться общим делителем для
. Многочлен будет называться общим делителем для 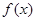 и
и  , если он служит делителем для каждого из этих многочленов. Свойство 5. показывает, что к числу общих делителей многочленов
, если он служит делителем для каждого из этих многочленов. Свойство 5. показывает, что к числу общих делителей многочленов 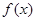 и
и  принадлежат все многочлены нулевой степени. Если других общих делителей эти два многочлена не имеют, то они называются взаимно простыми.
принадлежат все многочлены нулевой степени. Если других общих делителей эти два многочлена не имеют, то они называются взаимно простыми.
В общем же случае многочлены 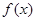 и
и  могут обладать делителями, зависящими от
могут обладать делителями, зависящими от  , и введем понятие о наибольшем общем делителе этих многочленов.
, и введем понятие о наибольшем общем делителе этих многочленов.
Наибольшим общим делителем отличных от нуля многочленов 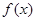 и
и  называется такой многочлен
называется такой многочлен  , который является их общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов. Обозначается наибольший общий делитель многочленов
, который является их общим делителем и, вместе с тем, сам делится на любой другой общий делитель этих многочленов. Обозначается наибольший общий делитель многочленов 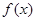 и
и  символом
символом 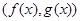 .
.
Это определение оставляет открытым вопрос, существует ли наибольший общий делитель для любых многочленов 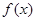 и
и  . Ответ на этот вопрос положительный. Существует метод для практического разыскания наибольшего общего делителя данных многочленов, называемый алгоритмом последовательного деления или алгоритмом Евклида.
. Ответ на этот вопрос положительный. Существует метод для практического разыскания наибольшего общего делителя данных многочленов, называемый алгоритмом последовательного деления или алгоритмом Евклида.
Алгоритм Евклида
Алгоритм Евклида – метод для нахождения наибольшего общего делителя двух целых чисел, а также двух многочленов от одного переменного. Он первоначально был изложен в «Началах» Евклида в геометрической форме как способ нахождения общей меры двух отрезков. Алгоритм Евклида для нахождения наибольшего общего делителя, как в кольце целых чисел, так и в кольце многочленов от одного переменного является частным случаем некого общего алгоритма в евклидовых кольцах.
Алгоритм Евклида для нахождения наибольшего общего делителя двух многочленов 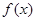 и
и  состоит в последовательном делении с остатком
состоит в последовательном делении с остатком 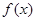 на
на  , затем
, затем  на первый остаток
на первый остаток  ,затем
,затем  на второй остаток
на второй остаток  и так далее. Так как степени остатков все время понижаются, то в этой цепочке последовательных делений мы дойдем до такого места, на котором деление совершится нацело и процесс остановится. Последний отличный от нуля остаток
и так далее. Так как степени остатков все время понижаются, то в этой цепочке последовательных делений мы дойдем до такого места, на котором деление совершится нацело и процесс остановится. Последний отличный от нуля остаток  , на который нацело делится предыдущий остаток
, на который нацело делится предыдущий остаток  , и является наибольшим общим делителем многочленов
, и является наибольшим общим делителем многочленов 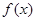 и
и  .
.
|
|
|
Для доказательства запишем изложенное в виде следующей цепочки равенств:

(2.4)

Последнее равенство показывает, что  служит делителем для
служит делителем для  . Отсюда следует, что оба слагаемых правой части предпоследнего равенства делятся на
. Отсюда следует, что оба слагаемых правой части предпоследнего равенства делятся на  , а поэтому
, а поэтому  будет делителем и для
будет делителем и для  . Далее, таким же путем, поднимаясь вверх, мы получим, что
. Далее, таким же путем, поднимаясь вверх, мы получим, что  является делителем и для
является делителем и для  , …,
, …,  ,
,  . Отсюда ввиду второго равенства, будет следовать, что
. Отсюда ввиду второго равенства, будет следовать, что  служит делителем для
служит делителем для  , а поэтому, на основании первого равенства, - и для
, а поэтому, на основании первого равенства, - и для  .
.
Возьмем теперь произвольный общий делитель  многочленов
многочленов  и
и  . Так как левая часть и первое слагаемое правой части первого из равенств делятся на
. Так как левая часть и первое слагаемое правой части первого из равенств делятся на  , то
, то  также будет делится на
также будет делится на  . Переходя ко второму и следующему равенствам, таким же способом получим, что на
. Переходя ко второму и следующему равенствам, таким же способом получим, что на  делятся многочлены
делятся многочлены  ,
,  , … Наконец, если уже будет доказано, что
, … Наконец, если уже будет доказано, что  и
и  делятся на
делятся на  , то из предпоследнего равенства получим, что
, то из предпоследнего равенства получим, что  делится на
делится на  . Таким образом,
. Таким образом,  на самом деле будет наибольшим общим делителем для
на самом деле будет наибольшим общим делителем для 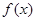 и
и  .
.
Мы доказали, что любые два многочлена обладают наибольшим общим делителем, и получили способ его вычисления. Этот способ показывает, что если многочлены 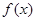 и
и  имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными, хотя у этих многочленов могут существовать и такие делители, не все коэффициенты которых рациональны (действительны).
имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными, хотя у этих многочленов могут существовать и такие делители, не все коэффициенты которых рациональны (действительны).
|
|
|
Если  есть наибольший общий делитель многочленов
есть наибольший общий делитель многочленов 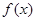 и
и  , то, как показывают свойства 8. и 9., в качестве наибольшего общего делителя этих многочленов можно было бы выбрать также многочлен
, то, как показывают свойства 8. и 9., в качестве наибольшего общего делителя этих многочленов можно было бы выбрать также многочлен  , где
, где  - произвольное число, отличное от нуля. Иными словами, их наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени. Ввиду этого можно условиться, что старший коэффициент наибольшего общего делителя двух многочленов будет всегда считаться равным единице. Используя это условие можно сказать, что два многочлена тогда и только тогда взаимно просты, если их наибольший общий делитель равен единице. В самом деле, в качестве наибольшего общего делителя двух взаимно простых многочленов можно взять любое число, отличное от нуля, но, умножая его на обратный элемент, получим единицу.
- произвольное число, отличное от нуля. Иными словами, их наибольший общий делитель двух многочленов определен лишь с точностью до множителя нулевой степени. Ввиду этого можно условиться, что старший коэффициент наибольшего общего делителя двух многочленов будет всегда считаться равным единице. Используя это условие можно сказать, что два многочлена тогда и только тогда взаимно просты, если их наибольший общий делитель равен единице. В самом деле, в качестве наибольшего общего делителя двух взаимно простых многочленов можно взять любое число, отличное от нуля, но, умножая его на обратный элемент, получим единицу.
Применяя алгоритм Евклида к многочленам с целыми коэффициентами, можем, чтобы избежать дробных коэффициентов, умножить делимое или сократить делитель на любое не равное нулю число, причем не только начиная какое-либо из последовательных делений, но и в процессе самого этого деления. Это будет приводить к искажению частного, но интересующие нас остатки будут приобретать лишь некоторый множитель нулевой степени, что при разыскании наибольшего общего делителя допускается.
Пример. Найти наибольший общий делитель многочленов  и
и  .
.
1.  и
и 
Совершим требуемые деления с остатком:
 |
| 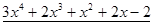








 |
| 








 |
| 




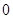
Построение последовательности Евклида закончено. Ее последний член 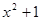 есть наибольший общий делитель исходных многочленов.
есть наибольший общий делитель исходных многочленов.
2.  и
и 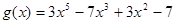
Совершим требуемые деления с остатком:
 │
│ 
 ||
|| 



 │
│ 





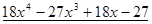

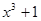
 │
│ 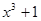





Построение последовательности Евклида закончено. Ее последний член 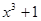 есть наибольший общий делитель исходных многочленов.
есть наибольший общий делитель исходных многочленов.
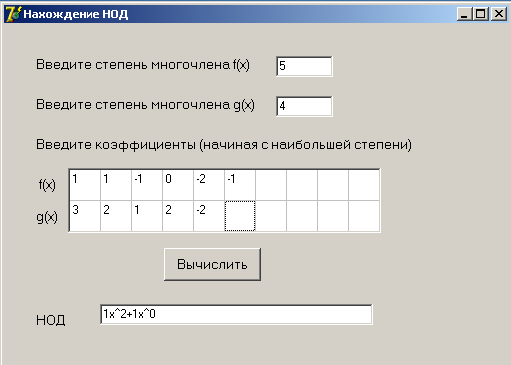
Я составила программу для нахождения наибольшего общего делителя двух многочленов:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Edit1: TEdit;
Edit2: TEdit;
SGd1: TStringGrid;
Label3: TLabel;
Button1: TButton;
Label4: TLabel;
Edit4: TEdit;
Label5: TLabel;
|
|
|
Label6: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
st1,st2:integer;
kof1,kof2,k1,k2:array[0..10] of integer;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var i,j,k_1,st3,l:integer;
sokr:boolean;
k2_2,k1_1:array[0..10] of integer;
begin
st1:=StrToInt(Edit1.Text);
st2:=StrToInt(Edit2.Text);
for i:=0 to st1 do begin
kof1[i]:=StrToInt(SGd1.Cells[i,0]);
k1[i]:=StrToInt(SGd1.Cells[i,0]);
end;
for i:=0 to st2 do begin
kof2[i]:=StrToInt(SGd1.Cells[i,1]);
k2[i]:=StrToInt(SGd1.Cells[i,1]);
end;
while kof2[0]<>0 do begin
repeat
Edit4.Text:='';
k_1:=k1[0];
if k1[0]<>kof2[0] then begin
if (k1[0] mod kof2[0])=0 then begin
for j:=0 to st2 do
k2[j]:=(k1[0] div kof2[0])*kof2[j];
end
else begin
if k2[0]<>1 then
for j:=0 to st1 do
k1[j]:=kof2[0]*k1[j];
if k_1<>1 then begin
for j:=0 to st2 do
k2[j]:=k_1*kof2[j];
end;
end;
end;
for i:=1 to st1 do begin
k1[i-1]:=k1[i]-k2[i];
end;
st1:=st1-1;
until st1<st2;
if k1[0]<>0 then begin //Сокращение
sokr:=true;
for i:=1 to st1 do
if k1[i]<>0 then begin
if (k1[i] mod k1[0])<>0 then sokr:=false;
end;
k_1:=k1[0];
if sokr=true then
for i:=0 to st1 do
k1[i]:=k1[i] div k_1;
end;
for i:=0 to st2 do //Замена многочленов
k2_2[i]:=kof2[i];
for i:=0 to st1 do
k1_1[i]:=k1[i];
for i:=0 to 10 do begin
kof1[i]:=0;
k1[i]:=0;
kof2[i]:=0;
k2[i]:=0;
end;
for i:=0 to st2 do begin
k1[i]:=k2_2[i];
if k1[i]<>0 then
Edit4.Text:=Edit4.Text+IntToStr(k1[i])+'x^'+IntToStr(st2-i);
if (k2_2[i+1]>0)and(i<st2) then Edit4.Text:=Edit4.Text+'+';
end;
for i:=0 to st1 do begin
k2[i]:=k1_1[i];
kof2[i]:=k1_1[i];
end;
st3:=st1;
st1:=st2;
st2:=st3;
end;
end;
end.
Используем алгоритм Евклида для доказательства следующей теоремы:
Теорема. Если  есть наибольший общий делитель многочленов
есть наибольший общий делитель многочленов  и
и  , то можно найти такие многочлены
, то можно найти такие многочлены  и
и  , что
, что
 . (2.5)
. (2.5)
Можно считать при этом, если степени многочленов  и
и  больше нуля, что степень
больше нуля, что степень  меньше степени
меньше степени  , а степень
, а степень  меньше степени
меньше степени  .
.
Доказательство основано на равенствах (2.4). Если учтем, что  , и положим
, и положим  ,
,  , то предпоследнее из равенств (2.4) даст:
, то предпоследнее из равенств (2.4) даст:

 .
.
Подставляя сюда выражение  через
через  и
и  из предшествующего равенства (2.4), получим:
из предшествующего равенства (2.4), получим:
 ,
,
где  ,
,  . Продолжая подниматься вверх по равенствам (2.4), придем к доказываемому равенству (2.5).
. Продолжая подниматься вверх по равенствам (2.4), придем к доказываемому равенству (2.5).
Для доказательства второго утверждения теоремы предположим, что многочлены  и
и  , удовлетворяющие равенству (2.5), уже найдены, но, например, степень
, удовлетворяющие равенству (2.5), уже найдены, но, например, степень  больше или равна степени
больше или равна степени  . Делим
. Делим  на
на  :
:
|
|
|
 ,
,
где степень  меньше степени
меньше степени  , и подставляем это выражение в (2). Получим равенство:
, и подставляем это выражение в (2). Получим равенство:

 .
.
Степень множителя, стоящего при  , уже меньше степени
, уже меньше степени  . Степень многочлена, стоящего в квадратных скобках, будет в свою очередь меньше степени
. Степень многочлена, стоящего в квадратных скобках, будет в свою очередь меньше степени  , так как в противном случае степень второго слагаемого левой части была бы не меньше степени
, так как в противном случае степень второго слагаемого левой части была бы не меньше степени  , а так как степень первого слагаемого меньше степени этого произведения, то вся левая часть имела бы степень, большую или равную степени
, а так как степень первого слагаемого меньше степени этого произведения, то вся левая часть имела бы степень, большую или равную степени  , тогда как многочлен
, тогда как многочлен  заведомо имеет, при наших предположениях, меньшую степень.
заведомо имеет, при наших предположениях, меньшую степень.
Теорема доказана.
Одновременно получаем, что если многочлены  и
и  имеют рациональные или действительные коэффициенты, то и многочлены
имеют рациональные или действительные коэффициенты, то и многочлены  и
и  , удовлетворяющие равенству (2.5), можно подобрать так, что их коэффициенты будут рациональными или, соответственно действительными.
, удовлетворяющие равенству (2.5), можно подобрать так, что их коэффициенты будут рациональными или, соответственно действительными.
Применяя доказанную теорему к взаимно простым многочленам, получаем такой результат:
Многочлены  и
и  тогда и только тогда взаимно просты, если можно найти многочлены
тогда и только тогда взаимно просты, если можно найти многочлены  и
и  , удовлетворяющие равенству
, удовлетворяющие равенству
 . (2.6)
. (2.6)
Опираясь на этот результат, можно доказать несколько простых, но важных теорем о взаимно простых многочленах:
Теорема 1. Если многочлен  взаимно прост с каждым из многочленов
взаимно прост с каждым из многочленов  и
и  , то он взаимно прост и с их произведением.
, то он взаимно прост и с их произведением.
Доказательство. В самом деле, существуют, по (2.6), такие многочлены  и
и  , что
, что  .
.
Умножая это равенство на  , получаем:
, получаем:
 ,
,
откуда следует, что всякий общий делитель  и
и  был бы делителем и для
был бы делителем и для  ; однако по условию
; однако по условию  .
.
Теорема 2. Если произведениемногочленов  и
и  делится на
делится на  , но
, но  и
и  взаимно просты, то
взаимно просты, то  делится на
делится на  .
.
Доказательство. Умножая равенство  на
на  , получим:
, получим:  .
.
Оба слагаемых левой части этого равенства делятся на  ; на него делится, следовательно, и
; на него делится, следовательно, и  .
.
Теорема 3. Если многочлен  делится на каждый из многочленов
делится на каждый из многочленов  и
и  , которые между собой взаимно просты, то
, которые между собой взаимно просты, то  делится и на их произведение.
делится и на их произведение.
Доказательство. Действительно,  , так что произведение, стоящее справа, делится на
, так что произведение, стоящее справа, делится на 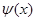 . Поэтому, по теореме 2,
. Поэтому, по теореме 2,  делится на
делится на 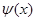 ,
,  , откуда
, откуда  .
.
Определение наибольшего общего делителя может быть распространен на случай любой конечной системы многочленов: наибольшим общим делителем многочленов  называется такой общий делитель этих многочленов, который делится на любой другой общий делитель этих многочленов. Существование наибольшего общего делителя для любой конечной системы многочленов вытекает из следующей теоремы, дающей также способ его вычисления.
называется такой общий делитель этих многочленов, который делится на любой другой общий делитель этих многочленов. Существование наибольшего общего делителя для любой конечной системы многочленов вытекает из следующей теоремы, дающей также способ его вычисления.
Теорема. Наибольший общий делитель многочленов  равен наибольшему общему делителю многочлена
равен наибольшему общему делителю многочлена  и наибольшего общего делителя многочленов
и наибольшего общего делителя многочленов 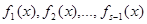 .
.
|
|
|
Доказательство. В самом деле, при 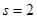 теорема очевидна. Примем поэтому, что для случая
теорема очевидна. Примем поэтому, что для случая  она справедлива, то есть, в частности, уже доказано существование наибольшего общего делителя
она справедлива, то есть, в частности, уже доказано существование наибольшего общего делителя  многочленов
многочленов  . Обозначим через
. Обозначим через  наибольший общий делитель многочленов
наибольший общий делитель многочленов  и
и  . Он будет общим делителем для всех заданных многочленов. С другой стороны, всякий другой общий делитель этих многочленов будет делителем также и для
. Он будет общим делителем для всех заданных многочленов. С другой стороны, всякий другой общий делитель этих многочленов будет делителем также и для  , а поэтому и для
, а поэтому и для  .
.
В частности, система многочленов  называется взаимно простой, если общими делителями этих многочленов являются лишь многочлены нулевой степени, то есть если их наибольший общий делитель равен 1. Если
называется взаимно простой, если общими делителями этих многочленов являются лишь многочлены нулевой степени, то есть если их наибольший общий делитель равен 1. Если  , то попарно эти многочлены могут и не быть взаимно простыми.
, то попарно эти многочлены могут и не быть взаимно простыми.
Кратные корни
Теорема Безу. Многочлен f (x) делится на x - c тогда и только тогда, когда число c является его корнем.
Рассмотрим произвольный многочлен f (x) и разделим его с остатком на двучлен x - c. Поскольку степень этого двучлена равна 1, то остаток либо равен 0, либо имеет степень 0. И в том, и в другом случае остаток r есть число. Таким образом, многочлен f (x) представляется в виде:
f (x)= (x - c) q (x)+ r.
Положив в этом тождестве x = c, получим что f (c)= r. Мы доказали тем самым, что остаток от деления многочлена на двучлен x - c равен значению многочлена при x = c.
С помощью теоремы Безу решим несколько задач.
Пример 1. Решить уравнение 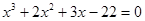 .
.
Многочлен f (x)=  имеет корень 2. По теореме Безу f (x) делится на x -2, то есть имеет место равенство
имеет корень 2. По теореме Безу f (x) делится на x -2, то есть имеет место равенство
 .
.
 |
| 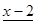







Остается решить квадратное уравнение  .
.
Это уравнение не имеет действительных корней, так что x =2 – единственный действительный корень исходного уравнения.
2. Решить уравнение  .
.
Многочлен f (x)=  имеет корень -2. По теореме Безу f (x) делится на x +2, то есть имеет место равенство
имеет корень -2. По теореме Безу f (x) делится на x +2, то есть имеет место равенство  .
.
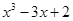 |
| 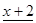





0
Остается решить квадратное уравнение  .
.
Это уравнение имеет корень 1. Так что x =-2 и x =1 – корни исходного уравнения.
Если c – корень многочлена f (x), то есть f (c)=0, то f (x) делится на x - c. Может оказаться, что многочлен f (x) делится не только на первую степень линейного двучлена x - c, но и на более высокие его степени. Во всяком случае, найдется такое натуральное число k, что f (x) нацело делится на  , но не делится на
, но не делится на  . Поэтому
. Поэтому
 ,
,
где многочлен  на x - c уже не делится, то есть число с своим корнем не имеет. Число k называется кратностью корня c в многочлене f (x), а сам корень c – k - кратным корнем этого многочлена. Если k =1, то говорят, что корень с – простой.
на x - c уже не делится, то есть число с своим корнем не имеет. Число k называется кратностью корня c в многочлене f (x), а сам корень c – k - кратным корнем этого многочлена. Если k =1, то говорят, что корень с – простой.
Производная от многочлена
Понятие кратного корня тесно связано с понятием производной от многочлена. Мы изучаем многочлены с любыми комплексными коэффициентами и поэтому не можем просто воспользоваться понятием производной, введенным в курсе математического анализа. То, что будет сказано ниже, следует рассматривать как независимое от курса анализа определение производной многочлена.
Пусть дан многочлен n–ной степени
f (x)= 
с любыми комплексными коэффициентами. Его производной (первой производной) называется многочлен (n- 1)-й степени

Производная от многочлена нулевой степени и от нуля считается равной нулю. Производная от первой производной называется второй производной от многочлена f (x) и обозначается через f “(x). Очевидно, что

и по этому  , то есть (n+1)-я производная от многочлена n–й степени равна нулю.
, то есть (n+1)-я производная от многочлена n–й степени равна нулю.
Свойства, являющиеся формулами дифференцирования для суммы и произведения:
1.  (4.1)
(4.1)
2.  (4.2)
(4.2)
Эти формулы легко проверить, впрочем, непосредственным подсчетом, беря в качестве и два произвольных многочлена и применяя данное выше определение производной.
Формула (4.2) распространяется на случай произведения любого конечногочисла множителей, а поэтому выводится формула для производной от степени:
3.  (4.3)
(4.3)
Доказательство. Используем метод математической индукции.






 .
.
Если число с является k –кратным корнем многочлена f (x), то при k >1 оно будет (k -1)–кратным корнем первой производной этого многочлена; если же k =1, то с не будет служить корнем для  .
.
В самом деле, пусть
 ,
,  , (4.4)
, (4.4)
где  уже не делится на х-с. Дифференцируя равенство (4.4), получаем:
уже не делится на х-с. Дифференцируя равенство (4.4), получаем:
 .
.
Первое слагаемое суммы делится на х-с, а второе на х-с не делится; поэтому вся эта сумма на х-с не может делиться. Учитывая, что частное от деления f (x) на 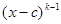 определено однозначно, мы получаем, что
определено однозначно, мы получаем, что  является наибольшей степенью двучлена х-с, на которую делится многочлен
является наибольшей степенью двучлена х-с, на которую делится многочлен  .
.
Применяя эту теорему несколько раз, мы получаем, что k -кратный корень многочлена f (x) будет (k - s)-кратным в s -й производной этого многочлена  и впервые не будет служить корнем для k -й производной от f (x).
и впервые не будет служить корнем для k -й производной от f (x).
Пример. Найти производную  многочлена
многочлена  .
.

 .
.
Я составила программу для нахождения первой производной многочлена.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids;
type
TForm1 = class(TForm)
Edit1: TEdit;
Label1: TLabel;
SGd1: TStringGrid;
Label2: TLabel;
Button1: TButton;
Edit2: TEdit;
Edit3: TEdit;
Label3: TLabel;
Label4: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
c,i,st:integer;
k,l,s:string;
kof:array[0..100] of integer;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
begin
st:=StrToInt(Edit1.Text);
for i:=0 to st do begin
if SGd1.Cells[i,0]<>'' then
kof[st-i]:=StrToInt(SGd1.Cells[i,0])
else MessageDlg ('Внимание! Не введены значения коэффициентов!',mtWarning,[mbOK],0);
end;
s:='f(x)=';
for i:=st downto 0 do begin
if kof[i]<>0 then begin
if(kof[i-1]<0)or(i=0) then begin
str(kof[i],l);
str(i,k);
s:=s+l+'x^'+k;
end
else begin
str(kof[i],l);
str(i,k);
s:=s+l+'x^'+k+'+';
end;
end;
kof[i]:=kof[i]*i;
end;
Edit2.Text:=s;
s:='f1(x)=';
for i:=st downto 0 do begin
if kof[i]<>0 then begin
if(kof[i-1]<0)or(i=1) then begin
str(kof[i],l);
str(i-1,k);
s:=s+l+'x^'+k;
end
else begin
str(kof[i],l);
str(i-1,k);
s:=s+l+'x^'+k+'+';
end;
end;
Edit3.Text:=s;
end;
end;
end.

Кратные множители
Существуют методы, позволяющие узнать, обладает ли данный многочлен кратными множителями, и в случае положительного ответа дающие возможность свести изучение этого многочлена к изучению многочленов, уже не содержащих кратных множителей.
Теорема. Если  является
является  - кратным неприводимым множителем многочлена
- кратным неприводимым множителем многочлена  ,
,  , то он будет
, то он будет  - кратным множителем производной этого многочлена. В частности, простой множитель многочлена. Не входит в разложение производной.
- кратным множителем производной этого многочлена. В частности, простой множитель многочлена. Не входит в разложение производной.
В самом деле, пусть
 , (5.1)
, (5.1)
причем  уже не делится на
уже не делится на 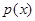 . Дифференцируя равенство (5.1), получаем:
. Дифференцируя равенство (5.1), получаем:
 .
.
Второе из слагаемых, стоящих в скобках, не делится на  . Действительно,
. Действительно,  не делится
не делится 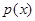 по условию,
по условию,  имеет меньшую степень, т.е. также не делится на
имеет меньшую степень, т.е. также не делится на  . С другой стороны, первое слагаемое суммы, стоящей в квадратных скобках, делиться на
. С другой стороны, первое слагаемое суммы, стоящей в квадратных скобках, делиться на  , т.е. множитель
, т.е. множитель  , на самом деле входит в
, на самом деле входит в  с кратностью
с кратностью  .
.
Из данной теоремы и из указанного выше способа разыскания наибольшего общего делителя двух многочленов следует, что если дано разложение многочлена  на неприводимые множители:
на неприводимые множители:
 , (5.2)
, (5.2)
то наибольший общий делитель многочлена  и его производной обладает следующим разложением на неприводимые множители:
и его производной обладает следующим разложением на неприводимые множители:
 , (5.3)
, (5.3)
где множитель  следует при
следует при  заменять единицей. В частности, многочлен
заменять единицей. В частности, многочлен  тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.
тогда и только тогда не содержит кратных множителей, если он взаимно прост со своей производной.
|
|
|


