Фундаментальное свойство энтропии дискретных эргодических процессов

Мы рассмотрели неопределенность и ее меру – энтропию – для случайных величин и событий. Необходимо теперь сделать следующий шаг – обобщить эти понятия таким образом, чтобы иметь возможность оценивать неопределенность случайных процессов.

Случайный процесс X_t можно рассматривать как множество случайных величин, определенных на множестве значений параметра t (для конкретности считаем, что t является временем). Исходя из этого, неопределенность случайного процесса можно определить как неопределенность всей совокупности случайных величин, образующих процесс X_t. Следует при этом отметить ряд особенностей такого представления.

Во-первых, нецелесообразно оценивать неопределенность случайного процесса на всей оси времени, от -¥ до +¥, так как в общем случае это сразу же приведет к бесконечным величинам. Естественно, возникает вопрос о возможности введения меры средней неопределенности случайного процесса, приходящейся на некоторый интервал времени, в частности – на единичный интервал.

Во-вторых, при вычислении энтропии множества реализаций случайного процесса конечной длины возникаетнеобходимость учета статистической связи между случайными величинами, соответствующими различным значениям параметра t.

Имея в виду эти и другие особенности энтропийного описания непрерывных процессов, обратимся сначала к рассмотрению простого случая – стационарного процесса с дискретным временем и дискретным конечным множеством возможных состояний в каждый момент времени.

Рассмотрим множество реализаций такого случайного процесса длительностью в п элементов. Если множество возможных состояний каждого элемента насчитывает т состояний, то общее число отличающихся между собой реализаций будет равно т^п. Осуществление каждой реализации можно рассматривать как осуществление случайного события из т^п возможных событий. Зная распределение вероятностей возможных состояний каждого элемента и характер связей между элементами, можно вычислить вероятность каждой из т^п реализаций, р(С). Теперь, в полном соответствии с тем, как это делалось для обычных случайных событий, мы можем вычислить энтропию множества п- членных реализаций:

(5.10)

Величина H_n, конечно, зависит от того, каково п. Желая образовать унифицированную энтропийную характеристику случайного процесса, естественно ввести в рассмотрение величину

(5.11)

если, конечно, указанный предел существует. Величина H будет характеризовать среднюю неопределенность, приходящуюся на один элемент процесса, и может быть названа энтропией процесса.

В [7] доказывается, что для каждого стационарного процесса предел (5.11) действительно существует.

Для каждого из т ^п событий можно определить его вероятность р(С). На множестве этих событий можно задать любую числовую функцию f_n(C), которая будет, очевидно, случайной величиной. В частности, такой случайной величиной будет числовая функция:

Математическое ожидание этой функции находится обычным образом:

(5.12)

Отсюда сразу следует, что

(5.13)

Поскольку предел 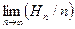существует, то и

(5.14)

т.е. при п ® ¥ математическое ожидание случайной величины имеет пределом энтропию случайного процесса Н [7].

Это соотношение между Н и Р(С) является одним из проявлений общего свойства дискретных эргодических процессов. Оказывается, что не только математическое ожидание величины f_n(C) при п ® ¥ имеет пределом Н, но и сама эта величина f_n(C) стремится по вероятности к Н при п ® ¥. Другими словами, как бы малы ни были e > 0и d > 0, при достаточно большом п вероятность неравенства > e будет меньше, чем d; близость f_n(C) к Н при больших п является почти достоверным событием.

Это фундаментальное свойство эргодических процессов впервые было обнаружено К. Шенноном [4] на примерах процесса с независимыми элементами и простой марковской цепи. Позднее было доказано, что этим свойством обладают любые эргодические процессы [7].