Статистическая мера количества информации

Меру количества информации, получаемой в результате того или иного опыта, можно было бы установить как функцию отношения числа равновозможных ответов до опыта (п)и после опыта (п_с),т. е. как функцию отношения . Интуиция подсказывает, что количество получаемой в результате опыта информации должно быть тем больше, чем больше это отно­шение. Вместо понятия «равновозможные события» (или ответы) удобнее пользоваться понятием о «вероятности этих событий».

Если рассматриваемые события (ответы) равновозможны, то априорная (доопытная) вероятность события х_i равна, очевидно, , а апостериорная (после опыта или после сообщения) вероятность . В таком случае количество информации, которое мы получаем о событии x_i в результате опыта, должно быть функцией отношения

.

 

Наиболее удобной является логариф­мическая функция, и, следовательно, количество информации, полу­чаемое о событии x_i в результате опыта, может быть принято равным

.

 

Выбор коэффициента K и основания логарифмов (а)не имеет прин­ципиального значения, ибо он определяет лишь масштаб или единицу количества информации. Обычно выбирают логарифм с основанием два (а = = 2) и K = 1, тогда

дв. ед. (5.22)

 

Единица количества информации при таком выборе а и K называется двоичной.

Получение одной двоичной единицы количества информации соответствует тому, что мы узнаем, какое из двух равновозможных событий имеет место или какая из двух равновозможных гипотез правильна. Такими двумя событиями (гипотезами) могут быть также ответы «да» или «нет» на какой-либо вопрос. Если эти ответы равновозможны (равновероятны), то, получив один из них, мы тем самым получаем одну двоичную единицу информации.

Если события (ответы) равновозможны и если к тому же p_c (i) =1, т.е. после опыта ситуация полностью определена, формула (6.1) может быть представлена в виде

. (5.23)

 

Определим количественную меру информации при конечном ансамбле независимых событий. Формула (5.22) устанавливает непосред­ственную связь между количеством информации, получаемой о неко­тором событии в результате опыта, и изменением вероятности этого события до и после опыта. Эта связь может быть обобщена и на случай, когда имеется некоторое конечное множество независимых событий с разными априорными вероятностями.

Рассмотрим некоторое конечное множество X событий x ₁, x ₂, …, x_n. Допустим, что данные события независимы и несовместны, а априорные вероятности их соответственно равны р (х ₁), р (x ₂), …, р (х_п),причем р (х ₁)+ + р (x ₂)+ … + р (х_п) = 1. Последнее означает, что в течение некоторого наблюдаемого отрезка времени всегда происходит одно из этих событий.

Рассматриваемый ансамбль событий может быть описан конечной схемой вида

. (5.24)

Ансамбль рассматривается как некоторая модель физической системы, которая может находиться в п различных состояниях или в которой может происходить п различных событий. Рассматри­вается случай, когда эти состояния или события независимы и не­совместны.

Используя формулу (5.22), можно сказать, что достоверное сообщение о том, что из всех событий х происходит событие x_i, несет в себе количество информации, равное

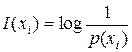дв. ед. (5.25)

 

Следовательно, сообщение о событии несет тем большее количество информации, чем меньше априорная вероятность этого события. Это положение хорошо согласуется с интуитивным представлением об информации. Так, например, сообщение о том, что летом дни длиннее ночи, для любого человека с минимальным жизненным опытом или образованием не несет никакой информации, ибо этот факт априори (до этого сообщения) уже ему известен.

Формула (5.25) указывает, что в конечном ансамбле X сообщения о разных событиях в общем случае несут разное количество инфор­мации. При решении большинства задач, связанных с построением систем передачи и преобразования информации, необходимо знать среднее количество информации, приходящееся на одно сообщение. Последнее в соответствии с правилами теории вероятности может быть определено как математическое ожидание величины I (x_i),т. е.

 

и, следовательно,

дв.ед./сообщ. (5.26)

 

В данном случае через I (X) обозначено среднее количество информации, приходящееся на одно достоверное сообщение о событии х при передаче большого числа таких сообщений. Это соотношение носит название формулы Шеннона.

Количество информации, определяемое формулой (5.26), принято называть полным или средним количеством информации ансамбля событий { Х }, а каждое слагаемое –log p (x _i) – частным количеством информации, получаемым от отдельного i -го события, состоящего в том, что ансамбль { Х } находится в состоянии x_i.

Обращает на себя внимание тот факт, что формула Шеннона (5.26) для количества информации совпадает с формулой для величины энтропии множества возможных сигналов. Это совпадение не является случайным и ниже будет рассмотрено более детально. Здесь же пока констатируем этот важный факт: при отсутствии ошибок при приеме среднее количество информации на сигнал численно равно энтропии множества возможных сигналов. Из этого, однако, не следует, что энтропия и количество информации это одно и то же.

Снимем теперь условие статистической независимости между символами, которое накладывалось на сигнал при построении количественной меры информации по Хартли. По-прежнему пока остается в силе условие отсутствия ошибок.

Рассмотрим важный случай такой статистической зависимости, которая имеет место между элементами простой цепи Маркова.

Очевидно, что энтропия символа, который должен осуществиться, теперь зависит от того, какой символ осуществился только что перед ним. Пусть, например, последним символом был символ под номером i. Тогда энтропия следующего символа (при условии, что предыдущий известен) равна

(5.27)

где 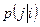- вероятность того, что после символа i осуществится символ j. Нас, однако, интересует безусловная энтропия Н символа в цепи Маркова, т.е. средняя величина . ПО определению среднего,

(5.28)

Эти соотношения и дают нам искомый результат.

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: