Количество информации как мера снятой неопределенности

В статистической теории информации рассматриваются ансамбли или системы событий, которым присуща некоторая неопределенность.

В результате получения некоторого сообщения, представляющего собой результат выбора из ансамбля событий, априорная неопределенность может быть уменьшена. Так как степень неопределенности измеряется величиной энтропии, то в качестве меры количества информацииоб ансамбле событий естественно принять изменение (уменьшение) энтропии ансамбля в результате получения сообщения. То есть при статистическом подходе энтропия есть мера недостатка информации об ансамбле событий, а количество информации представляет собой разность априорной и апостериорной энтропий ансамбля событий.

Если в результате сообщения состояние ансамбля или системы событий стало известным (апостериорная энтропия ансамбля стала равной нулю), то количество информации, содержащееся в ансамбле событий, равно его априорной энтропии

 

I (Х) = H (Х) – 0 = 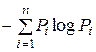,(5.29)

 

где I (Х) – количество информации ансамбля событий { Х }; H (Х) – априорная энтропия ансамбля { Х }.

Таким образом, в результате приема сигнала, с одной стороны, произошло уменьшение неопределенности с H (x) до нуля, а с другой стороны – получено количество информации I, численно равное Н.

Обычно на практике информацию об исследуемом ансамбле{ Х } приходится определять не непосредственно, а по состоянию некоторого ансамбля или системы { Y }, связанного с { X }. В общем случае ансамбли { X } и { Y } отличаются друг от друга и различие состоит в следующем.

Во-первых, ансамбли { X } и { Y } могут различаться за счет того, что некоторые события { x_i } интересующего нас ансамбля { X } не отражены в совокупности { y_i } событий ансамбля { Y } и наоборот.

Во-вторых, различия могут возникнуть за счет погрешностей определения (например, измерения) состояния ансамбля { X } или ошибок при передаче сообщения об ансамбле { X }.

В связи с этим найдем, какое количество информации об ансамбле { X } дает установление состояния ансамбля { Y }.

Определим это количество информации как уменьшение энтропии ансамбля { X } в результате получения сообщения об ансамбле { Y }, с ним связанного

I (X, Y) = H (X) - H (X ç Y), (5.30)

 

где H (X) – априорная энтропия ансамбля { X }; H (X ô Y) – энтропия ансамбля { X }, оставшаяся после получения сообщения об ансамбле { Y }.

Выражение (5.30) называется полным количеством информации об ансамбле { X }, содержащимся в ансамбле { Y }. Можно показать, что количество информации, содержащееся в ансамбле { Y } относительно { X }, такое же, как и в ансамбле { X } относительно { Y }

 

I (X, Y) = I (Y, X) = H (X) – H (X ô Y) = H (Y) – H (Y ô X). (5.31)

Количество информации, определяемое формулами (5.30) и (5.31) как разность априорной и апостериорной энтропий ансамбля событий, называется количеством полной взаимной информации, содержащейся в ансамблях { X }и { Y }.

Итак, количество информации определяем как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропии этого объекта.

В явной форме равенство (5.30) запишется так:

 

I (X, Y) = H (X)– H (X | Y)=

(5.32)

 

а для равенства (5.31) имеем

 

(5.33)

 

Этим формулам легко придать полную симметричность: умножив и разделив логарифмируемое выражение в (5.32) на р (у_k), а в (5.33) на p (x_i), сразу получим, что

 

(5.34)

 

Эту симметрию можно интерпретировать так: количество информации в объекте X об объекте Y равно количеству информации в объекте Y об объекте X. Таким образом, количество информации является не характеристикой одного из объектов, а характеристикой их связи, соот­ветствия между их состояниями. Подчеркивая это, можно сформулировать еще одно определение: среднее количество информации, вычисляемое по формуле (5.34), есть мера соответствия двух случайных объектов.

Это определение позволяет прояснить связь понятий информации и количества информации. Информация есть отражение одного объекта другим, проявляющееся в соответствии их состояний. Один объект может быть отражен с помощью нескольких других, часто какими-то лучше, чем остальными. Среднее количество информации и есть числовая характеристика степени отражения, степени соответствия. Под­черкнем, что при таком описании как отражаемый, так и отражающий объекты выступают совершенно равноправно. С одной стороны, это подчеркивает обоюдность отражения: каждый из них содержит информацию друг о друге. Это представляется естественным, поскольку отра­жение есть результат взаимодействия, т.е. взаимного, обоюдного изме­нения состояний. С другой стороны, фактически одно явление (или объект) всегда выступает как причина, другой – как следствие; это никак не учитывается при введенном количественном описании информации.

Для однозначного определения единицы измерения энтропии необходимо конкретизировать число m состояний объекта и основание логарифма. Возьмем для определенности наименьшее число возможных состояний, при котором объект еще остается случайным, т.е. m = 2, и в качестве основания логарифма также возьмем число 2. Тогда из равенства –p ₁log₂ p ₁– p ₂log₂ р ₂= 1 вытекает, что р, p ₁ = р ₂= 1/2. Сле­довательно, единицей неопределенности служит энтропия объекта с дву­мя равновероятными состояниями. Эта единица получила название «бит». Бросание монеты дает количество информации в один бит. Дру­гая единица («нит») получается, если использовать натуральные лога­рифмы, обычно она употребляется для непрерывных величин.

Следует отметить, что введенная количественная ме­ра информации совершенно не учитывает полезность, ценность или важность сообщений. Так, сообщение об оценке, полученной в школе учеником, неопределенность априорной информации о которой может быть достаточ­но большой, при использовании этой меры может содер­жать большее количество информации, чем сообщение о состоянии здоровья ребенка. Именно абстрагирование от качественных характеристик сообщения позволила создать строгий и изящный математический аппарат для характеристики информации. Однако в некоторых областях применения (в частности, в теории массового об­служивания), где учет полезности и важности информации существен, эта особенность меры информации, введенной Шенноном, создает определенные затруднения в использовании аппарата теории информации. Этот не­достаток обычно исправляют разделением сообщений на категории с введением соответствующих приоритетов или весовых коэффициентов.

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: