Циклические полиены (аннулены).

Метод МО Хюккеля

Метод молекулярных орбиталей Хюккеля (МОХ) является одним из наиболее простых и полезных вариантов общего метода МО ЛКАО. В его основе лежит несколько приближений, позволяющих избежать вычислительных трудностей, характерных для полного варианта метода МО.

Каждая МО в методе Хюккеля строится в виде линейной комбинации атомных орбиталей (ЛКАО):

y _i = С ₁ × j ₁ + С ₂ × j ₂ +... + С_n × j _n

где n — число атомов. Полный набор МО удобно задать в матричном виде:

Система уравнений Рутана для нахождения коэффициентов С_{i m} имеет вид:

где F_ij — матричные элементы оператора Фока, S_ij — интегралы перекрывания для данной пары атомов, e — орбитальная энергия.

Основные проблемы метода МО, как известно, связаны с необходимостью процедуры самосогласования, включающей многократные вычисления интегралов типа F и S. В методе Хюккеля ни один из этих интегралов не вычисляется — они определяются на основании экспериментальных данных (спектральные, калориметрические и т.д.). Таким образом МОХ относится к большой группе т.н. полуэмпирических вариантов общего метода МО.

Еще одно приближение метода Хюккеля заключается в том, что все диагональные интегралы F_ii (оба индекса одинаковы), характеризующие некоторый атом (точнее, энергию электрона, локализованного на этом атоме), полагаются равными друг другу и поэтому обозначаются одним и тем же символом: F_ii = F_jj = a (т.н. остовный интеграл). Другими словами, предполагается, что все атомы, входящие в состав молекулы, одинаковы по своей химической природе. Поэтому простой метод МОХ применяется почти исключительно для описания углеводородов типа полиенов и аренов. Существуют и усовершенствованные разновидности метода МОХ, позволяющие учесть различия в природе атомов гетероатомных молекул.

Третье приближение сводится к тому, что недиагональные интегралы F_ij разделяются на два типа. Первый тип относится к парам атомов, соединенными между собой химическими связями. Для таких пар атомов принимается следующее условие: F_ij = b (т.н. резонансный интеграл). Второй тип относится к парам атомов, которые не связаны между собой химически; для них F_ij = 0.

Резонансный интеграл представляет собой поправку к полной энергии, обусловленную возможностью перехода электрона от атома j к атому i, и наоборот. Химически связанные атомы располагаются близко друг к другу и амплитуда обмена электронами для такой пары атомов велика. Напротив, химически несвязанные атомы практически не могут обмениваться электронами, и, следовательно, соответствующая поправка к энергии настолько мала, что ею можно пренебречь. Заметим, что разделение недиагональных интегралов F_ij на два типа (нулевые и ненулевые) осуществляется не на основании квантовомеханических соображений, а исключительно на химической основе — по химической структурной формуле. Структура матрицы уравнений Рутана в методе Хюккеля определенным образом "приспосабливается" к топологии молекулы. Поэтому метод МОХ относится к классу т.н. топологических вариантов МО.

Четвертое приближение заключается в том, что интегралы перекрывания S_ij также разделяются на два типа: диагональные интегралы приравниваются к 1, а недиагональные к 0:

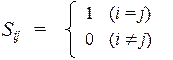
Такой подход называется приближением нулевого дифференциального перекрывания (НДП).

После сделанных приближений, матрица уравнения Рутана существенно упрощается — она уже не содержит интегралов (типа F _mnи S _mn), которые надо вычислять итерационным методом ССП, а содержит только небольшое число констант a и b, значения которых предполагаются заранее известными, а также параметр e. Поэтому интегро-дифференциальная система уравнений Рутана превращается в методе МОХ в обычную систему линейных уравнений, которую можно легко решить стандартными методами линейной алгебры.

Эта система имеет следующий вид: по диагонали матрицы стоят числа (a – e), а недиагональные элементы равны либо числу b, либо или нулю, в зависимости от топологии молекулы. С целью упрощения, можно провести дополнительное преобразование: разделим все элементы матрицы на число b. Т огда диагональные элементы приобретают вид (a – e)/ b = х, а недиагональные элементы будут равны или 0/ b = 0, или b / b = 1:

Заметим, что эта система является однородной (все правые части равны 0). Такие системы имеют решения только тогда, когда определитель системы равен нулю.

Раскрыв этот определитель, получим характеристическое уравнение, имеющее n корней { x ₁, x ₂,..., x_n }. При подстановке их в систему, получим n экземпляров системы, причем все они будут заведомо совместны (разрешимы). В качестве решения каждая такая система будет давать набор коэффициентов для одной из МО. Энергии соответствующих орбиталей легко рассчитать через значения корней: e _i = a – b • х_i. Этим и исчерпывается общая схема решения Хюккелевской задачи.

Для иллюстрации рассмотрим несколько простых примеров.

ЭТИЛЕН

Электроны p-типа в молекуле этилена описываются двухцентровыми МО, построенными в виде линейной комбинации всего двух атомных орбиталей, причем обе атомные орбитали одинаковы (р -типа):

p ₁ = С _{1 а} p_a + C _{1 b} p_b

p ₂ = С _{2 а} p_a + C _{2 b} p_b

Уравнения Рутана имеют простой вид:

Запишем характеристическое уравнение: х ² – 1 = 0, откуда получим два корня: х ₁ = +1 и х ₂ = –1.

При подстановке первого корня в систему получим:

Отсюда следует, что коэффициенты первой МО равны по величине, но противоположны по знаку: С_a = – C_b, и из условия нормировки найдем их абсолютные величины: С _{1 a} = (0,5)^1/2 и C _{1 b} = – (0,5)^1/2. Аналогично, подставив в систему второй корень х ₂ = –1, найдем явный вид второй МО: С _{2 a} = (0,5)^1/2 и C _{2 b} = (0,5)^1/2.

Таким образом, МО молекулы этилена имеют вид:

а соответствующие им энергии равны:

e₁ = a – b • х ₁ = a – b e₂ = a – b • х ₂ = a + b

С математической точки зрения, задача полностью решена. Обсудим некоторые физические выводы из полученного решения.

Во-первых, зная величины энергий МО, мы можем построить корреляционную энергетическую диаграмму, которая показывает каким образом изменяются энергии стационарных состояний электронов при перекрывании атомных орбиталей, приводящему к образованию молекулярных орбиталей. При этом, надо иметь в виду, что оба интеграла (a и b) отрицательны, откуда следует, что энергия e₂ = a + b лежит ниже по шкале энергий, чемe₁ = a – b.

 

Из диаграммы ясно видно, что энергия одной из МО ниже энергии исходных атомных орбиталей, и ее заселение двумя электронами приведет к общему уменьшению энергии на величину D Е = 2 b. Следовательно, эта МО будет связывающей. Напротив, энергия другой МО выше энергии АО и ее заселение электронами привело бы к повышению общей энергии. Эта МО, следовательно, будет разрыхляющей. Можно легко определить, что переход одного из электронов со связывающей МО на разрыхляющую будет сопряжен с поглощением порции энергии D Е = 2 b, следовательно, такой переход будет происходить при облучении молекулы светом с частотой n = 2 b / h. Частоту перехода легко определить экспериментально. Это позволит оценить и величину резонансного интеграла b (около 16 ккал/моль или 65 кДж/моль).

Во-вторых, зная коэффициенты МО, мы можем построить графическое изображение МО и соответствующих им электронных облаков

Можно отметить две важные особенности найденных нами МО:

2 МО с более высокой энергией имеет дополнительную узловую поверхность, относительно МО с меньшей энергией,

2 МО могут быть охарактеризованы определенной симметрией, которая совпадает с симметрией всей молекулы этилена, так как полученные нами орбитали относятся к каноническому типу.

Подчеркнем, что используя менее грубые приближения, мы можем получить более точную форму МО и их энергии. Тем не менее, узловая структура и симметрия МО, полученных самым грубым методом МОХ, в точности такая же, как и у самосогласованных МО, получаемых самым точным методом Хартри-Фока. Поэтому многие результаты, получаемые в рамках МОХ, отличаются полной надежностью, что позволяет с успехом использовать простой метод Хюккеля для анализа многих важных задач, таких как, например, установление правил отбора в электронной спектроскопии и в химических реакциях (принцип сохранения орбитальной симметрии).

ЦИКЛОБУТАДИЕН

Хюккелевские МО в циклобутадиене образуются при суперпозиции 4‑х атомных орбиталей р -типа.

Уравнения Рутана и корни характеристического уравнения имеют следующий вид:

Здесь мы имеем случай двукратно вырожденного корня (х ₂ = х ₃). При решении системы для невырожденных корней никаких проблем не возникает, и мы легко находим коэффициенты соответствующих МО:

При подстановке вырожденного корня в систему уравнений получаем такой результат:

С_b + C_d = 0

C_a + C_c = 0

С_b + C_d = 0

C_a + C_c = 0

Видно, что набор из четырех неизвестных распадается на два поднабора, причем C_a = – C_c и С_b = – C_d. Поскольку поднаборы никак не связаны между собой, любая их линейная комбинация является решением системы:

Очевидно, что в данном случае (т.е. в случае вырожденных по энергии орбиталей) получилось целое двумерное пространство орбиталей, каждая из которых описывает возможное состояние электрона с энергией a. Для того, чтобы не перечислять все эти орбитали, мы можем выбрать из них две линейно независимые и взаимно ортогональные МО, которые будут играть роль базиса в этом двумерном пространстве.

Например, такой базис можно получить, если положить:

Возможны и другие варианты выбора базиса. Например, образуем еще один базис из предыдущего путем построения суммы и разности орбиталей p' и p'':

p ⁺ = (0,5)^1/2 [ p' + p'' ] p ^– = (0,5)^1/2 [ p' – p'' ]

Эти новые базисные орбитали будут иметь такие коэффициенты:

p ⁺ = 0,5 (p_a + p_b – p_с – p_d ) e ⁺ = a

p ^– = 0,5 (p_a – p_b – p_с + p_d ) e ^– = a

Обратим внимание на то, что с аналогичной ситуацией мы уже встречались при рассмотрении модели плоского ротатора. Там вырождение было связано с вращательным характером движения. В молекуле циклобутадиена ситуация точно такая же: поскольку скелет молекулы замкнут, электроны движутся в потенциальной яме почти цилиндрической формы, и описание данной системы качественно совпадает с описанием плоского ротатора. Подобная аналогичность описаний для внешне различных систем часто наблюдается в квантовой механике.

Общие решения

В некоторых случаях метод Хюккеля допускает формулировку общих решений для целых классов однотипных молекул. К таким классам относятся, например, линейные полиены и аннулены(циклические полиены).

ЛИНЕЙНЫЕ ПОЛИЕНЫ

Молекулы такого типа можно описать общей структурно-топологической формулой

Определитель Хюккеля для таких молекул имеет стандартный вид: по главной диагонали располагаются числа х, и кроме того,имеются две побочные диагонали (сверху и снизу от главной), состоящие из единиц. Остальные элементы равны нулю.

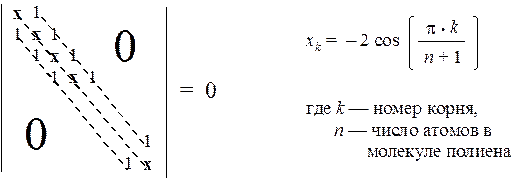
Это общее решение имеет простую графическую интерпретацию. Нарисуем полуокружность с радиусом 2 и разделим ее на (n + 1) равных частей n радиус-векторами. Проекции этих векторов на вертикальную ось и дадут искомые значения величин х_i, а следовательно, и вид энергетической диаграммы.

 

Легко заметить общую закономерность: все энергетические уровни линейных молекул лежат в узком интервале от a + 2 b до a – 2b, располагаясь, по мере увеличения числа атомов, все более и более тесно:

В пределе образуются две энергетические зоны, разделенные небольшой щелью. Такая структура, как известно, характерна для полупроводников. Действительно, очень длинные линейные полиены (полиацетилен) обладают полупроводниковыми свойствами.

Можно также заметить следующее: связывающие и разрыхляющие энергетические уровни располагаются симметрично, относительно атомного уровня (a). Для нечетных полиенов (нечетное число атомов) наблюдается, кроме того, один несвязывающий уровень.

Все рассмотренные особенности обусловлены топологическим характером метода МОХ.

Общее решение существует и для коэффициентов МО:

Для этого решения также можно найти графическую интерпретацию. Для каждой МО рассчитаем набор углов:

q _{k n} = (p • k • n) / (n + 1)

Теперь построим для каждого такого угла (угол нужно отсчитывать от горизонтальной оси) радиус-вектор в круге радиусом R = [2 / (n + 1)]^1/2. Проекции этих векторов на вертикальную ось и дадут величины коэффициентов С_kn.

Рассмотрим для примера молекулу бутадиена. Здесь имеется 4 атома и, следовательно, должно быть 4 МО.

При k = 1 углы равны: q_1n = p/5; 2p/5; 3p/5; 4p/5. Приближенные значения коэффициентов таковы:

{0,372 0,602 0,602 0,372}.

Соответствующую МО можно схематически изобразить так:

При k = 2 углы равны: q_2n = 2p/5; 4p/5; 6p/5; 8p/5. Приближенные значения коэффициентов таковы:

{0,602 0,372 – 0,372 – 0,602}.

Соответствующую МО можно схематически изобразить так:

 

 

k = 3. q_3n = 3p/5; 6p/5; 9p/5; 12p/5.

Приближенные значения

коэффициентов таковы:

{0,602 – 0,372 – 0,372 0,602}.

Соответствующую МО можно

схематически изобразить так:

 

 

k = 4. q_4n = 4p/5; 8p/5; 12p/5; 16p/5.

Приближенные значения

коэффициентов таковы:

{0,372 – 0,602 0,602 – 0,372}.

Соответствующую МО можно

схематически изобразить так:

 

Достаточно очевидно, что наблюдается симметрия: С ₁₁ = С ₁₄ и С ₁₂ = С ₁₃.

Можно заметить, что огибающие совокупности АО весьма напоминают отрезки синусоид, которые мы получали для простой модели “частица в ящике”. Эта аналогия, конечно, не случайна. Действительно, электроны в молекуле бутадиена заперты в одномерном ящике, стенки которого создаются электрическими полями ядер молекулы. Очевидно, что и в этом случае выполняется общее правило: чем больше узлов — тем выше энергия.

Циклические полиены (аннулены).

Определитель Хюккеля имеет точно такой же вид, как и для линейных молекул, за исключением двух единиц в вернем правом и нижнем левом углах, которые отражают факт замыкания цепи атомов в кольцо.

 

 

Графическая интерпретация решений выглядит так. Построим круг радиуса 2 и разделим его на N равных частей радиус-векторами, первый из которых ориентирован точно вниз. Тогда проекция вектора на вертикальную ось даст величину корня х_к.

 

 

 

 

Из этих диаграмм ясно видно основное отличие циклических систем: энергетические уровни являются дважды вырожденными (за исключением самого нижнего у всех циклов и самого верхнего у четных циклов).

Эта характерная особенность циклических структур приводит к тому, что число связывающих МО у них всегда нечетное (2 n + 1). Их полная электронная емкость равна 2(2 n + 1) = 4 n + 2, где n — любое целое число. Если число электронов в циклическом полиене равно 4 n + 2, то все его связывающие орбитали полностью заселены, а все разрыхляющие — свободны. Такая структура должна обладать особенно низкой энергией и быть особенно инертной в химическом отношении. Они называются ароматическими (по Хюккелю) структурами. Соответственно, условие ароматичности (4 n + 2) называется “правилом Хюккеля”.

Напротив, если число электронов в аннулене можно выразить как 4 n, то два из этих электронов будут располагаться на паре вырожденных МО, в соответствии с правилом Хунда. В результате, молекула приобретет электронную конфигурацию бирадикала и будет отличаться повышенной химической активностью. Такие структуры называются антиароматическими (по Хюккелю). Приведем несколько примеров.

Ароматические молекулы и ионы.

N = 3 4 5 6 7

n = 2 2 6 6 6

 

Для получения антиароматических систем с той же структурой достаточно изменить число электронов — добавить или отнять два электрона. Так, например, циклопропенил-анион и циклопентадиенил-катион будут представлять собой антиароматические структуры, в отличие от циклопропенил-катиона и циклопентадиенил-аниона.

Заметим также, что описанное определение ароматичности и антиароматичности не является единственно возможным. Известны и другие варианты этого понятия, основанные на иных признаках.

Коэффициенты МО в аннуленах могут быть единообразно выражены через комплексные числа типа:

 

Рассмотрим пример трехчленного цикла. Матрица коэффициентов МО будет выглядеть так:

 

 

С учетом того факта, что комплексная экспонента является периодической функцией и повторяется через интервал 2p, и что при значениях фазы, кратных 2p, она вырождается в 1, можно преобразовать эту матрицу к эквивалентному, но более простому виду:

 

 

Отсюда видно, что МО, соответствующая невырожденному уровню с наименьшей энергией, имеет действительные коэффициенты, тогда как МО, соответствующие вырожденному уровню, имеют коэффициенты в виде попарно сопряженных комплексных чисел. Это позволяет построить из комплексных МО действительные линейные комбинации, которые будут описывать возможные МО с тем же самым значением энергии. Построим эти комбинации в виде суммы и разности p₁ и p₂:

p⁺ = (1/2)^0,5 (p₁ + p₂) =

= (1/6)^0,5 { e i(2p/3)+ e i(-2p/3); e i(-2p/3)+ e i(2p/3); 1 + 1 } =

= (1/6)^0,5 {2 cos(2p/3); 2 cos(2p/3); 2} = (1/6)^0,5 {-1; -1; 2}.

Аналогично получим и вторую комбинацию:

 

 

Таким образом, набор коэффициентов действительных МО можно записать в виде матрицы:

 

 

 

Для такого представления МО можно построить и графические изображения самих МО и соответствующих им электронных облаков

 

 

 

 

p^о p^– p⁺

 

Пунктиром показано расположение узловых плоскостей. Видно, что обе вырожденные по энергии МО имеют одинаковое число узлов.

Рассмотренное преобразование комплексных МО в действительные возможно для любого аннулена. Если пронумеровать МО квантовым числом l, в соответствии со следующей схемой, то можно записать формулы для расчета коэффициентов действительных МО в общем виде.

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: