 |
Методика формирования математического понятия
|
|
|
|
Формирование понятия – сложный психологический процесс, протекающий часто по следующей схеме: ощущение → восприятие → представление → понятие. Таким образом, процесс формирования понятия разделен на две ступени: чувственную и логическую.
Существуют два подхода к введению понятия и его определения: индуктивный и дедуктивный. Рассмотрим индуктивный подход, который предполагает формирование понятия в соответствии со следующими этапами.
Этапы формирования понятия
1. Актуализация знаний и умений учащихся, необходимых для усвоения понятия.
Цель: создание условий для восприятия учебного материала, осуществление обратной связи между учителем и учащимися.
2. Мотивация
(показ необходимости изучения понятия, его значимости в жизни, в науке, в различных учебных дисциплинах)
Цель: создание условий для формирования личностно–значимого знания.
Средства для их реализации
Система целесообразно составленных вопросов и заданий для повторения необходимого материала.
Убедительные жизненные примеры, иллюстрирующие необходимость изучения нового понятия; проблемная ситуация, разрешение которой основано на использовании нового понятия.
3. Выделение существенных свойств понятия.
Цель: создание образов, адекватных формируемому понятию.
4. Синтез выделенных свойств, формулировка определения понятия
Цель: введение определения.
5. Работа над определением.
Цель: усвоение определения понятия
5.1. Усвоение формулировки
5.2. Анализ логический структуры определения.
5.3 Распознавание объектов по определению.
6. Изучение следствий из определения понятия (его свойств).
|
|
|
Цель: формирование понятия.
Примеры разнообразных моделей, обладающих такими свойствами.
Упражнения на построение объектов, удовлетворяющих указанным свойствам.
Упражнения на заполнение пропусков в формулировке определения, на нахождение ошибок в некорректных определениях.
Упражнения, способствующие выявлению логической структуры определения.
Упражнения на распознавание объектов, принадлежащих объёму понятия.
Учебные задачи на применение изученных свойств.
7. Изучение признаков понятия.
Цель: формирование понятия.
Учебные задачи на применение изученных признаков, в том числе на переформулировку определения понятия.
8. Установление связей изученного
понятия с другими понятиями.
Конструирование родословной понятия; его включение в существующую классификацию,
например, с помощью кругов Эйлера; задачи, в которых понятие используется в связи
с ранее изученными.
Формирование понятия дедуктивным методом осуществляется по следующему плану:
1. Формулировка определения нового понятия.
2. Рассмотрение частных и особых случаев выражения этого понятия.
3. Иллюстрация введённого понятия на конкретных примерах.
4. Изучение свойств и признаков понятия.
5. Аспекты применения понятия.
Отметим, что индуктивный метод применяется в старших классах, в
вузовской практике, а индуктивный – чаще используется в младших и средних классах.
Литература
1. Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. Н.Л. Стефановой. – М., Дрофа, 2005.
2.Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев, - М.: Просвещение, 2002.
3. Методика преподавания математики в средней школе: общая методика, Учеб. пособие для студентов пед. ин-тов / составители Р. С. Черкасов, А. А. Столяр. – М., Просвещение, 1985.
|
|
|
Теоремы и методика их изучения в курсе геометрии средней школы
Теоремы и их виды
Связь между понятиями устанавливается с помощью суждений. Суждением принято называть предложение, в котором выражается мысль о предмете, объекте, явлении. Существуют два основных свойства суждения: что-то утверждать или отрицать, быть истинным или ложным.
Выделяются следующие виды суждений:
· общеутвердительное (образуется с помощью кванторных слов: всякий, любой);
· частно утвердительное (образуется с помощью кванторных слов: существуют, некоторые);
· общеотрицательное (образуется с помощью кванторных слов: ни один, никакой, не существует);
· частно отрицательное (образуется с помощью кванторных слов: не всякий, не любой).
Часто кванторные слова опускаются, считается, что они понятны из смысла всего предложения.
Например,
«все квадраты суть прямоугольники» - общеутвердительное суждение; «некоторые треугольники равнобедренные» - частно утвердительное суждение;
«не существует рационального числа, квадрат которого равен 2» - общеотрицательное суждение;
«не любое натуральное число – чётное» - частно отрицательное суждение.
Математическим предложением называют повествовательное предложение, выражающее общеутвердительное или общеотрицательное суждение о математических объектах.
Под теоремой принято понимать математическое предложение (утверждение), истинность которого доказывается.
Таким образом, родословную понятия «теорема» можно охарактеризовать «цепочкой» понятий: теорема→математическое предложение→ суждение.
Запись теоремы состоит из формулировки (суждения, утверждения) и доказательства.
Виды формулировки теоремы
Формулировка теоремы может быть категорической или условной. Для условной формы характерны слова «если…, то…». Например, «если в параллелограмме диагонали равны, то параллелограмм является прямоугольником». Теорема «сумма углов треугольника равна 180°» сформулирована в категорической форме.
В формулировке каждой теоремы можно выделить условие (то, что дано) и заключение (то, что требуется доказать). Если теорема сформулирована в условной форме, то между словами «если…, то» содержится её условие, после слова «то» - заключение. Пусть Р – условие теоремы, а Q – её заключение. Тогда символически теорему можно записать в виде Р Þ Q (если Р, то Q). При выделении условия и заключения в теореме, сформулированной в категорической форме, нет такой ясности. Поэтому целесообразно научить школьников переходить от условной к категорической формулировке теоремы. Так, приведённую выше теорему можно переформулировать: «если данная фигура – треугольник, то сумма его углов равна 180°».
|
|
|
Из данной теоремы (1) могут быть образованы ещё три утверждения. Поменяем местами условие и заключение. Получим обратное утверждение (2) Q Þ Р (если Q, то Р). Оно может быть истинным (тогда это обратная теорема) или ложным. Заменим условие и заключение теоремы на их отрицание. Получим противоположное утверждение (3)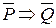 
(если не Р, то не Q). Оно также может быть либо истинным (теоремой), либо ложным. Наконец, может быть составлено контрапозитивное утверждение вида (4) 
.
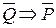Например, из теоремы «если углы вертикальны (Р), то они равны (Q)» (1) можно образовать следующие утверждения:
«если углы равны (Q), то они вертикальны (Р)» (2);
«если углы не вертикальны (
), то они не равны (
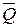)» (3);
«если углы не равны (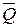),то они не вертикальны ()» (4).
Утверждения (1) и (4) истинны, а (2) и (3) – ложны. В математической логике доказывается, что утверждения (1) и (4), (2) и (3) равносильны, то есть их таблицы истинности совпадают. Схематически это можно изобразить так:
Аналогичным примером из алгебры является теорема «если каждое слагаемое делится на число, то и сумма делится на это число». Теорема «если в четырёхугольнике суммы противоположных сторон равны, то в него можно вписать окружность» служит примером истинности всех четырех утверждений.
Необходимое и достаточное условия
Пусть теорема сформулирована в виде Р Þ Q (если Р, то Q). Тогда Q называют необходимым условием Р, а Р – достаточным условием Q. Ясно, что Q – необходимое и достаточное условие Р, если обратное утверждение является истинным. Например, равенство углов является необходимым условием их вертикальности, а вертикальность углов является достаточным условием их равенства. При этом равенство углов не является необходимым и достаточным условием их вертикальности, так как обратное утверждение не является истинным. Равенство сумм противоположных углов четырёхугольника является необходимым и достаточным условием того, что в него можно вписать окружность. Подчёркивая этот факт, теорему формулируют в виде «для того, чтобы в четырёхугольник можно было вписать окружность необходимо и достаточно, чтобы суммы его противоположных сторон были равны». При этом доказывается истинность необходимого и достаточного условий. Доказывая необходимость, следует выделенное условие поставить в заключение теоремы.
|
|
|
Необходимость.
Дано: четырёхугольник; окружность, вписанная в четырёхугольник.
Доказать:суммы противоположных сторон четырёхугольника равны.
Затем докажем истинность обратной теоремы и тем самым докажем достаточность.
Достаточность.
Дано:суммы противоположных сторон четырёхугольника равны.
Доказать: в четырёхугольник можно вписать окружность.
Если некоторое условие Q является необходимым и достаточным условием Р, то его называют критерием Р. Так, равенство сумм противоположных сторон четырёхугольника является критерием того, что в него можно вписать окружность.
Доказательство теоремы
Процесс доказательства является предметом изучения логики, Мы рассмотрим некоторые аспекты, относящиеся к доказательству теорем в школе.
Одним из основных элементов доказательства теорем является умозаключение. Умозаключение есть мыслительная операция, в результате которой из одного или нескольких суждений, находящихся в определённой смысловой взаимной связи, получается новое суждение. По отношению к исходным суждением оно содержит новое знание. Исходные суждения – это посылки, полученное новое суждение – это вывод.
При доказательстве теорем в школьном курсе математики наиболее часто используется умозаключение, называемое силлогизмом. Оно имеет следующее строение:
Все М суть Р (большая посылка)
Все S суть М (малая посылка)
S суть Р (вывод)
|
Доказательство теоремы – это цепочка последовательно связанных силлогизмов, устанавливающих её истинность. При этом посылками силлогизмов могут быть аксиомы, теоремы, определения.
В качестве примера рассмотрим доказательство теоремы: «при пересечении двух параллельных прямых секущей соответственные углы равны».
Дано: а || b. c – секущая,
Доказать: Ð1=Ð2.
|
|
|
1 силлогизм:
Б.П.: Вертикальные углы равны.
М.П.: Ð1 и Ð3 –вертикальные.
В.: Ð1 = Ð3
2 силлогизм:
Б.П.: При пересечении двух параллельных прямых третьей внутренние накрест лежащие углы равны.
М. П.: Ð2 и Ð3 – внутренние накрест лежащие.
В.: Ð2 = Ð3
3 силлогизм.
Б.П. Если правые части равенства равны, то равны и левые части.
М.П.: Ð1 = Ð3, Ð2 = Ð3.
В.: Ð1=Ð2.
Существуют и другие правила вывода, например, отрицания,
контрапозиции.
Все доказательства можно разделить на прямые и косвенные. При прямом доказательстве задача состоит в том, чтобы подыскать такие утверждения, из которых по правилам вывода прийти к заключению теоремы. Доказательство, которое основывается на установлении истинности посредством опровержения некоторых суждений, называется косвенным. К косвенным доказательствам относится метод доказательства от противного или разделительный метод. Описание названных методов рассмотрите по учебному пособию [2, стр. 82].
|
|
|
