 |
Методы обучения математике
|
|
|
|
Под методами обучения будем понимать упорядоченные способы взаимосвязанной деятельности учителя и учащихся, направленные на достижение целей обучения.
Такой подход включает методы обучающей деятельности учителя (методы преподавания), методы познавательной деятельности ученика (методы изучения) и способы, посредством которых обучающая деятельность учителя управляет познавательной деятельностью ученика.
Под методами преподавания математики понимают способы передачи учащимся определённой системы математических знаний, умений и навыков.
К методам преподавания относятся лекция, рассказ, инструкция по работе с учебником, выполнению лабораторной или практической работы и другие. К методам преподавания следует обращаться тогда, когда учащиеся должны научиться действовать по «образцу» или в случае, когда они не способны усвоить материал самостоятельно. Например, нет подходящего источника изучения или он слишком сложен.
Под методами изучения математики понимают способы осуществления активной, самостоятельной деятельности математического характера самих школьников. Среди методов изучения математики условно выделяют научные и учебные методы.
К научным методам относятся:
· наблюдение и опыт (эксперимент);
· сравнение и аналогия;
· обобщение и абстрагирование;
· анализ и синтез;
· индукция и дедукция.
Перечисленные методы применяются в научных исследованиях, они служат средством приобретения новых знаний в науке. Естественно их использование в адаптированной (приспособленной) для этого форме в процессе познания учащегося.
Учебные методы изучения математики специально созданы в методике с целью эффективного изучения предмета. Назовём среди них эвристический метод, метод обучения на моделях, метод программированного обучения.
|
|
|
Представим приведённую классификацию методов схематически.
Отметим, что в практике обучения методы преподавания и изучения прочно взаимосвязаны, и разделить их не всегда удаётся. Остановимся более подробно на названных научных методах.
Наблюдение и опыт
Наблюдением называется метод изучения объектов и явлений окружающего мира в их естественных условиях. Под опытом (экспериментом) понимают такой метод изучения предметов и явлений, который предполагает вмешательство в их естественное состояние, создание искусственных условий, разделение на части, соединение с другими объектами и явлениями. Всякий опыт связан с наблюдением. Они должны быть направлены на создание специальных ситуаций, чтобы предоставить учащимся возможность выявить очевидные закономерности, факты, идеи доказательства.
Например, наблюдая чертежи, можно согласиться с разумностью следующих утверждений:
· через любые две различные точки плоскости проходит единственная прямая;
· прямая делит плоскость на две полуплоскости;
· если две различные точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости;
· простые числа в ряду натуральных чисел распределены неравномерно;
· если дискриминант квадратного трёхчлена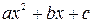 
отрицателен, то функция 
принимает постоянные по знаку значения.
С помощью опыта, состоящего в разрезании треугольника, можно
показать учащимся, что сумма углов треугольника равна 180°
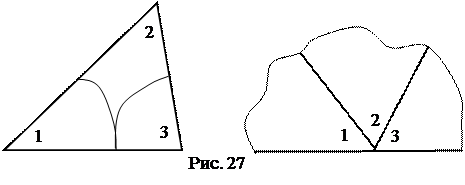
Если на листе бумаги провести прямую линию, нанести цветную капельку, перегнуть лист по начерченной прямой и прогладить рукой половинки, то развернув лист, можно наблюдать фигуры, симметричные относительно прямой. С помощью прибора, изобретённого в 1603 году Христофором Шейнером, и названного пантографом, можно наблюдать подобные фигуры.
|
|
|
Названные методы помогают самостоятельному открытию учащимися математических фактов, они служат эвристическим средством. Особую роль эти методы играют в младших классах. К недостаткам их следует отнести то, что ни один из них не является средством доказательства.
Сравнение и аналогия
Сравнение математических фигур и величин
служит материалом для игр и обучения мудрости
Песталоцци И.Г.
В дидактике сравнение должно быть основным
приёмом
Ушинский К.Д.
Сравнение – мысленное установление сходств и различий объектов изучения. Например, сравнение параллелограмма и трапеции позволяет выделить их общие свойства: они оба четырёхугольники, оба имеют параллельные стороны, - и различие: в одном две пары параллельных сторон, в другом – одна. Сравнение обыкновенных и алгебраических дробей выявляет их сходство: наличие числителя и знаменателя, отсутствие значения, когда знаменатель обращается в нуль и различие: в одном случае числитель и знаменатель – числа, в другом алгебраические выражения.
Сравнение как метод исследования широко применяется в математике не только для изучения математических свойств объекта, но и для установления самих этих свойств. В этом смысле особую роль играет аналогия – сравнение
по сходству. Рассуждение по аналогии состоит в следующем: если два предмета или явления имеют какие–то общие признаки, то, вероятно, они могут иметь и другие общие признаки.
Схематически:
Объёкт А имеет признаки а, в, с,х.
Объёкт В имеет признаки а, в, с.
Заключение по аналогии: вероятно объект В имеет признак х.
Заключение по аналогии следует доказать или опровергнуть.
Рассмотрим примеры рассуждений по аналогии.
По теореме Пифагора квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах. Все квадраты подобны. Построим подобные многоугольники (на рисунке подобные треугольники) на гипотенузе и катетах так, чтобы 
сходственными сторонами этих многоугольников служили стороны 
треугольника.
Сформулируем утверждение, аналогичное теореме Пифагора: многоугольник, построенный на гипотенузе равновелик сумме подобных многоугольников, построенных на катетах. Дополнительные исследования показывают, что это верно. Распространим приведённую аналогию на кубы с ребрами, равными гипотенузе и катетам данного прямоугольного треугольника. Аналогичное утверждение о равновеликости куба, построенного на гипотенузе и суммы кубов, построенных на катетах, оказывается неверным: пусть с – гипотенуза треугольника, а и в – его катеты, тогда с > а, | a 2
|
|
|
+ с > в; | b 2
ca 2+ c b 2> a 3+ b 3, c (a 2+ b 2) > a 3+ b 3, c3 > a 3+ b 3.
Аналогия имеет широкое применение в в процессе обучения математике. Приведём пример. Параллелепипед – пространственный аналог параллелограмма. В параллелограмме противоположные стороны параллельны, в параллелепипеде противоположные грани параллельны. Рассуждая по аналогии, можно прийти к гипотезе, что в параллелепипеде также как и в параллелограмме, диагонали, пересекаясь, делятся точкой пересечения пополам. Но если видеть только сходство и не замечать различия, в частности, что в параллелограмме всего две диагонали, а в параллелепипеде - четыре, то мы упустим важное свойство, подлежащее доказательству: все диагонали параллелепипеда пересекаются в одной точке.
Следовательно, применению аналогии должно предшествовать сравнение, с помощью которого выделяется как сходство, так и различие.
Используя аналогию, в школе изучают натуральные числа и десятичные дроби, обыкновенные и алгебраические дроби, сферу и окружность, круг и шар... Иногда аналогия оказывает «медвежью услугу» Так, по аналогии с верным свойством арифметических корней 
учащиеся используют свойство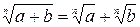 
, в неверности которого их можно убедить, например, для а = 9, в = 16. Такие примеры «вредных» аналогий можно продолжить. Однако полезность аналогий позволяла великому немецкому математику и астроному Иоганну Кеплеру писать: «И я больше всего дорожу Аналогиями, моими самыми верными учителями. Они знают все секреты Природы, и им меньше всего следует пренебрегать в Геометрии».
|
|
|
