 |
Уравнения однородной линии в стационарном режиме
|
|
|
|
Под первичными параметрами линии будем понимать сопротивление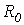 
, индуктивность 
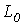, проводимость 
и емкость 
, отнесенные к единице ее длины. Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины 
со структурой, показанной на рис. 1.
Пусть напряжение и ток в начале такого элементарного четырехполюсника равны u и i, а в конце соответственно 
и 
.
Разность напряжений в начале и конце участка определяется падением напряжения на резистивном и индуктивном элементах, а изменение тока на участке равно сумме токов утечки и смещения через проводимость и емкость. Таким образом, по законам Кирхгофа
или после сокращения на
 ;
| (1) |
 .
| (2) |
Теорию цепей с распределенными параметрами в установившихся режимах будем рассматривать для случая синусоидального тока. Тогда полученные соотношения при 
можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока.
Вводя комплексные величины и заменяя 
на 
, на основании (1) и (2) получаем
 ;
| (3) |
 ,
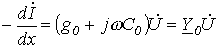| (4) |
где 
и 
- соответственно комплексные сопротивление и проводимость на единицу длины линии.
Продифференцировав (3) по х и подставив выражение 
из (4), запишем
.
Характеристическое уравнение
,
откуда
.
Таким образом,
 ,
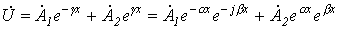| (5) |
где 
- постоянная распространения; 
- коэффициент затухания; 
- коэффициент фазы.
Для тока согласно уравнению (3) можно записать
 ,
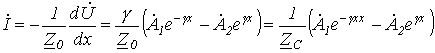| (6) |
где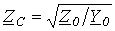 
- волновое сопротивление.
Волновое сопротивление 
и постоянную распространения 
называют вторичными параметрами линии, которые характеризуют ее свойства как устройства для передачи энергии или информации.
|
|
|
Определяя 
и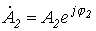 
, на основании (5) запишем
 .
| (7) |
Аналогичное уравнение согласно (6) можно записать для тока.
Слагаемые в правой части соотношения (7) можно трактовать как бегущие волны: первая движется и затухает в направлении возрастания х, вторая – убывания. Действительно, в фиксированный момент времени каждое из слагаемых представляет собой затухающую (вследствие потерь энергии) гармоническую функцию координаты х, а в фиксированной точке – синусоидальную функцию времени.
Волну, движущую от начала линии в сторону возрастания х, называют прямой, а движущуюся от конца линии в направлении убывания х – обратной.
На рис. 2 представлена затухающая синусоида прямой волны для моментов времен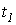и 
и 
. Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения по линии неизменного фазового состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны:
 .
| (8) |
Продифференцировав (8) по времени, получим
 .
| (9) |
Длиной волны 
называется расстояние между двумя ее ближайшими точками, различающимися по фазе на 
рад. В соответствии с данным определением
,
откуда
и с учетом (9)
.
В соответствии с введенными понятиями прямой и обратной волн распределение напряжения вдоль линии в любой момент времени можно трактовать как результат наложения двух волн: прямой и обратной, - перемещающихся вдоль линии с одинаковой фазовой скоростью, но в противоположных направлениях:
 ,
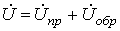| (10) |
где в соответствии с (5) 
и.
Представление напряжения в виде суммы прямой и обратной волн согласно (10) означает, что положительные направления напряжения для обеих волн выбраны одинаково: от верхнего провод 
а к нижнему.
Аналогично для тока на основании (6) можно записать
 ,
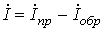| (11) |
где 
и 
.
Положительные направления прямой и обратной волн тока в соответствии с (11) различны: положительное направление прямой волны совпадает с положительным направлением тока 
(от начала к концу линии), а положительное направление обратной волны ему противоположно.
|
|
|
На основании (10) и (11) для прямых и обратных волн напряжения и тока выполняется закон Ома
| ; |  .
|
Рассмотрим теоретически важный случай бесконечно длинной однородной линии.
Бесконечно длинная однородная линия. Согласованный режим работы
В случае бесконечно длинной линии в выражениях (5) и (6) для напряжения и тока слагаемые, содержащие 
, должны отсутствовать, т.к. стремление 
лишает эти составляющие физического смысла. Следовательно, в рассматриваемом случае 
. Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным
| ; | 
| . | (12) |
На основании соотношений (12) можно сделать важный вывод, что для бесконечно длинной линии в любой ее точке, в том числе и на входе, отношение комплексов напряжения и тока есть постоянная величина, равная волновому сопротивлению:
.
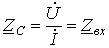Таким образом, если такую линию мысленно рассечь в любом месте и вместо откинутой бесконечно длинной части подключить сопротивление, численно равное волновому, то режим работы оставшегося участка конечной длины не изменится. Отсюда можно сделать два вывода:
Уравнения бесконечно длинной линии распространяются на линию конечной длины, нагруженную на сопротивление, равное волновому. В этом случае также имеют место только прямые волны напряжения и тока.
У линии, нагруженной на волновое сопротивление, входное сопротивление также равно волновому.
Режим работы длинной линии, нагруженной на сопротивление, равное волновому, называется согласованным, а сама линия называется линией с согласованной нагрузкой.
Отметим, что данный режим практически важен для передачи информации, поскольку характеризуется отсутствием отраженных (обратных) волн, обусловливающих помехи.
Согласованная нагрузка полностью поглощает мощность волны, достигшей конца линии. Эта мощность называется натуральной. Поскольку в любом сечении согласованной линии сопротивление равно волновому, угол сдвига 
между напряжением и током неизменен. Таким образом, если мощность, получаемая линией от генератора, равна 
, то мощность в конце линий длиной 
в данном случае
|
|
|
,
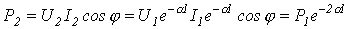откуда КПД линии
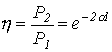
и затухание
.
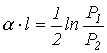Как указывалось при рассмотрении четырехполюсников, единицей затухания является непер, соответствующий затуханию по мощности в 
раз, а по напряжению или току – в 
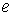раз.
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- В чем заключается разница между цепями с сосредоточенными и распределенными параметрами?
- По какому критерию цепь относят к классу цепей с распределенными или сосредоточенными параметрами?
- Нарисуйте схему замещения длинной линии.
- Объясните понятия прямой и обратной бегущих волн.
- Что такое согласованный режим работы цепи с распределенными параметрами, чем он характеризуется?
- Определить первичные параметры линии, если ее вторичные параметры
.
Ответ: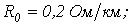 
- Определить по условиям предыдущей задачи КПД линии длиной 200 км, считая, что она нагружена на сопротивление, равное волновому.
Ответ: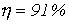 
.
- Определить , и для кабеля, у которого
, 
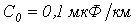, если частота 
.
Ответ: 
; 
; 
.
- По условиям предыдущей задачи определить длину волны и ее фазовую скорость.
Ответ: 
Лекция N 41
Линия без искажений
Пусть сигнал, который требуется передать без искажений по линии, является периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для составляющих его гармонических затухание и фазовая скорость различны, т.е. если последние являются функциями частоты. Таким образом, для отсутствия искажений, что очень важно, например, в линиях передачи информации, необходимо, чтобы все гармоники распространялись с одинаковой скоростью и одинаковым затуханием, поскольку только в этом случае, сложившись, они образуют в конце линии сигнал, подобный входному.
|
|
|
Идеальным в этом случае является так называемая линия без потерь, у которой сопротивление 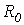и проводимость равны нулю.
Действительно, в этом случае
,
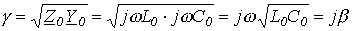т.е. независимо от частоты коэффициент затухания 
и фазовая скорость
.
Однако искажения могут отсутствовать и в линии с потерями. Условие передачи сигналов без искажения вытекает из совместного рассмотрения выражений для постоянной распространения
| (1) |
и фазовой скорости
 .
| (2) |
Из (1) и (2) вытекает, что для получения 
и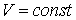 
, что обеспечивает отсутствие искажений, необходимо, чтобы 
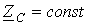, т.е. чтобы волновое сопротивление не зависело от частоты.
 .
| (3) |
Как показывает анализ (3), при
| (4) |
есть вещественная константа.
Линия, параметры которой удовлетворяют условию (4), называется линией без искажений.
Фазовая скорость для такой линии
и затухание
.
Следует отметить, что у реальных линий (и воздушных, и кабельных) 
. Поэтому для придания реальным линиям свойств линий без искажения искусственно увеличивают их индуктивность путем включения через одинаковые интервалы специальных катушек индуктивности, а в случае кабельных линий – также за счет обвивания их жил ферромагнитной лентой.
|
|
|
