Уравнения переходных процессов в цепях с распределенными параметрами

При рассмотрении схемы замещения цепи с распределенными параметрами были получены дифференциальные уравнения в частных производных

;

(5)

 

(6)

Их интегрирование с учетом потерь представляет собой достаточно сложную задачу. В этой связи будем считать цепь линией без потерь, т.е. положим и . Такое допущение возможно для линий с малыми потерями, а также при анализе начальных стадий переходных процессов, часто наиболее значимых в отношении перенапряжений и сверхтоков.

С учетом указанного от соотношений (5) и (6) переходим к уравнениям

(7)

 

(8)

Для получения уравнения (7) относительно одной переменной продифференцируем (7) по х, а (8) – по t:

;

(9)

 

.

(10)

Учитывая, что для линии без потерь , после подстановки соотношения (10) в (9) получим

.

(11)

Аналогично получается уравнение для тока

.

(12)

Волновым уравнениям (11) и (12) удовлетворяют решения

;

.

Как и ранее, прямые и обратные волны напряжения и тока связаны между собой законом Ома для волн

и ,

где .

При расчете переходных процессов следует помнить:

1. В любой момент времени напряжение и ток в любой точке линии рассматриваются как результат наложения прямой и обратной волн этих переменных на соответствующие величины предшествующего режима.
2. Всякое изменение режима работы цепи с распределенными параметрами обусловливает появление новых волн, накладываемых на существующий режим.
3. Для каждой волны в отдельности выполняется закон Ома для волн.

Как указывалось, переходный процесс в цепях с распределенными параметрами характеризуется наложением многократно отраженных волн. Рассмотрим многократные отражения для двух наиболее характерных случаев: подключение источника постоянного напряжения к разомкнутой и короткозамкнутой линии.

 

Переходные процессы при включении на постоянное напряжение
разомкнутой и замкнутой на конце линии

При замыкании рубильника (см. рис. 2) напряжение в начале линии сразу же достигает величины , и возникают прямые волны прямоугольной формы напряжения и тока , перемещающиеся вдоль линии со скоростью V (см. рис. 3,а).Во всех точках линии, до которых волна еще не дошла, напряжение и ток равны нулю.Точка, ограничивающая участок линии, до которого дошла волна, называется фронтом волны. В рассматриваемом случае во всех точках линии, пройденных фронтом волны, напряжение равно , а ток - .

Отметим, что в реальных условиях форма волны, зависящая от внутреннего сопротивления источника, параметров линии и т.п., всегда в большей или меньшей степени отличается от прямоугольной.

Кроме того, при подключении к линии источника с другим законом изменения напряжения форма волны будет иной. Например, при экспоненциальном характере изменения напряжения источника (рис. 4,а) волна будет иметь форму на рис. 4,б.

В рассматриваемом примере с прямоугольной волной напряжения при первом пробеге волны напряжения и тока (см. рис. 3,а) независимо от нагрузки имеют значения соответственно и , что связано с тем, что волны еще не дошли до конца линии, и, следовательно, условия в конце линии не могут влиять на процесс.

В момент времени волны напряжения и тока доходят до конца линии длиной l, и нарушение однородности обусловливает появление обратных (отраженных) волн. Поскольку в конце линия разомкнута, то

,

откуда и .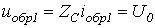

В результате (см. рис. 3,б) напряжение в линии, куда дошел фронт волны, удваивается, а ток спадает до нуля.

В момент времени , обратная волна напряжения, обусловливающая в линии напряжение , приходит к источнику, поддерживающему напряжение . В результате возникает волна напряжения 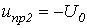и соответствующая волне тока (см. рис. 3,в).

В момент времени волны напряжения и тока подойдут к концу линии. В связи с ХХ и (см. рис. 3,г). Когда эти волны достигнут начала линии, напряжение и ток в ней окажутся равными нулю. Следовательно, с этого момента переходный процесс будет повторяться с периодичностью .

В случае короткозамкнутой на конце линии в интервале времени 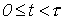картина процесса соответствует рассмотренной выше. При , поскольку в конце линии и , что приведет к возрастанию тока в линии за фронтом волны до величины . При от источника к концу линии будет двигаться волна напряжения и соответствующая ей волна тока , обусловливающая ток в линии, равный , и т. д. Таким образом, при каждом пробеге волны ток в линии возрастает на .

Отметим, что в реальном случае, т.е. при наличии потерь мощности, напряжение в линии в режиме ХХ постепенно выйдет на уровень, определяемый напряжением источника, а ток в режиме КЗ ограничится активным сопротивлением и проводимостью линии, а также внутренним сопротивлением источника.

 

Литература

1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
2. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

Контрольные вопросы и задачи

1. Какой характер имеет зависимость входного сопротивления линии от ее длины и почему?
2. С помощью чего можно изменять характер и величину входного сопротивления цепи с распределенными параметрами?
3. Какое допущение лежит в основе анализа переходных процессов в длинных линиях?
4. Каким законом связаны волны напряжения и тока в переходных режимах?
5. Линия без потерь имеет длину , фазовая скорость волны . При каких частотах в ней будут иметь место минимумы и максимумы входного сопротивления?

Ответ: .

1. При каких длинах линии без потерь в ней будут наблюдаться резонансные явления, если фазовая скорость равна скорости света, а частота ?

Ответ: .

1. Постройте эпюры распределения напряжения и тока вдоль линии, питаемой от источника постоянного напряжения, при включении и отключении в ее конце резистивной нагрузки.

Лекция N 43

Сведение расчета переходных процессов в цепях с распределенными
параметрами к нулевым начальным условиям

С учетом граничных условий расчет переходных процессов в цепях с распределенными параметрами можно проводить как при нулевых, так и ненулевых начальных условиях. Однако в первом случае анализ осуществляется в целом проще, что определяет целесообразность сведения расчета к нулевым начальным условиям. Пример такого сведения на основе принципа наложения для задачи на подключение в конце линии нагрузки схематично иллюстрирует рис. 1, где в последней схеме сопротивление имитирует входное сопротивление активного двухполюсника.

Таким образом, если к линии, в общем случае заряженной, подключается некоторый в общем случае активный двухполюсник, то для нахождения возникающих волн необходимо определить напряжение 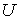на разомкнутых контактах ключа (рубильника), после чего рассчитать токи и напряжения в схеме с сосредоточенными параметрами, включаемой на это напряжение 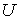при нулевых начальных условиях. Полученные напряжения и токи накладываются на соответствующие величины предыдущего режима.

При отключении нагрузки или участков линии для расчета возникающих волн напряжения и тока также можно пользоваться методом сведения задачи к нулевым начальным условиям. В этом случае, зная ток в ветви с размыкаемым ключом (рубильником), необходимо рассчитать токи и напряжения в линии при подключении источника тока противоположного направления непосредственно к концам отключаемой ветви. Затем полученные токи и напряжения также накладываются на предыдущий режим.

В качестве примера такого расчета рассмотрим длинную линию без потерь на рис. 2, находящуюся под напряжением , к которой подключается дополнительный приемник с сопротивлением .

В соответствии со сформулированным выше правилом схема для расчета возникающих при коммутации волн будет иметь вид на рис. 3. Здесь

;

и в соответствии с законом Ома для волн

.

Соответствующие полученным выражениям эпюры распределения напряжения и тока вдоль линии представлены на рис. 4.

Отметим, что, поскольку

,

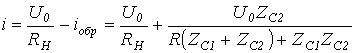к источнику от места подключения нагрузки пошла волна, увеличивающая ток на этом участке.

Если наоборот приемник с сопротивлением не подключается, а отключается, то расчет возникающих при этом волн тока и напряжения следует осуществлять по схеме рис.5.

 

Правило удвоения волны

Пусть волна произвольной формы движется по линии с волновым сопротивлением и падает на некоторую нагрузку (см. рис. 6,а).

Для момента прихода волны к нагрузке можно записать

;

(1)

или

.

(2)

Складывая (1) и (2), получаем

.

(3)

Соотношению (3) соответствует расчетная схема замещения с сосредоточенными параметрами, представленная на рис. 6,б. Момент замыкания ключа в этой схеме соответствует моменту падения волны на нагрузку в реальной линии. При этом, поскольку цепь на рис. 6,б состоит из элементов с сосредоточенными параметрами, то расчет переходного процесса в ней можно проводить любым из рассмотренных ранее методов (классическим, операторным, с использованием интеграла Дюамеля).

Следует отметить, что, если в длинной линии имеет место узел соединения других линий или разветвление, то в соответствии с указанным подходом эту неоднородность следует имитировать резистивным элементом с соответствующим сопротивлением, на который падает удвоенная волна.

Пусть, например, линия с волновым сопротивлением разветвляется на две параллельные линии с волновыми сопротивлениями и (см. рис. 7,а). Узел разветвления в расчетном плане эквивалентен резистивному элементу с сопротивлением

 

,

при этом расчетная схема замещения для момента прихода волны к стыку линий имеет вид на рис. 7,б.

Так, если падающая волна напряжения имеет прямоугольную форму и величину , то в соответствии со схемой замещения на рис. 7,б напряжение на стыке линий в момент прихода волны

.

Этой величине будут равны волны напряжения, которые пойдут далее в линии с волновыми сопротивлениями и . Отраженная же волна, которая пойдет по линии с волновым сопротивлением , будет характеризоваться напряжением

.

Таким образом, по правилу удвоения волны определяются отраженные (появившиеся в результате отражения от неоднородности) и преломленные (прошедшие через неоднородность) волны, расчет которых осуществляется по схемам замещения с сосредоточенными параметрами. Следовательно, методика расчета переходных процессов в цепях с распределенными параметрами состоит в последовательном составлении схем замещения с сосредоточенными параметрами для каждого момента прихода очередной падающей волны на очередную неоднородность и расчете по ним отраженных и преломленных волн.

В качестве примера рассмотрим падение прямоугольной волны напряжения величиной на включенный в конце линии конденсатор (см. рис. 8,а).

Для расчета напряжения на конденсаторе и тока через него в момент прихода волны к концу линии составим схему замещения с сосредоточенными параметрами (см. рис. 8,б). Для этой схемы можно записать

,

где .

Это напряжение определяется суммой прямой (падающей) и обратной (отраженной) волн, т.е.

,

откуда для отраженной волны имеет место соотношение

или для той же волны в произвольной точке линии с координатой , отсчитываемой от конца линии, с учетом запаздывания на время -

.

Соответственно для отраженной волны тока можно записать

.

Эпюры распределения напряжения и тока вдоль линии для момента времени , когда отраженная волна прошла некоторое расстояние , представлены на рис. 9. В этот момент напряжение на конденсаторе

и ток через него

.

В качестве другого примера рассмотрим падение прямоугольной волны напряжения величиной на включенный в конце линии индуктивный элемент (см. рис. 10,а). В соответствии с расчетной схемой на рис. 10,б для тока через катушку индуктивности и напряжения на ней соответственно можно записать

;

,

где

С учетом этого выражения для отраженных волн напряжения и тока в произвольной точке линии имеют вид

;

.

Эпюры распределения напряжения и тока вдоль линии для момента времени приведены на рис. 11.

 

Литература

1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
2. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

Контрольные вопросы и задачи

1. Как расчет переходных процессов в длинных линиях сводится к нулевым начальным условиям?
2. В чем смысл правила удвоения волн, для чего оно используется?
3. Сформулируйте методику расчета переходных процессов в цепях с распределенными параметрами.
4. Что называется отраженными и преломленными волнами?
5. В линии на рис. 2 , , . Определить волны тока и напряжения, возникающие при коммутации, если .

Ответ: ; ; .

1. Рассмотреть падение волны напряжения, возникшей при коммутации в схеме предыдущей задачи, на резистор 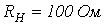и определить обратные волны тока и напряжения, образующиеся при этом падении.

Ответ: ; .

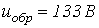1. К линии, находящейся под напряжением , подключается незаряженная линия (см. рис. 12). Определить волны тока и напряжения, возникающие при этой коммутации, если , .

Ответ: ; ; .

1. Рассмотреть падение волны напряжения при коммутации в схеме предыдущей задачи на резистор и определить возникающие при этом обратные волны напряжения и тока.

Ответ: ; .

1. Однородная длинная линия с нагружена на емкостный элемент с . Посередине линии параллельно ему включен еще один конденсатор с . От генератора вдоль линии распространяется волна напряжения, которую до падения на конденсатор можно считать прямоугольной с . Записать выражение для напряжения на конденсаторе .

Ответ: .

Долог путь поучений,

краток же и успешен

на примерах

В решении любой физической задачи можно выделить одни и те же действия.

Выполнение, сопровождаемое пояснениями, в ходе письменного экзамена (конкурса):

1. Прочесть текст задачи, выяснить основной вопрос задачи, выделить заданные и неизвестные величины.

2. Выделить систему рассматриваемых в задаче тел и состояния тел, заменить реальные тела идеальными объектами (точечный заряд, однородное поле, идеальный проводник). Сделать схематический рисунок (или несколько рисунков для каждого из рассматриваемых состояний тел).

3. Записать содержание задачи в краткой символической форме (столбик данных и неизвестных величин) с одновременным переводом числовых значений в СИ, помечая однородные величины, характеризующие разные тела или разные состояния тел индексами.

4. Установить, с помощью каких законов объясняется описанная в задаче ситуация, записать математические выражения этих законов и дополнительные соотношения, связывающие неизвестные и заданные величины.

5. Решить полученную систему уравнений в общем виде. (В редких случаях приходится проводить поэтапные вычисления, например, чтобы выяснить, возможен тот или иной физический процесс).

6. Проверить правильность решений путем действий с наименованиями единиц.

7. Вычислить точную величину, подставив в расчетную формулу числовые значения. (Действия 6 и 7 можно выполнять одновременно, подставляя в формулу значения величин вместе с их единицами).

8. Проанализировать полученные результаты.

9. Записать результаты решения в виде ответов на вопросы, поставленные в задаче.

НЕ ЗАБЫВАЙТЕ ПИСАТЬ ПОЯСНЕНИЯ ПО ХОДУ РЕШЕНИЯ!

 

Схема анализа решения

- Выяснить, какой физический смысл может иметь слагаемое правой части полученного уравнения;

- установить: как изменяется искомая величина с изменением тех величин, через которые она выражена;

- применить полученное в общем виде решение ко всем другим характерным случаям, представляющим другие варианты явления, описанного в данной задаче.

- Оценить правдоподобность результата.

Среди множества опубликованных пособий для подготовки к конкурсу по физике рекомендую выбрать следующие:

1. Мелешина А.М., Фосс М.А. Решайте задачи по физике, а мы вам поможем: книга для учащихся. - М.: Просвещение, 1994 - 207 с.

2. Конкурсные задачи по физике: Пособие для поступающих в вузы / А.Г. Андреев, Н.А. Гладков и др. М.: издательство МГТУ, 1993 - 144 с.

3. Парфенова Н.А., Фомина М.В. Решение задач по физике. В помощь поступающим в вузы. Часть 2. - М.: Мир, 1993 - 206 с.

4. Меледин Г.В. Физика в задачах: Экзаменационные задачи с решениями: учебное пособие. - М.: Наука, Гл. ред. физ.-мат. лит., 1985 - 208 с.

5. Таралов Л.В., Тарасова А.Н. Вопросы и задачи по физике (анализ характерных ошибок поступающих в вузы). Учебное пособие. - М.: Высшая школа, 1975 - 253 с.

Ни одно из перечисленных пособий не замещает школьных учебников, но может быть использовано как дополнение к ним.

Формулы-определения и формулы-законы

в разделе "Электричество"

Электростатика

Определения величин	Основные законы
- напряженность электрического поля, В/м - потенциал, В - разность потенциалов, В - электроемкость проводника, Ф - электроемкость конденсатора, Ф - диэлектрическая проницаемость среды.	Закон сохранения электрического заряда. Закон сохранения энергии. Принцип суперпозиции электрических полей: Закон Кулона , Н Напряженность поля точечного заряда , В/м Потенциал поля точечного заряда , В Связь напряженности и потенциала , В/м Электроемкость плоского конденсатора , Ф Энергия электрического поля, Дж

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1 на закон сохранения заряда.

Два одинаковых металлических шарика с зарядами q₁=20 нКл и q₂=-40 нКл вследствие взаимного притяжения соприкоснулись и снова разошлись на такое же расстояние. Сравнить силы взаимодействия шариков до и после соприкосновения. Изменится ли энергия данной системы зарядов?

F₂<F₁? W_эл=const?

q₁=2010^-9 Кл, q₂=-4010^-9 Кл, r₁=r₂=r,

Решение.

В начальном состоянии потенциалы шариков различны, а электроемкости зарядов одинаковы. Из определения электроемкости получаем

Когда шарики соприкасаются, заряды шариков перераспределяются до тех пор, пока потенциалы тел не уравниваются. В условиях равновесия зарядов поверхность проводника представляет собой эквипотенциальную поверхность. Это достигается путем перехода части заряда от тела с более высоким к телу к более низким потенциалом. Заряды тел так же становятся одинаковыми и по модулю и по знаку, q'₁=q'₂.

Считая систему тел замкнутой, получим по закону сохранения электрического заряда:q₁+q₂=q'₁+q'₂.

После соприкосновения заряд распределится поровну между шариками q'₁=q'₂=(q₁+q₂)/2=-1010^-9Кл.

Силы взаимодействия шариков в начальном и конечном состояниях:

и

Расстояние r одинаково в обоих состояниях, и k=const, поэтому для ответа на первый вопрос задачи достаточно сравнить произведения зарядов 20(-40)>(-10) (-10), отсюда получаем

F1>F2.

Модуль силы уменьшается, но при этом знак величины сменился на противоположный, то есть притяжение сменилось отталкиванием.

Энергия системы зарядов равна: где - потенциал электрического поля в том месте, где находится заряд q_i.

В нашем случае:

как видим, энергия системы зарядов зависит так же, как сила их взаимодействия, от произведения зарядов. Модуль этого произведения, как уже показано, уменьшается.

Нет ли здесь нарушения закона сохранения энергии? Ответ на этот вопрос несколько выходит за рамки электростатики. Дело в том, что их потенциалы выравниваются, заряды приходят в движение, то есть возникает кратковременный электрический ток. Это приводит к нагреванию проводников и излучению квантов электромагнитной энергии в окружающую среду. В этом смысле наша система из двух заряженных шариков не замкнутая. В то же время алгебраическая сумма зарядов не изменяется, так как заряды не вносятся и не выносятся из системы (кванты не имеют заряда), в этом смысле система замкнута и закон сохранения заряда выполняется.

Пример 2 на закон сохранения заряда

Два плоских воздушных конденсатора равной емкости соединили параллельно, зарядили до 300 В и отключили от источника. Какой станет разность потенциалов на обкладках конденсаторов, если один из них погрузить в керосин?

U'=?; U=300 B, C₁=C₂=C, e₁=e₂=1, e'₁=1, e'₂=39.

Решение.

При параллельном соединении конденсаторов разность потенциалов обкладок у обоих конденсаторов одинакова U=U₁=U₂. После погружения в диэлектрик второго конденсатора U'=U'₁=U'₂ напряжение на обоих конденсаторах переменится, но алгебраическая сумма зарядов не постоянна (источник отключен). По закону сохранения электрического заряда

q₁+q₂=q'₁+q'₂ (1). Из определения электроемкости конденсатора C=q/U (2), легко получить, что q₁=q₂, так как C₁=C₂ и U₁=U₂ (по условию). Тогда уравнение (1) можно записать в виде 2q=q'₁+q'₂ или 2CU=CU'+C'₂U'. Учитывая, что , получим , e₂=39e₁ или , таким образом .

Ответ: разность потенциалов на обкладках конденсаторов после погружения одного из них в диэлектрик уменьшается и станет равной 15В.

Если конденсаторы не отключать от источника, то напряжение на батарее не изменится и останется равным напряжению источника, т.е. 300В. Заряд же в этом случае не сохраняется, у конденсатора, погружаемого в диэлектрик, он увеличивается пропорционально возрастанию емкости.

Пример 3 на принцип суперпозиции

Определить напряженность и потенциал в точке А электрического поля, созданного двумя точечными зарядами равными 6 нКл каждый, точка А делит пополам расстояние между зарядами.

Решение. Для двух положительных зарядов рисунок имеет вид:

Электрическое поле в точке А создается двумя точечными зарядами. Согласно принципу суперпозиции электрических полей напряженность поля в точке А равна геометрической сумме напряженностей полей, созданных в этой точке зарядами q₁ и q₂ соответственно:

; проецируя на ось X получим: где , .

Если учесть, что и , получим , следовательно, .

, так как . Таким образом, . Потенциал поля в отличие от напряженности является скалярной величиной. Потенциалы складываются алгебраически:

, где и .

Из условия задачи следует, что и . Учитывая, что , получим .

Для положительных зарядов .

Если оба заряда q₁ и q₂ отрицательны 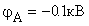и .

Ответ: для одноименных зарядов напряженность электрического поля в точке А равна нулю, а потенциал .

В случае разноименных точечных зарядов рисунок имеет вид:

; . (Докажите самостоятельно).

Пример 4 на движение точечного заряда в электрическом поле с применением закона сохранения энергии или теоремы о кинетической энергии.

Какой минимальной кинетической энергий должен обладать протон, чтобы приблизиться к неподвижному протону на расстояние r₂=10нм, если r₁=10нм?

Первый способ.

Рассмотрим замкнутую систему из двух протонов, так как сила тяжести мала по сравнению с кулоновской силой взаимодействия. В системе отсутствуют силы трения, поэтому сумма потенциальной и кинетической энергий останется постоянной. Таким образом, в силу закона сохранения механической энергии имеем в нашем случае равенство: ,

где E_K1 - начальная кинетическая энергия протона B (начальная величина); E_p1 - потенциальная энергия взаимодействия протонов в начальном состоянии; E_k2 = 0, так как, если E_k1 минимальна, то протон B останавливается, приблизившись на расстояние r₂ к неподвижному протону A.

E_k1 = E_p1 - E_p2, где

E_p1 = q_B j₁, E_p2 = q_B j₂, по определению потенциала.

Потенциал поля точечного заряда q_A на расстоянии r равен

По условию задачи r₁ >> r₂, поэтому начальная потенциальная энергия E_p1 пренебрежимо мала по сравнению с E_p2. Тогда E_k1 = E_p2, или .

Второй способ. Применим для решения задачи теорему о кинетической энергии: работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела .

Пренебрегая силой тяжести протона В и силой гравитационного взаимодействия протонов ввиду малости этих сил по сравнению с кулоновской силой, запишем теорему о кинетической энергии в следующем виде:

, или , так как по определению разности потенциалов и по условию.

Таким образом, получаем тот же результат:

или ;

Проверим реш

⇐ Предыдущая36373839404142434445Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: