 |
Принцип построения производных единиц СИ
|
|
|
|
Международная система единиц физических величин
В1948 г. на IX Генеральной конференции по мерам и весам поступили предложения принять единую систему единиц для всех стран Мира.
В 1954 г. X Генеральная конференция по мерам и весам установила шесть основных единиц (метр, килограмм, секунда, ампер, кельвин, кандела).
Возможность устранения многообразия применяемых единиц появилась после разработки Единой универсальной системы единиц, охватывающей все отрасли науки и техники. Эта система единиц была принята XI Генеральной конференцией по мерам и весам в 1960 г. и получила наименование – “Международная система единиц” – СИ (SI от франц. – Система интернациональная).
В 1963 г. в СССР был введен ГОСТ 9867-61 “Международная система единиц”. С 1982 г. введен ГОСТ 8.417-81 “Единицы физических величин”.
В 1971 г. XIV Генеральная конференция приняла седьмую основную единицу СИ – единицу количества вещества – моль, и к семи основным были добавлены две дополнительные единицы: единица плоского угла – радиан и единица телесного угла – стерадиан.
С 01.09.2003 введен в действие ГОСТ 8.417-2002 “Единицы величин”, в котором установлены единицы физических величин: наименования, обозначения, определения и правила применения этих единиц.
Важнейшие достоинства Международной системы единиц
Наибольшее распространение во всем мире получила Международная система единиц. Основными достоинствами этой системы являются:
1. Универсальность – охват всех областей науки, техники и народного хозяйства.
2. Унификация единиц для всех видов измерений; так, вместо ряда единиц давления, например, атмосферы, миллиметры ртутного столба, миллиметры водяного столба в СИ применяется единая единица давления – паскаль, вместо ряда единиц работы и энергии – одна единица для измерения работы и всех видов энергии (в том числе и теплоты) – джоуль.
|
|
|
3. Применение удобных для практики основных и большинства производных единиц (например, площади – метр квадратный, объема – метр кубический, электрического напряжения – вольт и др.).
4. Когерентность (связность, согласованность) системы; коэффициенты пропорциональности в физических уравнениях, определяющих единицы производных величин, равны безразмерной единице.
5. Четкое разграничение в СИ единицы массы (килограмм) и силы (ньютон).
6. Лучшее взаимопонимание при дальнейшем развитии научно-технических и экономических связей между различными странами.
Международная система единиц является предпочтительной во всех областях науки, техники, торговли, преподавания. В этой системе единицы основных величин выражаются через обозначения этих величин. Применяемые в России единицы представлены в ГОСТ 8.417 – 2002. В нем указаны единицы, подлежащие обязательному применению, допускаемые к применению наравне с обязательными и временно допускаемые к применению.
Образовательный процесс по дисциплине “Метрология, стандартизация и сертификация” построен на применении единиц физических величин в соответствии с таблицами 1, 2, таблицами приложений А.1, Б.1.
Международные обозначения единиц используют: при договорно-правовых отношениях в области сотрудничества с зарубежными странами; при указании единиц величин на табличках, шкалах и щитках средств измерений.
Международные, либо русские обозначения единиц, но одинаковые во всей работе, используют: в нормативных, конструкторских, технологических и других технических документах; учебных пособиях и методических указаниях.
Основные единицы СИ и их определения
Основными единицами, представленными в таблице 1, являются следующие семь единиц: длины – метр (м), массы – килограмм (кг), времени – секунда (с), силы электрического тока – ампер (А), термодинамической температуры – кельвин (К), силы света – кандела (кд), количества вещества (моль).
|
|
|
Таблица 1
Основные единицы СИ
| Величина | Единица | |||
| Наименование | Размерность | Наименование | Обозначение | |
| Русское | Международное | |||
| Длина | L | метр | м | m |
| Масса | M | килограмм | кг | kg |
| Время | T | секунда | с | s |
| Сила электрического тока | I | ампер | А | А |
| Термодинамическая температура | Q | кельвин | К | К |
| Сила света | N | кандела | кд | cd |
| Количество вещества | J | моль | моль | mol |
Первые три единицы (метр, килограмм, секунда) позволяют образовать производные единицы для измерения механических и акустических единиц. При добавлении к ним четвертой единицы (кельвин) можно образовать производные единицы для измерения тепловых величин.
Метр, килограмм, секунда, ампер служат основой для образования производных единиц в области электрических, магнитных измерений, а моль используется для образования единиц в области физико-химических измерений.
Основные единицы в соответствии с решениями Генеральной конференции по мерам и весам имеют следующие определения:
- метр – длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 s;
- килограмм – это единица массы, равная массе международного прототипа килограмма;
- секунда есть время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133;
- ампер это сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным на расстоянии 1 m один от другого в вакууме, вызвал бы на каждом участке проводника длиной 1 m силу взаимодействия, равную 2 · 10–7 N;
- кельвин есть единица термодинамической температуры, равен 1/273,16 части термодинамической температуры тройной точки воды;
- моль – количество вещества системы, содержащей столько же структурных элементов (молекул, атомов, частиц), сколько содержится атомов в углероде-12 массой 0,012 кг.
- кандела это сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 Hz, энергетическая сила света которого в этом направлении составляет 1/683 W/sr;
|
|
|
Принцип построения производных единиц СИ
Производные единицы Международной системы образуются на основании законов, устанавливающих связь между физическими величинами, или на основании определений физических величин (например, площадь – метр квадратный, объем – метр кубический, частота – герц приведены в таблице 2).
Соответствующие производные единицы СИ выводятся из уравнений связи между величинами, выражающими данный физический закон или определение, в случае если другие величины выражаются в единицах СИ. Зависимость каждой производной величины от основных отображается ее размерностью.
Размерность величины представляет собой произведение обозначений основных величин, возведенных в соответствующие степени, и является ее качественной оценкой. Пусть какая-то физическая величина Q выражается через основные величины: длину, массу и время. Размерности основных величин выражаются через обозначения этих величин, т. е. размерности длины, массы и времени записываются dim(l) = L, dim(m) = M, dim(t) = T. В этом случае размерность (dimension) величины dim(Q) выражается формулой размерности:
dim(Q) = [Lα ·Mβ ·Tγ], (1.3)
где L, М, Т – основные величины; α, β,γ – показатели размерности, представляющие собой целые или дробные, положительные или отрицательные целые числа.
Таблица 2
Примеры производных единиц СИ, наименования и обозначения которых
образованы с использованием наименований и обозначений
основных единиц СИ
| Величина | Единица | |||
| Наименование | Размерность | Наименование | Обозначение | |
| Русское | Международное | |||
| Площадь | L2 | квадратный метр | м2 | m2 |
| Объем, вместимость | L3 | кубический метр | м3 | m3 |
| Скорость | LT–1 | метр в секунду | м/с | m/s |
| Ускорение | LT–2 | метр на секунду в квадрате | м/с2 | m/s2 |
| Волновое число | L–1 | метр в минус первой степени | м–1 | m–1 |
| Плотность | L–3M | килограмм на кубический метр | кг/м3 | kg/m3 |
| Удельный объем | L–3M–1 | кубический метр на килограмм | м3/кг | m3/kg |
| Плотность электрического тока | L–2I | ампер на квадратный метр | A/м2 | A/m2 |
| Напряженность магнитного поля | L–1I | ампер на метр | A/м | A/m |
| Молярная концентрация компонента | L–3N | моль на кубический метр | моль/м3 | mol/m3 |
| Яркость | L–2J | кандела на квадратный метр | кд/м | cd/m2 |
|
|
|
Рассмотрим пример использования размерностей.
Пусть требуется определить силу R, действующую на тело в потоке жидкости. Допустим, что движение жидкости настолько медленно, что инерционными силами по сравнению с силами вязкости можно пренебречь.
В этом случае сила R должна зависеть от скорости u, линейного размера тела l и динамической вязкости m. Эта формула в соответствии с формулой (1.3) должна иметь вид
dim{R} = dim(laubmg) = {dim(l) }a {dim(u)}b {dim(m)}g,
но dim(R) = LMT–2; dim(l) = L; dim(u) = LT –1; dim(m) = L –1 MT –1,
поэтому LMT–2 = L a (LT –1) b (L –1 MT –1) g =L a+b –g M g T– b –g.
Для определения показателей a; b и g имеем систему уравнений

откуда получаем a = 1; b = 1 и g = 1 и, следовательно,

где  – безразмерный размер, называемый числом Рейнольдса.
– безразмерный размер, называемый числом Рейнольдса.
Важным принципом, который соблюден в Международной системе единиц, является ее когерентность (согласованность). Так, выбор основных единиц системы обеспечил полную согласованность механических и электрических единиц. Например, ватт (равный джоулю в секунду) – единица механической мощности равняется мощности, выделяемой электрическим током силой 1 ампер при напряжении 1 вольт.
В Международной системе единиц коэффициенты пропорциональности в физических уравнениях, определяющих производные единицы, равны безразмерной величине.
Когерентные производные единицы Международной системы образуются с помощью уравнений связи между величинами, в которых величины приняты равными единице СИ. При этом руководствуются следующими правилами:
1) пишут уравнение, выражающее в явном виде величину; единицу этой величины требуется установить через другие величины, единицы которых являются основными или уже выражены через основные;
2) если в уравнении связи содержится числовой коэффициент, отличный от единицы, то в правую часть подставляют обозначения величин со значениями в единицах СИ, дающими после умножения на коэффициент общее числовое значение, равное 1;
3) величины в правой части уравнения заменяют единицами измерения и выражают их через основные единицы.
Для пояснения способа образования когерентных производных единиц приведем пример. Для образования единицы энергии используется уравнение
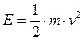 ,
,
где Е – кинетическая энергия; m – масса материальной точки; v – скорость движения материальной точки.
|
|
|
Для образования когерентной производной единицы энергии СИ используют уравнения
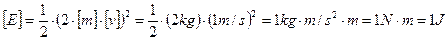
или
 .
.
Таким образом, единицей энергии СИ является джоуль, равный ньютон-метру.
Производные единицы могут иметь специальные наименования и обозначения. Имеют место случаи, когда для выражения производных единиц СИ применяются собственные наименования (прил. А). Эти единицы могут быть использованы для образования других производных единиц СИ (прил. Б).
В приложение А включены единица плоского угла – радиан и единица телесного угла – стерадиан. Единица плоского угла – радиан (рад) – угол между радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении 1 рад = 57 ° 17 ' 44,8 ''. За единицу телесного угла принимается стерадиан (ср) – телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы. Телесный угол Ω измеряют косвенно – путем измерения плоского угла α при вершине конуса с последующим вычислением по формуле
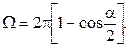
Телесному углу в 1 ср соответствует плоский угол, равный 65˚32', углу π ср – плоский угол 120˚, углу 2π ср – плоский угол 180˚. Для измерения углов применяют угловые градусы, минуты и секунды. Приборов для измерения углов в радианах нет. Единицы плоского и телесного углов используются для образования производных единиц, например угловой скорости и углового ускорения.
В Международную систему единиц при ее принятии в 1960 г. на XI Генеральной конференции по мерам и весам входило три класса единиц: основные, производные и дополнительные (радиан и стерадиан). Единицы радиан и стерадиан классифицировались как дополнительные, однако оставался открытым вопрос о том, являются они основными единицами или производными. В целях устранения двусмысленного положения этих единиц Международный комитет мер и весов в 1980 г. решил интерпретировать класс дополнительных единиц СИ как класс безразмерных производных единиц, для которых Генеральная конференция по мерам и весам оставляет открытой возможность применения или неприменения их в выражениях для производных единиц СИ. В 1995 г. XX Генеральная конференция по мерам и весам постановила исключить класс дополнительных единиц в СИ, а радиан и стерадиан считать безразмерными производными единицами СИ, имеющими специальные наименования и обозначения и которые могут быть использованы или не использованы в выражениях для других производных единиц СИ.
|
|
|


