Физические типы кристаллических решеток

В зависимости от природы частиц, помещающихся в узлах кри­сталлической решетки, и от характера сил взаимодействия между частицами различают четыре типа кристаллических решеток и со­ответственно четыре типа кристаллов: ионные, атомные, металли­ческие и молекулярные.

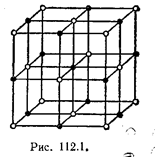
I. Ионные кристаллы. В узлах кристаллической ре­шетки помещаются ионы разных знаков. Силы взаимодействия

Рис. 1.

между ними являются в основном элект­ростатическими (кулоновскими).

Типичным примером ионной решетки может служить изображенная на рис. 1 решетка каменной соли NаС1. Эта решетка принадлежит к кубической системе. Белыми кружками изображе­ны несущие положительный заряд ио­ны натрия, черными кружками — отрицательные ионы хлора. Как видно из рисунка, ближайшими соседями иона данного знака будут ионы противоположного знака. В газообразном состоянии NaCl состоит из молекул, в которых объединяются попарно ионы натрия с ионами хлора. Образующая молекулу группировка из иона Na и иона С1 утрачивает в кристалле обособленное существование.

Ионный кристалл состоит не из моле­кул, а из ионов.

2. А т о м н ы е к р и с т а л л ы. В узлах кристаллической ре­шетки помещаются нейтральные атомы.

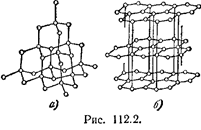
Типичными примерами атомных кристаллов могут служить алмаз и графит. Оба эти вещества тождественны по химической природе (они построены из атомов углерода), но отличаются кри­сталлическим строением. На рис. 2, а показана решетка алмаза, на рис. 2,6—решётка графита.

Для этой решетки алмаза характерно то, что каждый атом окружен че­тырьмя равноотстоящими от него соседями, расположенными в вершинах правильного тетраэд­ра.

Рис. 2.

3. Металлические кристаллы. Во всех узлах кристаллической решетки расположены положительные ионы ме­талла. Между ними беспорядочно, подобно молекулам газа, дви­жутся электроны, отщепившиеся от атомов при образовании ионов. Эти электроны играют роль «цемента», удерживая вместе положи­тельные ионы; в противном случае решетка распалась бы под дей­ствием сил отталкивания между ионами. Вместе с тем и электроны удерживаются ионами в пределах кристал­лической решетки и не могут ее покинуть.

4. Молекулярные кристаллы. В узлах кристалли­ческой решетки помещаются определенным образом ориентирован­ные молекулы. Силы связи между молекулами в кристалле имеют ту же природу, что и силы притяжения между молекулами, приво­дящие к отклонению газов от идеальности.

Моле­кулярные решетки образуют, например, следующие вещества:

Нг, Na, Оз, СОа, НаО. Таким образом, обычный лед, а также так называемый сухой лед (твердая углекислота) представляют собой молекулярные кристаллы.

Дефекты в кристаллах

Дефектами кристаллов называют нарушения идеальной кристал­лической структуры. Такое нарушение может заключаться в от­сутствии атома в узле решетки (вакансия), в замене атома данного вещества (своего атома) чужим атомом (атомом примеси), во внед­рении лишнего атома (своего или чужого) в межузельное прост­ранство. Подобные дефекты называются точечными. Они вы­зывают нарушения правильности решетки, распространяющиеся на расстояния порядка нескольких периодов.

Кроме точечных, существуют дефекты, сосредоточенные вблизи некоторых линий. Их называют линейными дефектами

Рис. 1.

Рис. 2.

или дислокациями. Дефекты такого вида нарушают правиль­ное чередование кристаллических плоскостей. Простейшими ви­дами дислокации являются краевая и винтовая дисло­кации.

Краевая дислокация обусловливается лишней кристаллической полуплоскостью, вдвинутой между двумя соседними слоями ато­мов (рис. 1). Край этой полуплоскости образует дислокацию данного вида. Линией дислокации является перпендикулярная к плоскости рисунка прямая, отмеченная знаком .

Винтовую дислокацию можно представить как результат разре­за кристалла по полуплоскости и последующего сдвига лежащих по разные стороны разреза частей решетки навстречу друг другу на величину одного периода (рис. 2). Внутренний край разре­за образует винтовую дислокацию (см. пунктирную прямую на рисунке). Кристалл с винтовой дислокацией фактически состоит из одной кристаллической плоскости, которая изогнута по винтовой поверхности (такую поверхность называют геликоидом). Линия дислокации совпадает с осью винта. При каждом обходе вокруг этой линии кристаллическая плоскость смещается на один период.

Рис. 3.

Мы рассмотрели два простейших (предельных) вида дислока­ции. В обоих случаях линии дислокации являются прямыми. В об­щем случае линии дислокации могут быть кривыми.

Дефекты оказывают сильное влияние на физические свойства кристаллов, в том числе и на их прочность. В частности, дисло­кации служат причиной того,

что пластическая деформация (т.е. деформация, сохраняющаяся после снятия напряжения, вызвавшего эту деформацию) реальных кристаллов происходит под воздействием напряжений на несколько порядков меньших, чем вычисленное для идеальных кристаллов.

У монокристаллов металлов легко происходит сдвиг вдоль атомных слоев. Не следует представлять себе этот процесс так, что все атомы слоя смещаются одновременно как одно целое. В дей­ствительности атомы перескакивают в новые положения неболь­шими группами поочередно. Такое поочередное перемещение атомов может быть представлено как движение дислокации. Для пере­мещения дислокации достаточно напряжений, много меньших, чем для перемещения всего атомного слоя сразу. На рис. 3 показаны последовательные стадии процесса, происходящего в кристалле под действием сил, обусловливающих сдвиг. Первоначально имевшаяся дислокация под воздействием созданных в кристалле напряжений перемещается вдоль кристалла. Это перемещение со­провождается поочередным сдвигом атомов слоя, лежащего над дис­локацией, относительно атомов слоя, лежащего под дислокацией.

Перемещению дислокации препятствует наличие других дефектов в кристалле, например, присутствие атомов примеси. Дислокации тормозятся также при пересечении друг с другом. Если коли­чество дислокации и других дефектов в кристалле мало, дислокации перемещаются практически свободно. В результате сопротивление сдвигу будет невелико. Увеличение плотности дислокации и воз­растание концентрации примесей приводит к сильному торможению дислокации и прекращению их движения. В результате; проч­ность материала растет. Так, например, повышение прочности же­леза достигается растворением в нем атомов углерода (такой раст­вор представляет собой сталь).

Пластическая деформация сопровождается разрушением крис­таллической решетки и образованием большого количества дефек­тов, препятствующих перемещению дислокации. Этим объясняется упрочение материалов при их холодной обработке.

Винтовая.дислокация часто возникает в процессе роста кристал­лов из раствора или расплава. Захват атома гладкой плоской кри­сталлической поверхностью энергетически менее выгоден и по­этому менее вероятен, чем присоединение атома к ступеньке, су­ществующей на поверхности кристалла с винтовой дислокацией. Поэтому кристаллы предпочитают расти со встроенной внутрь винтовой дислокацией. Новые атомы присоединяются к краю сту­пеньки, вследствие чего рост кристалла происходит по спирали.

Теплоемкость кристаллов

Расположение частиц в узлах кристаллической решетки отве­чает минимуму их взаимной потенциальной энергии, т.е. частица находится в положении равновесия. При смещении частиц из положения равновесия в любом направлении появляется сила, стремящаяся вернуть частицу в первоначальное положение, вследствие чего возникают колебания частицы. Колебание вдоль произвольного направления можно представить как наложение колебаний вдоль трех взаимно перпендикулярных направлений. Поэтому каждой частице в кристалле следует приписывать три колебательные степени свободы.

Из молекулярно-кинетической теории известно, что на каждую колебательную степень свободы в среднем приходится энергия, равная kT (k – постоянная Больцмана). Следовательно, на каждую частицу—атом в атомной ре­шетке, ион в ионной или металлической решетке — приходится в среднем энергия, равная 3kT.

Ограничившись рассмотрением химически простых веществ, образующих атомные или металлические кристаллы, для внутрен­ней энергии моля вещества в кристаллическом состоянии можно написать выражение

,

где 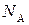- число Авогадро, R – универсальная газовая постоянная.

Приращение внутренней энергии, соответствующее повышению температуры па один кельвин, равно теплоемкости при постоянном объеме. Следовательно,

Поскольку объем твердых тел при нагревании меняется мало, их теплоемкость при постоянном давлении незначительно отличается от теплоемкости при постоянном объеме, так что можно положить и говорить просто о теплоемкости твердого тела.

И, так согласно теплоемкость моля химически простых тел в кристаллическом состоянии одинакова и равна . Это утвер­ждение составляет содержание закона Дюлонга и Пти, установленного опытным путем. Закон выполняется с довольно хорошим приближением для мно­гих веществ при комнатной тем­пературе. Однако, например, ал­маз имеет при комнатной темпе­ратуре теплоемкость, равную всего, примерно 0,7R.

Рис. 1.

Более того, вопреки (1) теплоемкость кристаллов зависит от температуры, причем зависи­мость имеет характер, показан­ный на рис. 1. При достаточно высокой, характерной для каждого вещества температуре начинает выполняться равен­ство (1). У большинства тел это достигается уже при комнатной температуре, у алмаза же теплоемкость достигает значения 3R лишь при температуре порядка 1000°С,

Строгая теория, теплоемкости твердых тел, созданная Эйнштей­ном и Дебаем, учитывает, во-первых, квантование энергии колеба­тельного движения. Во-вторых, теория учитывает, что колебания частиц в кристаллической решетке не являются незави­симыми. Эта теория) находится в хорошем согласии с опытными данными. В частности, для высоких температур она приводит к вы­ражению (1).

 

Эффект Холла

Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и по­ля, возникает разность потенциалов 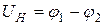(рис. 1). Это явление было обнаружено Холлом в 1879 г. и называется эффек­том Холла или гальваномагнитным явлением.

Холловская разность потенциалов определяется выражением

(1)

Здесь — ширина пластинки, — плотность тока, В — магнит­ная индукция поля, R — коэффициент пропорциональности, полу­чивший название постоянной Холла.

Эффект Холла очень просто объясняется электронной теорией. В отсутствие магнитного поля ток в пластинке обусловливается электрическим полем (рис. 2). Эквипотенциальные, поверхности этого поля. образуют систему перпендикулярных к вектору плоскостей. Две из них изображены на рисунке сплошными прямы­ми линиями. Потенциал во всех точках каждой поверхности, а сле­довательно, и в точках / и 2 одинаков. Носители тока—электроны — имеют отрицательный заряд, поэтому скорость их упорядоченного) движения и направлена противоположно вектору плотности тока .

При включении магнитного поля каждый носитель оказывается под действием магнитной силы F, направленной вдоль стороны Ь пластинки и равной по модулю

(2)

В результате у электронов появляется составляющая скорости, направленная к верхней (на рисунке) грани пластинки. У этой у грани образуется избыток отрицательных, соответственно у нижней грани — избыток положительных зарядов. Следовательно, возникает дополнительное поперечное электрическое поле . Когда напряженность этого поля достигает такого значения, что его действие на заряды будет уравновешивать силу (2), устано­вится стационарное распределение зарядов в поперечном направ­лении. Соответствующее значение определяется условием: 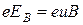. Отсюда

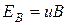
Поле складывается с полем в результирующее поле Е, Эквипотенциальные поверхности перпендикулярны к вектору на­пряженности поля. Следовательно, они повернутся и займут поло­жение, изображенное на рис. 2 пунктиром. Точки / и 2, которые

прежде лежали на одной и той же эквипотенциальной поверх­ности, теперь имеют разные потенциалы. Чтобы найти напряжение, возникающее между этими точками, нужно умножить расстояние между ними на напряженность Ев.

Выразим и через , п и е в соответствии с формулой . В ре­зультате получим

(3)

Последнее выражение совпадает с (1), если положить

(4)

Из (4) следует, что, измерив постоянную Холла, можно найти концентрацию носителей тока в данном металле (т. е. число носителей в единице объема).

Важной характеристикой вещества является подвижность в нем носителей тока. Подвижностью носителей тока называется средняя скорость, приобретаемая носителями при напряженности электрического поля, равной единице. Если в поле напряженности Е носители приобретают скорость и, то подвижность их 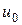равна

(5)

Подвижность можно связать с проводимостью 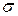и концентрацией носителей п. Для этого разделим соотношение на напряженность поля Е. Приняв во внимание, что отношение к Е дает 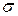, а отношение и к Е— подвижность, получим

(6)

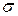Измерив постоянную Холла и проводимость , можно по формулам (4) и (6) найти концентрацию и подвижность но­сителей тока в соответствующем образце.

Эффект Холла наблюдается не только в металлах, но и в полу­проводниках, причем по знаку эффекта можно судить о принадлеж­ности полупроводника к п- или р-типу. На рис. 3 сопоставлен

эффект Холла для образцов с положительными и отрицательными носителями. Направление магнитной силы изменяется на противоположное как при изменении направления движения заряда, так) и при изменении его знака. Следовательно, при одинаковом направлении тока и поля магнитная сила, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней (на рисунке) грани выше, чем нижней, а в случае отрицательных носителей—ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока.

Любопытно, что у некоторых металлов знак соответствует положительным носителям тока. Объяснение этой аномалии дает квантовая теория.

Эффект Мёссбауэра

Атомы особенно интенсивно поглощают свет частоты, соот­ветствующей переходу из основного в ближайшее к нему воз­бужденное состояние. Это явление называется резонансным поглощением. Возвращаясь затем в основное состояние, атомы испускают фотоны резонансной частоты. Соответствую­щее излучение носит название резонансного излучения или резонансной флуоресценции.

Подобно атомам, атомные ядра имеют дискретные уровни энергии, самый низкий из которых называется нормальным, остальные — возбужденными. Переходы между этими уровнями приводят к возникновению коротковолнового электромагнитного излучения, получившего название -лучей.

Соответствующие переходу кванто­вой системы между двумя состояниями линия испускания и ли­ния поглощения смещены друг относительно друга на

где R— энергия отдачи.

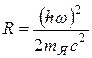
где масса ядра.

Ширину спектральной линии, сдвиг линий и т.п. мы будем выражать в единицах энергии, умножая для этой цели соответствующие частоты на постоянную Планка . В этих единицах сдвиг линий испускания и поглощения будут характеризоваться величиной 2R, а доплеровское уширение линии—величиной

где скорость теплового движения молекул.

На рис. 1 изображена типичная для -фотонов картина, по­казывающая взаимное расположение линий испускания и по­глощения. Ясно, что лишь небольшая часть испускаемых фото­нов (их относительное количество определяется соответствую­щими ординатами линии испускания) может испытать резонанс­ное поглощение, причем вероятность их поглощения мала (эта вероятность определяется ординатами линии поглощения). Поэтому для ядер эффект резонансного поглощения не удавалось наблюдать долгое время.

До 1958 г. резонансное поглощение -лучей удавалось на­блюдать с помощью устройств, в которых источник -излучения двигался со скоростью v по направлению к поглощающему ве­ществу. Это достигалось путем помещения радиоактивного вещества на ободе вращающегося диска (рис. 2). Диск нахо­дился внутри массивной свинцовой защиты, поглощающей -лучи. Пучок излучения выходил наружу через узкий канал

и попадал на поглощающее вещество. Установленный за погло­тителем счетчик -квантов регистрировал интенсивность излу­чения, прошедшего через поглотитель. Вследствие эффекта До­плера частота излучаемых источником -лучей увеличивалась на , где v— скорость источника относительно по­глотителя, т.е. линия испускания смещалась вправо. Подобрав надлежащим образом скорость вращения диска, можно было наблюдать резонансное поглощение.

В 1958 г. Р. Л. Мёссбауэр исследовал ядерное резонансное поглощение -лучей (изотопа иридия с массовым числом 191), линии испус­кания и поглощения отчасти перекрываются, и резонансное по­глощение могло наблюдаться. Чтобы уменьшить поглощение, Мёссбауэр решил охладить источник и поглотитель, рассчиты­вая таким путем уменьшить доплеровскую ширину и, следовательно, перекрывание линий. Однако вместо ожидаемого уменьшения Мёссбауэр обнаружил усиление резонансного поглощения. Результаты опыта указывали на то, что у охлажденного линии испускания и поглощения -лучей совпадают и имеют очень малую ширину, это явление упругого (т. е. не сопровождающегося изменением внутренней энергии тела) ис­пускания или поглощения -квантов было названо эффектом Мёссбауэра.

Физическая суть эффекта Мёссбауэра состоит в том, что при испускании -кванта ядром, находящимся в узле кристал­лической решетки, энергия перехода фотоном может распределяться между - квантом, и колебаниями решетки. В последнем случае наряду с -квантом возникнут фононы. Таким образом, энергия перехода может распределяться между -квантом и фононами. Мёссбауэровский переход осуществляется в том случае, если колеба­тельное состояние решетки не изменяется и -квант получает всю энергию перехода.

Итак, при испускании или поглощении -кванта ядром, на­ходящимся в узле кристаллической решетки, могут происхо­дить два процесса: 1) изменение колебательного состояния ре­шетки т.е. часть энергии перехода при испускании -кванта идет на образование фононов 2) передача импульса -кванта решетке как целому, без изменения ее колебательного состояния, т. е. упругое испускание и поглощение -кванта. Каждый из этих процессов обладает определенной вероят­ностью, значение которой зависит от конкретных свойств кри­сталла, энергии -кванта и температуры. С понижением тем­пературы относительная вероятность упругих процессов воз­растает.

На рис. 3. Показаны типичные спектры испускания и поглощения -квантов (Е-энергия -квантов, I-интенсивность, R-средняя энергия отдачи). Оба спектра содержат практически совпадающие очень узкие линии, отвечающие упругим процессам. Эти линии располагаются на фоне широких смещенных линий, обусловленных процессами, сопровож-дающимися изменением колебательного состояния решетки. С понижением температуры фон ослабляется, а доля упругих процессов воз­растает, но никогда не достигает единицы.

Эффект Мёссбауэра нашел многочисленные применения. В ядерной физике он используется для нахождения времени жизни возбужденных состояний ядер (через Г), а также для определения спина, магнитного момента и электрического квадрупольного момента ядер. В физике твердого тела эффект Мёссбауэра применяется для изучения динамики кристаллической решетки и для исследования внутренних электрических и магнитных полей в кристаллах.

Благодаря крайне малой ширине мёссбауэровских линий метод движущегося источника позволяет осуществить измере­ние энергии -квантов с огромной относительной точностью (до 15-й значащей цифры). Этим обстоятельством воспользовались американские физики Паунд и Ребка для обнаружения предсказанного общей теорией относительности гравитационного красного смещения частоты фотонов). Из общей теории относительности следует, что часто­та фотона должна изменяться с измене­нием гравитационного потенциала. Это обу­словлено тем, что фотон ведет себя подобно частице, обладающей гравитационной мас­сой, равной (см. параграф 71 1-го тома). Поэтому при прохождении в однородном гравитационном поле, характе­ризуемом напряженностью g, пути 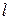в на­правлении, противоположном направлению силы , энергия фотона должна умень­шиться на . Следовательно, энергия фотона ста-. нет равной

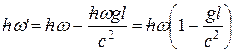
Отсюда

где изменение гравитационного потенциала. Полученная нами формула справедлива и для фотона, движущегося в неод­нородном гравитационном поле (в этом случае ).

Свет, приходящий на Землю от звезд, преодолевает сильное притягивающее поле этих светил. Вблизи же Земли он испы­тывает действие лишь очень слабого ускоряющего поля. По­этому все спектральные линии звезд должны быть немного сме­щены в сторону красного конца спектра. Такое смещение, назы­ваемое гравитационным красным смещением, было качественно подтверждено астрономическими наблюдениями.

Паунд и Ребка предприняли попытку обнаружить это явле­ние в земных условиях. Они расположили источник -излучения () и поглотитель в высокой башне на расстоянии 21 м друг от друга (рис. 4). Относительное изменение энергии -фотона при прохождении этого расстояния составляет всего

Это изменение обусловливает относительное смещение линий поглощения и испускания и должно проявиться в небольшом ослаблении резонансного поглощения. Несмотря на крайнюю малость эффекта (сдвиг составлял около ширины линии), Паунду и Ребке удалось обнаружить и измерить его с доста­точной степенью точности. Полученный ими результат составил 0,99 ± 0,05 от предсказанного теорией. Таким образом, удалось убедительно доказать наличие гравитационного смещения час­тоты фотонов в условиях земной лаборатории.

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: