Зернистых материалов и жидкости

В зависимости от принципа действия пневмотранспортной установки (ПУ) СА устанавливается в начале, в конце, а в некоторых случаях и в середине пневмотрассы [14, 25, 30]. В установках нагнетательного действия возможны различные варианты применения эжектора (см. рис. 5.1).

Так, например, СА, изображенные на рис. 4.4 а и 4.14 б представляют собой устройства, обеспечивающие необходимые параметры пневмотранспортного потока а именно, — давление и расход газа. Причем в обоих случаях возможен подсос атмосферного воздуха. Из рис. 4.4 б следует, что применение эжектора с кольцевым соплом весьма актуально в ПУ всасывающе-нагнетательного действия, причем крупность материала не имеет принципиального значения. На рис. 4.4 в СА играет роль тягового эжектора. В этом качестве СА широко используется при разработке различных пневмонасосов [25], а также при проектировании всасывающих сопел (см. п. 2 и рис. 3.2).

Рис. 4.4. Применение СА для пневмотранспорта зернистых материалов (а, б, в, г) и жидкости (д): а) в ПУ нагнетательного действия; б) в ПУ всасывающе-нагнетательного действия; в), г), д) в качестве тягового эжектора, питателя и струйного однофазного насоса соответственно; 1— СА с центральным соплом; 2 — загрузочное устройство; 3 — СА с кольцевым соплом; 4 — фильтр; 5 — промежуточная емкость; 6 — шахта; 7 — задвижка; 8 — транспортный трубопровод; 9 — обратный клапан; 10 — противовес; 11 — сопло; 12 — пористое днище; 13 — всасывающий трубопровод; 14 — колодец

СА, изображенные на рис. 5.1, а и 5.1, б, следует отнести к аппаратам с большой степенью расширения () и достаточно высокой степенью сжатия (), т. е. рабочая и инжектируемая среды являются упругими. В СА, изображенных на рис. 4.4 г и 4.4 д, в качестве рабочей среды также используется упругая среда — газ, а инжектируемой средой является неупругая среда — сыпучее твердое тело или жидкость. Степень расширения рабочего потока может быть как сверхкритической (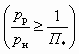), так и докритической ( и одновременно ). Степень сжатия, напротив, мала (), т. к. инжектируемая среда представляет собой смесь сыпучего твердого материала и газа (чаще воздуха) или жидкости.

СА на рис. 4.4 г представляет собой питатель, в который материал, подлежащий транспортировке, подается непосредственно в приемную камеру, а далее увлекается струей воздуха, выходящей с большой скоростью из рабочего сопла. Общее сопротивление ПУ не должно превышать (0,2…0,4) · 10⁵ Па.

СА, принципиальная схема которого представлена на рис. 4.4 д, применяется для перекачки жидкости из резервуаров и колодцев и других целей.

Поскольку уравнения, характеризующие состояние упругой (1) и неупругой (2) сред, имеют вид

и 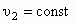, (4.3)

то, очевидно, условию неупругости (несжимаемости) соответствует показатель адиабаты k.

При расчете любого СА широко используются газодинамические функции, связывающие термодинамические параметры потока (температуру, давление, плотность и др.) с его приведенной скоростью l, представляющей собой отношение скорости газа при его адиабатном течении w к критической скорости а _*: т. е.

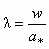. (4.4)

Поскольку для упругой среды

, (4.5)

, (4.6)

то

. (4.7)

может изменяться от 0 до при Т = 0, т. е. при истечении потока в абсолютный вакуум.

В свою очередь, для условно несжимаемой среды будем иметь

, (4.8)

, (4.9)

. (4.10)

По смыслу выражения (4.9) критическая скорость неупругой среды равна скорости истечения этой среды в абсолютный вакуум, когда внешнее давление р = 0.

Наиболее часто используются следующие функции:

- функция П (l) — относительное давление, т. е. отношение давления р адиабатно движущегося газа в данном сечении к давлению торможения р _о;

- функция e(l) — относительная плотность, т. е. отношение плотности ρ адиабатно движущегося потока в данном сечении к его плотности ρ_о в заторможенном состоянии;

- функция q (l) — относительная массовая скорость, т. е. отношение массовой скорости r w адиабатно движущегося потока в данном сечении к массовой скорости этого потока r_* а _* в критическом сечении, определяемая как

. (4.11)

Взаимосвязь основных газодинамических функций для упругой и неупругой сред приведена в табл. 4.1.

Исходные данные для расчета:

- G _н (G _р или G _с) — расход газа в инжектируемом (рабочем или смешанном) потоке, кг/с или u;

- p _p p _н (p _н или р _с) — статические давления рабочего, (инжектируемого или (смешанного) потоков, Па;

- T _p, T _н — температуры рабочего и инжектируемого потоков, К;

- r_р (r_н (или r_с) — плотности рабочего, (инжектируемого (или смешанного) потоков, кг/м³;

- k _p = k _н = k — показатель адиабаты;

- R _р = R _н = R — удельная газовая постоянная, Дж/(кг·К);

Основные задачи расчета СА:

1. Определение максимально достижимого коэффициента инжекции или максимально достижимого давления сжатия при заданных параметрах рабочего (от компрессора) (р _р, Т _р) и инжектируемого (р _н, Т _н) потоков перед СА и заданном либо давлении сжатия р _с, либо коэффициенте инжекции u;

2. Определение геометрических размеров СА;

3. Расчет поля рабочих характеристик СА.

Решение первой задачи существенно зависит от степени расширения и сжатия, что связано с возникновением так называемого предельного режима работы. В наибольшей мере это относится к СА с большой степенью расширения 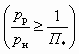и умеренной степенью сжатия . К таким аппаратам относятся, согласно [5], газо (паро)-струйные компрессоры.

 

Таблица 4.1

Взаимосвязь основных газодинамических функций для упругой

и неупругой сред

Функция	Основные соотношения	Значения газодинамических функций
l = 0	l =1,0	l = lmax
λ	λ
	λ
П		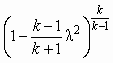П	1,0
		П	1,0
ε		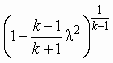	1,0
			1,0		1,0
q
	λ				1,0

Решение первой задачи существенно зависит от степени расширения и сжатия, что связано с возникновением так называемого предельного режима работы. В наибольшей мере это относится к СА с большой степенью расширения 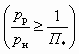и умеренной степенью сжатия . К таким аппаратам относятся, согласно [5], газо- и пароструйные компрессоры.

4.4. Расчет СА с большой степенью расширения (р_р / р_н ³ > 1/П_*)

и умеренной степенью сжатия (21,52 > р_с / р_н > 12,25).

Критические скорости рабочего и инжектируемого потоков a_р* и a_н*, равные местной скорости звука, находят из выражения (4.6). Далее по величине относительного давления П _рн = р _н / р _р, воспользовавшись соотношениями, приведенными в табл. 4.1, находят параметры рабочего потока на входе в камеру смешения — l_рн и q _рн.

Поскольку максимально достигаемый коэффициент инжекции u зависит от параметров потоков в сечениях 2–2 и 3–3 камеры смешения (см. рис. 4.3), то решение задачи, связанной с его определением, возможно лишь методом перебора целого ряда значений l_с3 в выходном сечении 3–3 камеры смешения (см. рис. 4.3). Интервал возможных значений l_с3 ограничивается рядом условий, приведенных ниже.

Прежде всего, этот интервал находится в области l_с3 < 1, т. к. скорость смешанного потока не может быть больше критической. Скорость инжектируемого потока должна соответствовать аналогичному требованию в любом сечении s –s цилиндрической камеры смешения, т. е. l_нs = 1. Поэтому реальный интерес имеют лишь те значения l_с3, при которых это условие выполняется. Если l_нs = 1 и q _нs = 1, то в аппарате как уже отмечалось выше, возникает второй предельный режим, характеризующийся максимально возможным коэффициентом инжекции:

, (4.10)

где . В этом случае

, (4.11)

а величина q _c3 должна отвечать условию

. (4.12)

В противном случае работа СА невозможна. Параметры рабочего потока в этом сечении (l_рs и q _рs) находят также по величине относительного давления П _ps, для которой с учетом (5.11) можно записать

, (4.13)

где П _н* = П _*.

Расчет достижимого коэффициента инжекции для ряда значений l_с3 осуществляется методом последовательных приближений по следующей схеме.

Задаваемая величина l_с3 однозначно определяет остальные газодинамические функции П _с3 и q _с3, характеризующие смешанный поток (см. табл. 4.1). Невыполнение условия (5.12) означает переход к следующему более низкому значению l _с3. В противном случае находят (u _пр)₂, воспользовавшись формулой (4.3., 4.10). Этот параметр определяет взаимосвязь между газодинамическими функциями смешанного потока в сечении 3 – 3 (см. рис. 4.3) и аналогичными функциями инжектируемого потока в некотором сечении s – s, где l_нs = 1 и q _нs = 1. Принимая эту величину в качестве предварительного значения u ' = (u _пр)₂, можно найти приведенную массовую скорость q _н2 инжектируемого потока на входе в камеру смешения из выражения

. (4.14)

Воспользовавшись зависимостью q (l) (см. табл. 4.1), можно записать

. (4.15)

Разрешая уравнение (4.15) любым численным методом, следует иметь в виду неравенство l_н2 < 1, т. к. q неоднозначным образом определяет l. Зная l_н2, нетрудно найти П _н2. Далее, воспользовавшись методом итераций, находят уточненное значение u. При этом расчеты проводятся в следующей последовательности:

; (4.16)

; (4.17)

; (4.18)

, (4.19)

где k ₁ = j₁j₂j₃; k ₂ = j₂j₃j₄. В свою очередь j₁; j₂; j₃; j₄ — эмпирические коэффициенты, численные значения которых рекомендуется принимать соответственно 0,95; 0,975; 0,9 и 0,925. При этом k ₁ = 0,834; k ₂ = 0,812.

Если полученное значение u < (u _пр)₂, то окончательно принимают u = (u _пр)₂. Если u > (u _пр)₂, то задаются u ' = u и по формулам (4.14)–(4.19) продолжают вычисления до тех пор, пока не будет достигнуто | u ' – u | < 10^–3.

Аналогичные расчеты проводятся и для других значений λ_с3. Затем из полученных данных осуществляется выбор оптимальных параметров l_н2, q _н2, l_с3 и q _с3, при которых u = u _max.

Таким же образом решается задача по определению достижимой степени сжатия в случае, когда задан коэффициент инжекции u, только вместо (u _пр)₂ находят :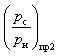

, (4.20)

где

. (4.21)

Величина определяется соотношением:

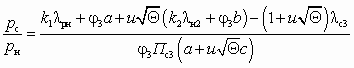, (4.22)

где a = , b = , c = .

Принимая предварительно искомое значение (р _с / р _н)′ = (р _с / р _н)_пр2, находят q _н2 по (4.14), а затем аналогично предыдущему l_н2 и, наконец, П_н2. Уточненное значение р _с/р_н определяется из выражения (4.22).

Если полученное по (4.22) значение р _с / р _н > (р_с / р_н)_пр2, то принимают р _с / р _н = (р _с / р _н)_пр2. В противном случае задаются (р _с / р _н)′ = р _с / р_н и продолжают вычисления по приведенному алгоритму до тех пор, пока не будет достигнуто |(р _с / р _н)′ – р_с / р _н | < 10^–3.

Полученная информация является основой для расчета геометрических размеров СА.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: