Формирование передаточной функции

Учитывая, что ARC-фильтры обычно строятся из каскадно-соединенных звеньев второго порядка, целесообразно передаточную функцию таких фильтров формировать из произведения сомножителей тоже второго порядка. Они имеют вид:

.

Тогда вся передаточная функция рассчитываемого фильтра будет:

. (7.1)

Коэффициенты в числителе могут иметь одинаковую величину и рас­считываться по формуле:

.

­Коэффициенты в знаменателе (7.1) находятся по формулам:

; и ; (7.2)

где - значение полюсов (6.1).

;

;

;

;

;

.

Значения всех рассчитанных коэффициентов сведем в таблицу 3.

Таблица 3

Номер сомножителя	Значение коэффициентов
ai1	bi1	bi0
	150910.84	71478.946	3.805×1011
	150910.84	41915.37	5.394×1011
	150910.84	29563.576	2.683×1011

Подставляя найденные коэффициенты в H(p) (7.1) получим: (7.3)

8. Расчет элементов схемы фильтра

В качестве типовой выбираем простейшую схему ПФ на одном опе­рационном усилителе (ОУ) (рис. 8.1).

Рисунок 8.1 ПФ на одном опе­рационном усилителе

Если составить эквивалентную схе­му, заменив ОУ ИНУНом, то, используя любой из методов анализа цепей, можно получить передаточную функцию, описывающую работу схе­мы на рис. 8.1, в виде:

(8.1)

Из формулы (8.1) видно, что рассмотренная схема является схемой второго по­рядка. Следовательно, для реализации функции H(p) (7.3) потребуется три по­добных схемы или три звена, соединенных каскадно. Расчет элементов этих схем R₁, R₂, С₃, С₄, R₅ ведется путем сравнения идентичных коэффи­циентов в двух последних формулах (7.3) и (8.1).

(8.2)

Для первого звена ПФ берутся коэффициенты из первого сомножите­ля первой формулы (7.3):

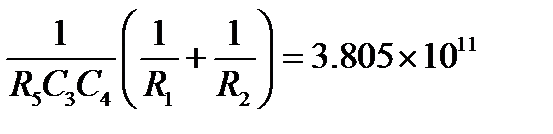
В системе (8.2) пять неизвестных и только три уравнения. Система не решаема. Поэтому зададимся значениями, например, ем­костей конденсаторов С₃ и C₄ (в ходе настройки фильтра при его изготов­лении принято использовать переменные сопротивления, т. к. переменных конденсаторов с большой емкостью не существует).

Если принять С₃ = С₄ = 2 нФ, то решая (8.2) систему, получим:

R₁ = 3.313 кОм, R₅ = 13.99 кОм, R₂ = 47.645Ом.

Составляя аналогичную систему для второго звена при тех же

С₃= С₄= 2 нФ, получим:

R₁ = 3.313 кОм, R₅ = 23.858 кОм, R₂ = 19.541 Ом.

Аналогично для третьего звена:

R₁ = 3.313 кОм, R₅ = 33.825 кОм, R₂ = 27.774 Ом

Рассчитанные сопротивления не соответствуют стандартным номина­лам резисторов. Поэтому для сопротивлений R₁и R₅в каждом звене бе­рутся резисторы с номиналом, ближайшим к рассчитанному значению. Сопротивление R₂ берется составным, из последовательно соединенных постоянного и переменного резисторов, что позволит осуществлять общую настройку фильтра.

 

Проверка результатов расчета

Известно, что H(p) всего фильтра будет:

H(p)=H₁(p)H₂(p)H₃(p), (9.1)

где значения каждого сомножителя будут отличаться из-за разницы в зна­чениях сопротивлений звеньев фильтра.

Произведем замену переменной вида p = j ω в (8.1), в результате чего получаем выражение:

Находим модуль H(j ω ) в виде:

(9.2)

Зная H( ω ), легко найти зависимость ослабления от частоты вначале каждого

звена, а затем всего фильтра:

A(ω)=A₁(ω)+A₂(ω)+A₃(ω), (9.3)

где: 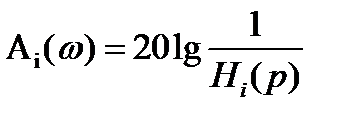. (9.4)

Выполним расчет звеньев фильтра. Из предыдущего раздела (8) берем значения элементов С ₁, С ₂, R₁, R₅.

Подставляем эти значения в (9.2):

Все результаты сво­дим в таблицу 4.

Таблица 4

f, кГц	f з1	fп1	f0	fп2	fз2
74.954	80.952	98.168	119.048	128.572
H1(ω)	0.438	0.604	2.111	0.604	0.438
H2(ω)	0.223	0.273	0.578	3.031	1.032
H3(ω)	1.463	4.299	0.82	0.387	0.317
H(ω)	0.143	0.708	1.019	0.655	0.143
A1(ω)	7.166	4.377	-6.491	4.377	7.166
A2(ω)	13.02	11.286	4.761	-9.632	-0.272
A3(ω)	-3.304	-12.667	1.566	8.255	9.988
A(ω)	16.882	2.996	-0.164	3.669	16.882

Из расчета ясно, что значение H( ω ) (9.2) наиболее сильно зависит от величины сопротивления R₂, поэтому именно это сопротивление необходимо выбирать переменным.

На рис. 9.1 приведена ожидаемая теоретическая кривая зависимости ослабления фильтра от частоты. На рис. 9.2 приведена принципиальная схема активного полосового фильтра.

Рисунок 9.1 Зависимости ослабления фильтра от частоты

 

 

Рисунок 9.2 Принципиальная схема активного полосового фильтра.

R ₁, R ₂, R ₅ – сопротивление 1-го звена

R′ ₁, R′ ₂, R′ ₅ – сопротивление 2-го звена

R″ ₁, R″ ₂, R″ ₅ – сопротивление 3-го звена

 

Литература

1. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. «Основы теории цепей».

Учебник-М.: Радио и связь, 2000 г.

2. Бакалов В.П., Воробиенко П.П., Крук Б.И. «Теория электрических цепей».

Учебник - М.: Радио и связь, 1998 г.

3. Бакалов В.П., Рожков В.М., Сметанина М.И., Методические указания

«Расчет электрических фильтров». Новосибирск, 2002 г.

4. Зааль Р. Справочник по расчету фильтров. - М.: Радио и связь, 1983 г.

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: