Расчет предварительных типовых задач, входящих в состав ВЭР1, ВЭР2 и ВЭР3

5.2.1. Расчет координат линии огрганичения предельной пропускной способности ГЭС - Q_ГЭС^пред в зависимости от Z_вб.

Расчет приведен в табл.5.3 по следующему алгоритму. Задаемся рядом значений Н_а в диапазоне от Н_а^min до Н_а^max. Выполняется расчет Q_ГЭС^пред(Н_а) по следующим формулам:

 

 

ó Н_а³ Н_р^N; Q_ГЭС^пред= (N_ГЭС^уст/ Н_а× K_N),

ô где N_ГЭС^пред= N_ГЭС^уст =const;

Q_ГЭС^пред(Н_а) = í, (5.1)

ï Н_а< Н_р^N; Q_ГЭС^пред=Q_ГЭС^max ×Ö(Н_а/ Н_р^N)

î где N_ГЭС^пред(Н_а)= K_N ×Н_а × Q_ГЭС^пред .

 

Далее, принимается, что Q_ГЭС^пред= Q_нб и определяется Z_нб(Q_ГЭС^пред) по кривой связи (см.табл.5.2). К полученным значениям Z_нб(Q_ГЭС^пред) прибавляется Н_а, соответствующее рассмотренному значению Q_ГЭС^пред (см. табл.5.3), т.е.

 

Z_вб(Н_а, Q_ГЭС^пред) = Z_нб(Q_ГЭС^пред)+ Н_а. (5.2)

 

Таблица 5.3

Расчет координат линии ограничения мощности ГЭС Q_ГЭС^пред(Z_вб, Н_а) и N_ГЭС^пред(Z_вб, Н_а) при K_N=8,2; H_p^N=16м; N_ГЭС^уст=345 МВт

 

На, м
QГЭСпред, м3/с
Zнб,м	85,6	85,68	85,76	85,83	85,7	85,56	85,45
Zвб, м	98,6	99,68	100,76	101,83	102,7	103,56	104,45
NГЭСпред, МВт

 

Значения Z_вб, равное 102,7 м будем далее обозначать через Z_вб⁰. Если Z_вб< Z_вб⁰, то это означает, что расчет ведется в I-ой зоне, где имеет место ограничение по турбине (Н_а< Н_р^N). Для Z_вб >Z_вб⁰ предельная мощность ГЭС равна N_ГЭС^уст=345 МВт. В графическом виде сказанное выше иллюстрировано на рис.5.1.

Рис.5.1

 

5.2.2. Расчет режима работы ГЭС “по водотоку”.

Этому режиму соответствуют следующие основные показатели: Z_вб(t)=const и Q_нб(t)º Q_пр(t).

Последовательность расчета может быть представлена следующим образом: (Z_вб =const;`Q<sub>пр</sub> =const) ® (`Q_пр º`Q<sub>нб</sub>) ® (`Z_нб =`Z<sub>нб</sub>(`Q_пр)) ® (Н_а = Z_вб –`Z<sub>нб</sub>) ® Q<sub>ГЭС</sub><sup>пред</sup>(Н<sub>а</sub>) ® (`Q_ГЭС,`Q<sub>х. сбр</sub>) ® (`N_ГЭС = 8,2·`Q<sub>ГЭС</sub>·Н<sub>а</sub>(`Q_пр).

Расчет режима “по водотоку” при Q_{х. сбр} º 0 для Z_вб =104,0 м; Q_пр =1000 м³/с; все прочие исходные данные соответствуют п.5.1.

В соответствии с представленным алгоритмом получаем: Q_пр = Q_нб =1000 м³/с; Z_нб =83,58 м; Н_а =20,42 м; Q_ГЭС^пред(Н_а)= 2060 м³/с; Q_ГЭС = Q_пр = Q_нб =1000 м³/с; N_ГЭС = 167 МВт.

Расчет режима “по водотоку” при Q_{х. сбр} ¹ 0 для Z_вб =101,0 м; Q_пр =3000 м³/с; все прочие исходные данные соответствуют п.5.1.

По рассмотренному выше получаем: Q_пр = Q_нб =3000 м³/с; Z_нб =86,15 м; Н_а =14,85 м;

Q_ГЭС^пред(Н_а)= Q_ГЭС^max 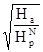= 2630· =2533 м³/с;

Q_ГЭС = Q_ГЭС^пред =2533 м³/с Q_х.сбр= 467 м³/с; N_ГЭС = 308 МВт.

 

5.2.3. Расчет Q_ГЭС^пред и N_ГЭС^пред в заданный момент времени t при Z_вб(t)=const.

Возможны два метода решения поставленной задачи: безитерационный табличный или графический метод и итерационный-численный. В безитерационном методе (наиболее предпочтительном) на основе данных табл.5.3, для любого заданного значения Z_вб(t)=const метод линейной интерполяции рассчитывается Q_ГЭС^пред и далее N_ГЭС^пред.

Например, найти Q_ГЭС^пред и N_ГЭС^пред при Z_вб(t)=const=(103,0 м и 100,0 м). На основе данных табл.5.3 для Z_{вб 1}(t)=103,0 м получаем, что Q_ГЭС^пред и N_ГЭС^пред можно найти по выражениям:

 

Q_ГЭС^пред(Z_{вб 1})= Q_ГЭС^пред(Z_вб = 102,7)+

+ (103,0–102,7) · =

= 2475–0,3·138/0,86= 2427 м³/с.

 

Поскольку Z_{вб 1}(t)>Z_вб⁰, то N_ГЭС^пред º N_ГЭС^уст = 345 МВт.

 

Аналогично для Z_{вб 2}(t)=100,0 м получаем:

 

Q_ГЭС^пред(Z_{вб 2})= Q_ГЭС^пред(Z_вб = 99,68 м) +

+ (100,0–99,68)· =

=2460–0,32·86/1,08= 2485 м³/с.

Поскольку Z_{вб 2}(t)<Z_вб⁰, то N_ГЭС^пред также находим по данным табл.5.3: N_ГЭС^пред (Z_{вб 2})=282+0,32·31/1,08 =291 МВт. N_ГЭС^пред (Z_{вб 2}) можно также рассчитать по следующему алгоритму: (Z_вб2, Q_ГЭС^пред) ® (Q_нб º Q_ГЭС^пред) ® Z_нб(Q_ГЭС^пред) ® (Н_а=Z_{вб 2}–Z_нб) ®

® N_ГЭС^пред = k_N·Q_ГЭС^пред ·Н_а.

Численный итерационный метод решения поставленной задачи базируется на использовании следующего нелинейного алгебраического выражения:

Q_ГЭС^пред(Z_вб)= . (5.3)

 

На рис.5.2. и 5.3. в графическом виде поясняется алгоритм решения поставленной задачи для зоны I и зоны II рис.5.1.

Рис.5.2

 

Рис.5.3

 

Зона I с Z_вб =100,0 м: принимаем в качестве Q_{нб 1} = Q₁ значение Q_ГЭС^max =2630 м³/с. Определяем Z_нб(Q₁) и далее – Н₁ = =100–Z_нб(Q₁). Для (Н_а=Н₁)<Н_р^N определяем Q_ГЭС^пред по (5.1), приравнивая его Q₂. Для Q_ГЭС =Q_нб =Q₂ и Z_вб =100,0 м определяем Z_нб(Q₂) и Н₂ = 100–Z_нб(Q₂). Для (Н_а=Н₂)<Н_р^N определяем Q_ГЭС^пред по (5.1) и приравниваем его Q₄. Оцениваем разницу между Q₂ и Q₄ по формуле:

£e_Q. (5.4)

Если в (5.4) указанная разница меньше e_Q, то решение найдено, т.е. получены для Z_вб =100,0 м: Q_ГЭС^пред, Н_а(Q_ГЭС^пред) и N_ГЭС^пред(Н_а, Q_ГЭС^пред). В противном случае проводится следующая итерация (см.рис.5.2).

Зона II с Z_вб =103,0 м: поиск решения аналогичен рассмотренному выше способу для зоны I (см.рис.5.3).

 

 

5.2.4. Расчет Q_ГЭС^пред и N_ГЭС^пред в заданный момент времени t при известных значениях Z_вб(t)=const и`Q_пр > Q_ГЭС^max.

Очевидно, что в этом случае на ГЭС для поддержания Z_вб(t)=const при`Q<sub>нб</sub> º`Q_пр должны быть Q_х.сбр ¹0 и как следствие этого невозможность использования всех данных табл.5.3, где предполагалось, что Q_ГЭС º Q_нб Q_х.сбрº0. Решение задачи реализуется численным методом (без итерации).

Например, требуется найти Q_ГЭС^пред и N_ГЭС^пред при Z_{вб 1}=103,0 м и Z_{вб 2}=100,0 м и `Q_пр = 3000 м³/с.

Для Z_{вб 1}=103,0 м: (`Q<sub>нб</sub> =`Q_пр)> Q_ГЭС^max. Z_нб(`Q_нб = 3000 м³/с) =86,14 м; Н_а = Z_{вб 1} – Z_нб = 103,0–86,14= 16,86 м при Н_р^N = 16,0 м; Q_ГЭС^пред(Н_а =16,86 м)= 2495 м³/с и N_ГЭС^пред = N_ГЭС^уст = 345 МВт и Q_х.сбр = 505 м³/с.

Для Z_{вб 2}=100,0 м: Н_а = Z_{вб 2} – Z_нб = 100,0–86,14= 13,86 м при Н_р^N = 16,0 м; Q_ГЭС^пред (Н_а =13,86 м)= 2447 м³/с, N_ГЭС^пред = 278 МВт.

 

 

5.2.5. Определение необходимости сработки-наполнения водохранилища при заданных значениях Z_вб^н,`Q<sub>пр</sub> и`N_ГЭС.

Задача решается безитерационным путем в следующей последовательности (см.рис.5.4). В табл.5.4. представлен пример решения задачи для двух значений (Z_вб^н,`Q<sub>пр</sub> и`N_ГЭС).

 

 

Таблица 5.4

Расчет необходимости сработки-наполнения водохранилища при заданных значениях Z_вб^н,`Q<sub>пр</sub> и`N_ГЭС

Zвбн, м	`Qпр, м3/с	`NГЭС, МВт	`Qнб, м3/с	`Zнб, м	На, м	`NГЭСрасч, МВт	сработка-наполнение
104,0				81,00	23,0	37,7	сработка
100,0				82,24	14,76	242,0	наполнение

 

Дано: Z_вб^н,`Q<sub>пр</sub>,`N_ГЭС

¯

Q_ГЭС º`Q_пр

¯

`Z<sub>нб</sub> =`Z_нб(`Q_пр)

¯

Н_а = Z_вб^н –`Z_нб

¯

`N<sub>ГЭС</sub><sup>расч</sup> = k<sub>N</sub>·Н<sub>а</sub>·`Q_пр

¯

`N<sub>ГЭС</sub><sup>расч</sup> ³`N_ГЭС

> = <

 

Q_в<0 Q_в º0 Q_в>0

наполнение сработка

 

Рис.5.4

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: