 |
Решение простейшей задачи ВЭР1
|
|
|
|
Дано: основные исходные данные п.5.1.; Dt=2,63·106 с; Zвбн = 103,0 м;`Qнбтреб = 500 м3/с;`Qпр = 200 м3/с.
Требуется найти: Zвбк,`Zнб,`На,`QГЭС,`NГЭС.
Задача решается безитерационным путем по алгоритму, представленному на рис.5.5. в последовательности, представленной в табл.5.5.
Решение простейшей задачи ВЭР2
Дано: основные исходные данные п.5.1.; Dt=2,63·106 с; Zвбн = 103,0 м; Zвб = 102,0 м;`Qпр = 200 м3/с.
Требуется найти:`Zвб,`Zнб,`На,`QГЭС,`NГЭС.
Задача решается безитерационным путем по алгоритму, представленному на рис.5.6. в последовательности, представленной в табл.5.6.
Дано: Dt, Zвбн,`Qнбтреб,`Qпр при`Qнбтреб >`Qпр.
¯
`Zнб =`Zнб(`Qнбтреб)
¯
`Qв =`Qнбтреб –`Qпр;
¯
DVсрб =`Qв·Dt
¯
Vвк = Vвн(Zвбн) – DVсрб
¯
Zвбк = Zвбк(Vвк)
¯
`На = 0,5·(Zвбн+Zвбк)–`Zнб
¯
QГЭСпред = 
¯
`QГЭС = 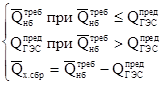
¯
`NГЭС = kN·`QГЭС·`На
Рис.5.5
Дано: Dt, Zвбн, Zвбк,`Qпр при Zвбн > Zвбк.
¯
DVсрб = Vвбн(Zвбн)– Vвбк(Zвбк)
¯
`Qв = 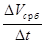
¯
`Qнб =`Qв +`Qпр
¯
`Zнб =`Zнб(`Qнб)
¯
`На = 0,5·(Zвбн+Zвбк)–`Zнб
¯
QГЭСпред = 
¯
`QГЭС = 
¯
`NГЭС = kN·`QГЭС·`На
Рис.5.6
Решение простейшей задачи ВЭР3
Дано: основные исходные данные п.5.1.; Dt=2,63·106 с; Zвбн = 103,0 м;`NГЭС = 100 МВт;`Qпр = 200 м3/с; eN=5%.
Требуется найти: Zвбк,`Zнб,`Qв,`QГЭС,`Qнб,`На,`NГЭС.
Задача решается итерационным путем с использованием алгоритма на рис.5.6 для задаваемых вариантов Zвбк, рассчитываемых значений`NГЭСрасч и сопоставлением их с`NГЭС с точностью до eN.
Вначале решается задача 5.2.4.: Zвбн = 103,0 м;`Qпр =`Qнб = 200 м3/с;`Zнб = 81,00 м; НГЭС =Zвбн –`Zнб = 22,0 м;`NГЭСрасч = 8,2·22,0´ ´ 0,2 = 36 МВт, следовательно, требуется сработка водохранилища.
Расчет для нескольких вариантов Zвбк проводится в форме табл.5.6. с добавлением необходимых расчетных переменных и сопоставлением`NГЭСрасч(Zвбк) с заданным значением`NГЭС (см. табл.5.7).
|
|
|
Для поиска решения задачи используется графический способ, реализованный ранее в решении водохозяйственных задач на рис.4.1., 4.2. (см.рис.5.7).
На рис. 5.7 получена т.А с Zквб= 101,85 м для которой выполнены все расчеты в табл.5.7, соответствующее искомому решению задачи ВЭР3.

Рис. 5.7
Обобщение задач ВЭР1 и ВЭР2
5.6.1. ВЭР1.1: работа ГЭС с Qнбтреб > QГЭСпред (Zвб) с обеспечением NГЭС Þ max.
Дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=104,0 м; Qпр=2200 м3/с; Qнбтреб=2800 м3/с; eQ=4%.
Требуется найти: Zвбк, QГЭС, Hаi, NГЭС, Qх.сбр., Qв. Решение задачи реализуется итерационным путем и поясняется в табл.5.8 и на рис. 5.8.
Решение задачи: Zвбк=103,2 м; QГЭСпред=2335 м3/с; Qв=623 м3/с; Qх.сбр=465 м3/с; NГЭСmax= NГЭСуст=345 МВт; Qнбфакт=2800 м3/с.
5.6.2. ВЭР2.1: работа ГЭС предельными мощностями с Qх.сбр¹0.
Дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=102,0 м; Zвбк=100,0 м;Qпр=2100 м3/с.
Требуется найти: Qвi, QГЭСпред, Qх.сбр, NГЭСпред, Hа.
Решение задачи реализуется безитерационным путем и поясняется в табл.5.9.

Рис. 5.8
Обобщение задачи ВЭР3
5.7.1. ВЭР3.1: сработка водохранилища по критерию NГЭС Þ max в зонах I и II.
Для зоны II дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=104,0 м; Qпр=2000 м3/с.
Требуется найти: Zвбк, Qв, QГЭС, NГЭС, Qх.сбр., Qв по критерию NГЭС Þ max при eQ=2%.
Поиск решения осуществляется в зоне II методом простых итераций и поясняется в табл.5.10 и на рис.5.9.
Координаты решения: Zвбк=103,65 м; Qв=296 м3/с; QГЭСпред=2300 м3/с; NГЭСпред= NГЭСуст=345 МВт.
Для зоны I дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=101,7 м; Qпр=2200 м3/с.
Требуется найти: Zвбк, Qв, QГЭС, NГЭС по критерию NГЭС Þ max при eQ=2%.
Поиск решения осуществляется в зоне I методом простых итераций и поясняется в табл.5.11.
Координаты точки решения: Zвбк=100,5 м; Qв=365 м3/с; QГЭСпред= Qнб=2570 м3/с; NГЭСпред= 322 МВт, На=15,32 м.
|
|
|

Рис. 5.9
5.7.2. ВЭР3.2: Расчет режима наполнения водохранилища по критерию NГЭС Þ max в зоне I.
Дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=100,0 м; Qпр=3000 м3/с; Zвб0=101,83 м.
Требуется найти: Zвбк, Qв, QГЭС, Qнб, Hа, NГЭС по критерию NГЭС Þ max при eQ=2%.
Поиск решения осуществляется итерационным путем методом простых итераций и поясняется расчетами в табл.5.12 и на рис.5.10.

Рис. 5.10
Так как Qпр > QГЭСmax, то реализуется режим наполнения в зоне I (Zвбн < Zвб0) с переменными значениями QГЭСпред(Zвб) и NГЭСпред(Zвб).
Предварительно определяются предельные параметры ГЭС при Zвбн=100,0 м: QГЭСпред=2485 м3/с; Zнб(QГЭСпред)=85,70 м; На=14,3 м; NГЭСпред = 8,2× QГЭСпред × На=291 МВт. Соответственно: Qвн = Qпр - QГЭСпред =515 м3/с. Это значение и принимается в табл.5.12 за Qв1, для которого и выполняются все расчеты для первой итерации в следующей последовательности:
(DVнап1 = Qв1×Dt) ® (Vвк1 = Vвн(Zвбн) + DVнап1) ® Zвбк1 ®
® Zвб1® QГЭСпред1(Zвб1) ® (Qв1расч = Qпр - QГЭСпред1) ®
® [ dQ=| (Qв1- Qв1расч)/ Qв1| ] £ eQ.
Если dQ £ eQ, то решение найдено. В противном случае следует задаваться новым значением Zвбк2¹ Zвбк1 и продолжать поиск решения в последовательности, указанной в табл.5.12. Из результатов первой итерации видно, что Qв>Qврасч, т.е. Zвбк2 должно быть меньше, чем Zвбк1=101,79 м, что и сделано в табл.5.12. Поиск Zвбк2 можно даже реализовать и для Qв2 = 0,5×(Qв1+ Qврасч1) = 480 м3/с.
Для двух итераций в табл.5.12 получены условия, говорящие о том, что решение задачи находится в интервале Zвбк от 101,50 до 101,79 м. Поиск решения (т.А) показан на рис.5.10 и в табл.5.12. Координаты точки решения: Zвбк=101,62 м; Qв=452 м3/с; QГЭС=2548 м3/с; Zнб(Qнб)=85,76 м; Zвб=100,81 м; На=15,05 м и NГЭС =314 МВт. При этом Zвбк < Zвб0, т.е. решение задачи реализовано в зоне I корректно для заданного Dt и предположением, что линия ограничения QГЭСпред(Zвб) в зоне от Zвбн до Zвбк - линейна. Если же указанная характеристика - нелинейна, то процесс поиска решения остается тот же, однако при этом следует проводить расчеты с Dt1< Dt. Например, вместо месячного интервала Dt=2,63×106 c следует брать декадные или Dt1=1/3×Dt.
5.7.3. ВЭР3.3: Расчет режима наполнения водохранилища по критерию NГЭС Þ max в зоне II.
Дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=102,0 м; Qпр=3000 м3/с; Zвб0=101,83 м
|
|
|
Требуется найти: Zвбк, Qв, QГЭС, Qнб, Hа, NГЭС по критерию NГЭС Þ max при eQ=2%.
Поиск решения осуществляется итерационным путем методом простых итераций и поясняется расчетами в табл.5.13 и на рис.5.11.

Рис. 5.11
Как и в предыдущем случае при Qпр > QГЭСmax реализуется режим наполнения, но уже в зоне II (Zвбн > Zвб0) с переменными значениями QГЭСпред(Zвб) при NГЭСпред(Zвб)= NГЭСуст=сonst при На>HpN.
Предварительно определяются предельные параметры ГЭС при Zвбн=102,0 м: QГЭСпред=2600 м3/с; Zнб(QГЭСпред)=85,80 м; На=16,19 м; NГЭСпред = NГЭСуст=345 МВт. Соответственно: Qвн = = Qпр - QГЭСпред = 3000-2600 = 400 м3/с. Это значение и принимается в табл.5.12 за Qв1, для которого выполняются все расчеты в последовательности, указанной выше в п.5.7.2.
По результатам первой итерации получено, что Qв1< Qв1расч, т.е в качестве Zвбк2 следует брать значение, больше Zвбк1=103,1 м, что и реализовано в табл.5.13.
5.7.4. ВЭР3.4: Расчет режима наполнения водохранилища по критерию NГЭС Þ max при переходе из зоны I в зону II.
Дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=101,5 м; Qпр=3000 м3/с; Zвб0=101,83 м
Требуется найти: Zвбк, Qв, QГЭС, Qнб, Hа, NГЭС по критерию NГЭС Þ max при eQ=2%.
Поиск решения осуществляется итерационным путем в последовательности, аналогичной представленной в п.5.7.2 и 5.7.3. с учетом возможности перехода из зоны I в зону II.
Действительно, для Zвбн=101,5 м имеем следующие предельные параметры режима ГЭС: QГЭСпред=2600 м3/с; Zнб(QГЭСпред)=85,80 м; На=16,19 м; NГЭСпред = NГЭСуст=345 МВт. Соответственно: Qв1 = Qпр - QГЭСпред = 400 м3/с, DVнап1= Qв1×Dt=1,05×109 м3; Vвбк1 = Vвбн(Zвбн) + DVнап1 =(4,92+1,05) ×109 =5,97×109 м3; Zвбк1=102,58 м.
Полученное значение Zвбк1=102,58 м больше, чем Zвб0=101,83 м, т.е. произошел переход режима ГЭС из зоны I в зону II, что требует изменения порядка расчета.
В начале рассматривается расчет ВЭР для заданных значений Zвбн=101,5 м и Zвбк1= Zвб0=101,83 м при Qпр =3000 м3/с в последовательности рассмотренной выше и представленной в табл.5.14.
В табл.5.14 значение Dt1 определяется по формуле:
Dt1= [Vвбк(Zвб0) - Vвбн(Zвбн)]/ Qв, (5.5)
где
Qв = Qпр - QГЭСпред , (5.6)
|
|
|
при
QГЭСпред =0,5× [QГЭСпред.к(Zвб0)+ QГЭСпред.н(Zвбн)]. (5.7)
Здесь: QГЭСпред.к(Zвб0)= QГЭСmax=2630 м3/с.
Во время режима наполнения водохранилища предельными мощностями в зоне I получаем следующие параметры режима:
QГЭСпред(Zвбн)=2600 м3/с; Zнб(QГЭСпред)=85,90 м;
На= Zвбн - Zнб(QГЭСпред)=15,6 м; NГЭСпред(Zвбн)=332 МВт; соответственно для Zвбк1= Zвб0=101,83 м получаем, что с QГЭСпред= =QГЭСmax = 2630 м3/с; На= НрN=16 м и NГЭСпред= NГЭСуст=345 МВт.
Далее рассматривается новая задача, где Zвбн1= Zвб0=101,83 м; Dt2=Dt - Dt1=1,8×106 с; Qпр=3000 м3/с и требуется найти оконча-тельные параметры режима наполнения.
Расчет производится по алгоритму, аналогичному рассмотренному в п.5.7.3 для ВЭР3.3 с Dt2¹Dt (см.табл.5.15, рис.5.12).
Координаты окончательного решения: Zвбк=102,66 м; Dt2=1,8×106 с; QГЭСпред = 2555 м3/с; Zнб(QГЭСпред) = 85,77 м; На= Zвб - Zнб=102,24 - 85,77 =16,47 м; NГЭСпред= NГЭСуст=345 МВт. Графики изменения Zвб(t) и NГЭСпред(t) показаны на рис.5.13.
|

Рис. 5.12
Рис. 5.13
5.7.5. ВЭР3.5: Расчет режима наполнения водохранили-ща с Zвбн до НПУ по двум способам: равномерный режим наполнения до НПУ за Dt и максимально быстрое наполнение до НПУ с Qх.сбр.=0 за Dt1<Dt.
Дано: основные исходные данные приведены в п.5.1; Dt=2,63×106 c; Zвбн=103,0 м; Qпр=4000 м3/с.
Требуется найти: Zвб(t), Qв(t), QГЭС(t), NГЭС(t) по двум указанным выше критериям.
Режим равномерного заполнения от Zвбн=103,0 м до НПУ=104,0 м: последовательность безитерационного расчета представлена в табл.5.16. В связи с тем, что в этих расчетах при Qх.сбр.¹0 и Qнб(t)= QГЭС(t)+ Qх.сбр.(t) нельзя пользоваться данными табл.5.3.
Режим максимально быстрого наполнения с Zвбн=103,0 м до НПУ с Qх.сбр.=0 за Dt2<Dt: по данным табл.5.16 имеем DVнаптреб=1,84×109 м3 и QГЭСпред(Zвб=103,5 м)=2345 м3/с при Qх.сбр.=0 по данным табл. 5.3.
Соответственно: Qв = Qпр - QГЭСпред=4000-2345=1655 м3/с и Dt1=DVнаптреб/ Qв= 1,84×109/1655=1,11×106 с =12,84 суток.
Параметры полученного режима: Zвбн=103,0 м Zвбк= = НПУ=104,0 м; Qнб=QГЭСпред= 2345 м3/с; Zнб(QГЭСпред) =85,58 м; На= Zвб - Zнб=17,92 м; NГЭС= NГЭСуст=345 МВт; Dt1=1,11×106 с =12,84 суток.
В оставшийся период времениDt2=Dt - Dt1 = 1,52×106 с ГЭС работает по водотоку с Qнб= Qпр и Qв=0 при Qх.сбр.¹0. Расчет этого режима работы представлен в табл.5.17.
Таблица 5.17
Расчет режима работы ГЭС "по-водотоку" при НПУ=соnst=104,0 м
| Zвб, м | Qпр, м3/с | Qнб, м3/с | Zнб, м | Ha, м | QГЭСпред, м3/с | NГЭСпред, МВт | Qх.сбр, м3/с |
| 104,0 | 86,85 | 17,15 |
В графическом виде полученный режим работы ГЭС по двум рассмотренным способам представлен на рис. 5.14 а) и б) соответственно.

Рис. 5.14
|
|
|



