 |
Раздел I. Дифференциальное исчисление функции одной переменной.
|
|
|
|
1. Найти производную  :
:
1.1. а)  б)
б)  в)
в) 
1.2. а)  б)
б)  в)
в) 
1.3. а)  б)
б)  в)
в) 
1.4. а)  б)
б)  в)
в) 
1.5. а)  б)
б)  в)
в) 
1.6. а)  б)
б)  в)
в) 
1.7. а)  б)
б)  в)
в) 
1.8. а)  б)
б)  в)
в) 
1.9. а)  б)
б)  в)
в) 
1.10. а)  б)
б)  в)
в) 
1.11. а)  б)
б)  в)
в) 
1.12. а)  б)
б)  в)
в) 
1.13. а)  б)
б)  в)
в) 
1.14. а)  б)
б)  в)
в) 
1.15. а)  б)
б)  в)
в) 
1.16. а)  б)
б)  в)
в) 
1.17. а)  б)
б)  в)
в) 
1.18. а)  б)
б)  в)
в) 
1.19. а)  б)
б)  в)
в) 
1.20. а)  б)
б)  в)
в) 
1.21. а)  б)
б)  в)
в) 
1.22. а)  б)
б) 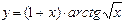 в)
в) 
1.23. а)  б)
б)  в)
в) 
1.24. а)  б)
б)  в)
в) 
1.25. а)  б)
б)  в)
в) 
1.26. а)  б)
б)  в)
в) 
1.27. а) 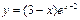 б)
б)  в)
в) 
1.28. а)  б)
б)  в)
в) 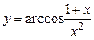
1.29. а)  б)
б)  в)
в) 
1.30. а)  б)
б)  в)
в) 
2. Найти а) производную функции  , заданной параметрически; б) производную функции
, заданной параметрически; б) производную функции  , заданной неявно.
, заданной неявно.
2.1.а)  ,
,  б)
б) 
2.2. а)  ,
,  б)
б) 
2.3. а)  ,
,  б)
б) 
2.4. а)  ,
,  б)
б) 
2.5. а)  ,
,  б)
б) 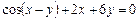
2.6. а)  ,
,  б)
б) 
2.7. а)  ,
,  б)
б) 
2.8. а)  ,
, 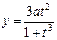 б)
б) 
2.9. а)  ,
,  б)
б) 
2.10. а)  ,
,  б)
б) 
2.11. а)  ,
,  б)
б) 
2.12.а)  ,
,  б)
б) 
2.13.а)  ,
,  б)
б) 
2.14.а)  ,
,  б)
б) 
2.15.а)  ,
,  б)
б) 
2.16.а)  ,
,  б)
б) 
2.17.а)  ,
,  б)
б) 
2.18.а) 
 , б)
, б) 
2.19.а)  ,
,  б)
б) 
2.20.а)  ,
,  б)
б) 
2.21.а)  ,
,  б)
б) 
2.22.а)  ,
,  б)
б) 
2.23.а)  ,
,  б)
б) 
2.24.а)  ,
,  б)
б) 
2.25.а)  ,
,  б)
б) 
2.26.а)  ,
,  б)
б) 
2.27.а)  ,
,  б)
б) 
2.28.а)  ,
,  б)
б) 
2.29. а)  ,
,  б)
б) 
2.30. а)  ,
,  б)
б) 
3. Вычислить пределы, используя правило Лопиталя.
3.1. а)  б)
б)  в)
в) 
3.2. а)  б)
б)  в)
в) 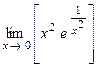
3..3. а)  б)
б)  в)
в) 
3.4. а)  б)
б)  в)
в) 
3..5. а)  б)
б)  в)
в) 
3.6. а)  б)
б)  в)
в) 
3.7. а)  б)
б)  в)
в) 
3.8. а)  б)
б)  в)
в) 
3.9. а)  б)
б)  в)
в) 
3.10. а) 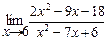 б)
б)  в)
в) 
3.11. а)  б)
б)  в)
в) 
3.12. а)  б)
б)  в)
в) 
3.13 а)  б)
б)  в)
в) 
3.14. а)  б)
б)  в)
в) 
3.15. а)  б)
б)  в)
в) 
3.16. а)  б)
б)  в)
в) 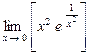
3.17. а)  б)
б)  в)
в) 
3.18. а)  б)
б)  в)
в) 
3.19. а)  б)
б)  в)
в) 
3.20 а)  б)
б)  в)
в) 
3.21. а)  б)
б)  в)
в) 
3.22. а)  б)
б)  в)
в) 
3.23. а)  б)
б)  в)
в) 
3.24. а)  б)
б) 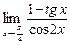 в)
в) 
3.25. а)  б)
б)  в)
в) 
3.26. а)  б)
б)  в)
в) 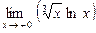
3.27. а)  б)
б)  в)
в) 
3.28. а)  б)
б)  в)
в) 
3.29. а)  б)
б)  в)
в) 
3.30. а)  б)
б)  в)
в) 
4. Для указанной функции  требуется провести полное исследование функции и построить её график.
требуется провести полное исследование функции и построить её график.
4.1.  4.2.
4.2. 
4.3.  4.4.
4.4. 
4.5.  4.6.
4.6. 
4.7.  4.8.
4.8. 
4.9.  4.10.
4.10. 
4.11.  . 4.12.
. 4.12.  .
.
4.13.  . 4.14.
. 4.14.  .
.
4.15.  4.16.
4.16. 
4.17.  4.18.
4.18. 
4.19.  4.20.
4.20. 
4.21.  4.22.
4.22. 
4.23.  4.24.
4.24. 
4.25.  4.26.
4.26. 
4.27.  4.28.
4.28. 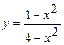
4.29.  4.30.
4.30. 
5. Н айти наибольшее и наименьшее значения функции  на отрезке
на отрезке  .
.
5.1.  , [0; 2].
, [0; 2].
5.2.  , [-2; 1]
, [-2; 1]
5.3.  , [0,5; 2]
, [0,5; 2]
5.4.  , [-1; 1]
, [-1; 1]
5.5.  , [1; 3]
, [1; 3]
5.6.  , [0; 3]
, [0; 3]
5.7.  , [-2; 2]
, [-2; 2]
5.8.  , [-4; -2]
, [-4; -2]
5.9. 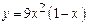 , [0,5; 1]
, [0,5; 1]
5.10. 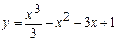 , [-2; 0]
, [-2; 0]
5.11.  , [-6; -2]
, [-6; -2]
|
|
|
5.12.  , [-1; 1]
, [-1; 1]
5.13.  , [2; 4]
, [2; 4]
5.14.  , [2; 6]
, [2; 6]
5.15.  , [-1; 2]
, [-1; 2]
5.16.  , [0; 2]
, [0; 2]
5.17.  , [1; 3]
, [1; 3]
5.18.  , [0; 1]
, [0; 1]
5.19.  , [1; 5]
, [1; 5]
5.20.  , [0; 3]
, [0; 3]
5.21.  , [0; -1]
, [0; -1]
5.22.  , [2; 4]
, [2; 4]
5.23.  , [-1; 2]
, [-1; 2]
5.23.  , [0; 3]
, [0; 3]
5.24.  , [-2; -0,5]
, [-2; -0,5]
5.25.  , [-2; 0]
, [-2; 0]
5.26.  , [0,1; 1]
, [0,1; 1]
5.27.  , [-3; 0]
, [-3; 0]
5.29.  , [-1; 1]
, [-1; 1]
5.30.  , [1; 4]
, [1; 4]
Раздел II. Функции нескольких переменных.
6. Для указанной функции  требуется: найти а) полный дифференциал
требуется: найти а) полный дифференциал  ; б) смешанную производную
; б) смешанную производную  .
.
6.1.  , 6.2.
, 6.2.  ,
,
6.3.  , 6.4.
, 6.4. 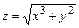 ,
,
6.5.  , 6.6.
, 6.6.  , 6.7.
, 6.7.  , 6.8.
, 6.8. 
6.9.  6.10.
6.10. 
6.11.  6.12.
6.12. 
6.13.  6.14.
6.14. 
6.15.  6.16.
6.16. 
6.17.  6.18.
6.18. 
6.19.  6.20.
6.20. 
6.21.  6.22.
6.22. 
6.23.  6.24.
6.24. 
6.25.  6.26.
6.26. 
6.27.  6.28.
6.28. 
6.29.  6.30.
6.30. 
7. Для функции  , заданной неявно, найти частные производные
, заданной неявно, найти частные производные  и
и  .
.
7.1  7.2.
7.2. 
7.3.  7.4.
7.4. 
7.5.  7.6.
7.6. 
7.7.  7.8.
7.8. 
7.9. 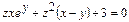 7.10.
7.10.  7.11.
7.11.  7.12.
7.12.  7.13.
7.13.  7.14.
7.14.  7.15.
7.15.  7.16.
7.16.  7.17.
7.17.  7.18.
7.18.  7.19.
7.19.  7.20.
7.20.  7.21.
7.21.  7.22.
7.22.  7.23.
7.23. 
7.24. 
7.25. 
7.26. 
7.27.  7.28.
7.28.  7.29.
7.29.  7.30.
7.30. 
8. Найти локальные экстремумы функции 
8.1.  8.2.
8.2.  ,
, 
8.3.  8.4.
8.4.  ,
, 
8.5.  ,
,  8.6.
8.6. 
8.7.  8.8.
8.8. 
8.9.  8.10.
8.10. 
8.11.  . 8.12.
. 8.12. 
8.13.  8.14.
8.14. 
8.15.  8.16.
8.16. 
8.17.  8.18.
8.18. 
8.19.  8.20.
8.20. 
8.21.  8.22.
8.22. 
8.23.  8.24.
8.24. 
8.25. 
8.26.  8.27.
8.27. 
8.28.  8.29.
8.29. 
8.30. 
9. Найти условные экстремумы функции  (методом Лагранжа):
(методом Лагранжа):
9.1.  при
при 
9.2.  при
при 
9.3.  при
при 
9.4.  при
при 
9.5.  при
при 
9.6.  при
при 
9.7.  при
при 
9.8.  при
при 
9.9.  при
при 
9.10.  при
при 
9.11.  при
при 
9.12.  при
при 
9.13.  при
при 
9.14.  при
при 
9.15.  при
при 
9.16.  при
при 
9.17.  при
при 
9.18.  при
при 
9.19.  при
при 
9.20. 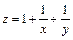 при
при 
9.21.  при
при 
9.22.  при
при 
9.23.  при
при 
9.24.  при
при 
9.25.  при
при 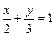
9.26.  при
при 
9.27.  при
при 
9.28.  при
при 
9.29.  при
при 
9.30.  при
при 
10. Найти наибольшее и наименьшее значения функции  в ограниченной и замкнутой области D:
в ограниченной и замкнутой области D:
10.1.  ,
,  .
.
10.2.  ,
, 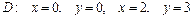 .
.
10.3.  ,
,  .
.
10.4.  ,
,  .
.
10.5. 
 .
.
10.6.  ,
,  .
.
10.7.  ,
,  .
.
10.8.  ,
,  .
.
10.9.  ,
,  .
.
10.10.  ,
,  .
.
10.11.  ,
,  .
.
10.12.  ,
, 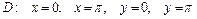 .
.
10.13.  ,
,  .
.
10.14.  ,
,  .
.
10.15.  ,
,  .
.
10.16.  ,
,  .
.
10.17.  ,
,  .
.
10.18.  ,
,  .
.
10.19.  ,
,  .
.
10.20.  ,
,  .
.
10.21.  ,
,  .
.
10.22.  ,
,  .
.
10.23.  ,
,  .
.
10.24.  ,
,  .
.
10.25.  ,
,  .
.
10.26.  ,
,  .
.
10.27.  ,
,  .
.
10.28.  ,
,  .
.
10.29.  ,
,  .
.
10.30.  ,
,  .
.
11. Найти: а) координаты градиента функции  в точке
в точке  ; б) уравнения касательной плоскости и нормали к поверхности, заданной уравнением
; б) уравнения касательной плоскости и нормали к поверхности, заданной уравнением  в точке
в точке  .
.
11.1 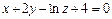 ,
, 
11.2.  ,
, 
11.3.  ,
, 
11.4.  ,
, 
11.5.  ,
, 
11.6..  ,
, 
11.7..  ,
, 
11.8.  ,
, 
11.9.  ,
, 
11.10.  ,
, 
11.11.  ,
, 
11.12.  ,
, 
11.13.  ,
, 
11.14.  ,
, 
11.15.  ,
, 
11.16.  ,
, 
|
|
|


