 |
Раздел II. Функции нескольких переменных.
|
|
|
|
23. N-мерная точка, n-мерное арифметическое пространство  . Расстояние в
. Расстояние в  . N-мерный шар. Окрестность точки в
. N-мерный шар. Окрестность точки в  . Классификация точек (предельные, внутренние, граничные). Множества точек в
. Классификация точек (предельные, внутренние, граничные). Множества точек в  (открытые, замкнутые, ограниченные, связные, выпуклые).
(открытые, замкнутые, ограниченные, связные, выпуклые).
24. Понятие функции 2-х переменных, n-переменных. Естественная область определения ФНП, график функции 2-х переменных, линии и поверхности уровня.
25. Частные и полное приращения ФНП. Понятия предела и непрерывности ФНП. Свойства функций непрерывных в ограниченной и замкнутой области.
26. Частные производные первого и высших порядков, их нахождение.
27. Понятие дифференцируемости ФНП в точке. Независимость смешанных производных от порядка дифференцирования.
28. Взаимосвязь понятий: дифференцируемость ФНП в точке, непрерывность в точке, существование в точке конечных частных производных.
29. Геометрический смысл дифференцируемости ФНП в точке. Уравнения касательной плоскости и нормали к поверхности в данной точке.
30. Дифференциалы ФНП первого и высших порядков, их нахождение. Применение первого дифференциала в приближённых вычислениях.
31. Производная по направлению и градиент, связь между ними.
32. Неявная ФНП, условия её существования и дифференцируемости. Правила вычисления производных неявной функции.
33. Точки локального экстремума (максимума и минимума) и локальные экстремумы ФНП. Стационарные и критические точки. Необходимое и достаточное условия локального экстремума ФНП.
34. Условный экстремум ФНП. Функция Лагранжа. Нахождение условного экстремума методом неопределённых множителей Лагранжа.
35. Глобальные экстремумы (наибольшее и наименьшее значения) ФНП в ограниченной и замкнутой области, их нахождение.
|
|
|
Приложения.
6.1. Образец решения контрольных задач типового варианта.
Семестр 2.
1.1-30. Найти производную  :
:
а)  ; б)
; б) 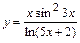 ; в)
; в) 
Нахождение производной  функции
функции  заданной явно, с помощью правил дифференцирования:
заданной явно, с помощью правил дифференцирования:
 (
( ),
),  ,
, 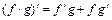 ,
,  ,
,  ,
,  ,
, 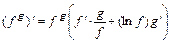 ,
,  сводят к нахождению табличных производных.
сводят к нахождению табличных производных.
Производную  функции
функции  заданной параметрическими уравнениями
заданной параметрическими уравнениями  находят в параметрическом виде по формуле
находят в параметрическом виде по формуле  .
.
Решение.
а)  , где
, где
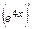
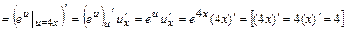 =
=  ;
; 



Тогда  .
.
б)  , где
, где




 .
.
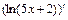


 .
.
Тогда 
 .
.
в) 
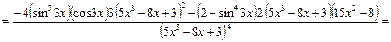
 .
.
Ответ: а)  б)
б)  .
.
в) 
2.1-30. Найти а) производную функции  , заданной параметрически; б) производную функции
, заданной параметрически; б) производную функции  , заданной неявно.
, заданной неявно.
а) Производную функции  , заданной параметрическими уравнениями
, заданной параметрическими уравнениями  находим по формуле
находим по формуле  , где
, где

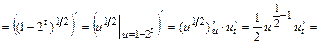

 ;
;
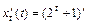

 .
.
Тогда  .
.
б) Уравнение  неявно определяет функцию
неявно определяет функцию  . Дифференцируя его по x, получим:
. Дифференцируя его по x, получим: 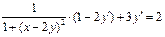 .
.
Выразим 
 ;
;
 .
.
Ответ: а)  б)
б)  .
.
3.1-30. Вычислить пределы, используя правило Лопиталя.
а)  ; б)
; б)  ; в)
; в)  .
.
Вычисление предела 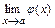 , где
, где  , всегда начинают с подстановки в
, всегда начинают с подстановки в  предельного значения её аргумента
предельного значения её аргумента 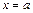 . Если в результате получают неопределённость
. Если в результате получают неопределённость  или
или  , то для её раскрытия применяют правило Лопиталя:
, то для её раскрытия применяют правило Лопиталя:  , где
, где  и
и  - функции, дифференцируемые в окрестности
- функции, дифференцируемые в окрестности  . В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:
. В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:  ,
,  ,
, 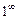 ,
,  ,
,  путём преобразований:
путём преобразований:  ,
,  ,
, 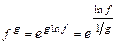 сводят к раскрытию неопределенностей вида
сводят к раскрытию неопределенностей вида  или
или 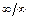 .
.
Решение.
а) 
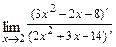 , где
, где


 ,
,



Тогда 
 .
.
б) 
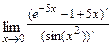 , где
, где
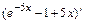


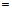
 ,
,


 .
.
Тогда 
 . Применяем правило Лопиталя ещё раз:
. Применяем правило Лопиталя ещё раз: 
 , где
, где

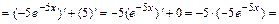
 ,
,


 =
= 
 .
.
Тогда 
 .
.
в)  . Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду
. Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду  , после чего применим правило Лопиталя. Получим
, после чего применим правило Лопиталя. Получим 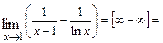
= 
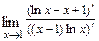 , где
, где


 ,
,


 .
.
Тогда 

 .
.
Применяем правило Лопиталя ещё раз:
|
|
|

 , где
, где 

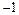 ,
,



 .
.
В итоге получим 
 .
.
Ответ:
а)  ; б)
; б)  ;в)
;в) 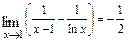 .
.
4.1-30. Для указанной функции  требуется провести полное исследование функции и построить её график:
требуется провести полное исследование функции и построить её график:
 ;
;
Для построения графика функции  нужно:
нужно:
1) найти область определения функции;
2) найти область непрерывности функции и точки разрыва;
3) исследовать функцию на чётность, нечётность и периодичность;
4) найти точки пересечения графика с осями координат;
5) найти асимптоты графика функции;
6) найти интервалы возрастания и убывания, экстремумы функции;
7) найти интервалы выпуклости, вогнутости и точки перегиба.
Решение.
1) Находим область определения функции: 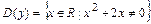 =
=  ).
).
2) Поскольку данная функция является элементарной, то областью её непрерывности является область определения  , а точками разрыва являются точки
, а точками разрыва являются точки  и
и  , не принадлежащие множеству
, не принадлежащие множеству  , но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках
, но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках  и
и  , вычислив в них односторонние пределы функции:
, вычислив в них односторонние пределы функции:
 ,
,  ,
,
 ,
,  .
.
Так как односторонние пределы функции в точках  и
и  - бесконечные, то данные точки являются точками бесконечного разрыва.
- бесконечные, то данные точки являются точками бесконечного разрыва.
3) Функция не является периодической.
Функция  , в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
, в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
Проверяем является ли функция чётной или нечётной. Так как область определения функции  =
=  ) не симметрична относительно точки
) не симметрична относительно точки  , то данная функция – общего вида.
, то данная функция – общего вида.
4) Находим точки пересечения графика с осями координат.
Так как 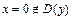 , то точек пересечения графика с осью
, то точек пересечения графика с осью  нет.
нет.
Положим  и решим уравнение
и решим уравнение  . Его решением является
. Его решением является  . Следовательно, точка
. Следовательно, точка  - точка пересечения графика с осью
- точка пересечения графика с осью  .
.
5) Находим вертикальные и наклонные асимптоты графика функции.
Прямая  является вертикальной асимптотой, тогда и только тогда, когда
является вертикальной асимптотой, тогда и только тогда, когда 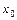 является точкой бесконечного разрыва функции
является точкой бесконечного разрыва функции  .
.
Так как точки  и
и  - точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые
- точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые  и
и  .
.
Прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  при
при  тогда и только тогда, когда одновременно существуют конечные пределы:
тогда и только тогда, когда одновременно существуют конечные пределы:  и
и 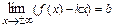 .
.
Вычисляем сначала пределы при  :
:  ,
, 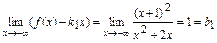 .
.
|
|
|
В дальнейшем будем иметь в виду следующий часто встречающийся предел: 
Следовательно  , т.е.
, т.е.  - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
Аналогично вычисляем пределы при  :
:  ,
,  Следовательно
Следовательно  , т.е.
, т.е.  - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
6) Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:



и определяем критические точки функции  , т.е. точки
, т.е. точки  в которых
в которых 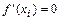 или
или  не существует:
не существует:


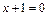

 ;
;
 не существует при
не существует при 

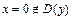 и
и 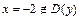 .
.
Таким образом, единственной критической (стационарной) точкой функции  является точка
является точка 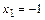 .
.
Исследуем знак производной  в интервалах, на которые критические точки функции
в интервалах, на которые критические точки функции  разбивают её область определения
разбивают её область определения  , и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
, и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:

| 
| 
| 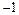
| 
| 
|

| + | + | 
| 
| 
|

| возрастает | возрастает | 
| убывает | убывает |
Так как при переходе слева направо через точку  производная
производная  меняет знак с «+» на «
меняет знак с «+» на « », то точка
», то точка  является точкой локального максимума и
является точкой локального максимума и  .
.
7) Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:


и определяем точки возможного перегиба  , т.е. точки
, т.е. точки  в которых
в которых 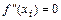 или
или  не существует:
не существует:  , так как
, так как  (квадратное уравнение не имеет действительных корней);
(квадратное уравнение не имеет действительных корней); 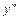 не существует при
не существует при 

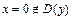 и
и 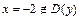 .
.
Таким образом, функция  не имеет точек возможного перегиба.
не имеет точек возможного перегиба.
Исследуем знак второй производной  в интервалах, на которые точки возможного перегиба функции
в интервалах, на которые точки возможного перегиба функции  разбивают её область определения
разбивают её область определения  , и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим следующей таблицей:
, и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим следующей таблицей:

| 
| 
| 
|
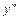
| + | 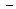
| + |

| график вогнутый | график выпуклый | график вогнутый |
Точек перегиба нет.
8) На основании полученных результатов строим график функции (рис.3)

Рис.3.
Ответ: Рис.3.
5.1-30. Для указанной функции  требуется найти наибольшее и наименьшее значения функции на отрезке
требуется найти наибольшее и наименьшее значения функции на отрезке  :
:
 ,
, 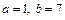 .
.
Наибольшее и наименьшее значения функции  непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке
непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке  достигается или в точках
достигается или в точках  , в которых
, в которых 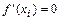 или
или  не существует, или на концах отрезка.
не существует, или на концах отрезка.
|
|
|
1) Находим первую производную функции:
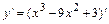

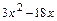
и определяем внутренние критические точки функции  , т.е. точки
, т.е. точки 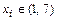 в которых
в которых 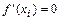 или
или  не существует:
не существует:


 , точек
, точек 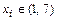 в которых
в которых  не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции
не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции  на отрезке
на отрезке  является точка
является точка  .
.
2) Вычисляем значения функции  во внутренних критических точках и на концах отрезка
во внутренних критических точках и на концах отрезка  :
:  ,
, 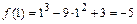 ,
,  .
.
3) Сравниваем значения  ,
,  ,
,  и находим наименьшее и наибольшее значения функции
и находим наименьшее и наибольшее значения функции  на отрезке
на отрезке  :
:
 ,
,  .
.
Ответ:  ,
, 
6.1 – 30. Для указанной функции  требуется: а) найти полный дифференциал
требуется: а) найти полный дифференциал  ; б) вторую частную (смешанную) производную
; б) вторую частную (смешанную) производную  ; если
; если  .
.
Полный дифференциал функции  имеет вид
имеет вид  .
.
Частные производные функции  вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу
вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу  (аргументу
(аргументу  ), то другой аргумент
), то другой аргумент  (аргумент
(аргумент  ) считается постоянным.
) считается постоянным.
Решение.
а) Находим частные производные первого порядка  и
и  функции
функции
 :
: 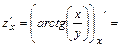


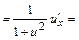
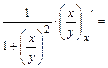

 ;
;






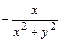 .
.
Тогда полный дифференциал  функции имеет вид:
функции имеет вид:
 .
.
б) Вторую частную производную  (или кратко
(или кратко  ) находим как первую частную производную по аргументу
) находим как первую частную производную по аргументу  от функции
от функции  :
:

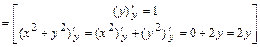
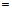
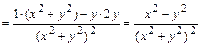 .
.
Ответ: а)  , б)
, б) 
 ;
;
7.1 – 30. Для функции  , заданной неявно, найти частные производные
, заданной неявно, найти частные производные  и
и  .
.

Для функции  , заданной уравнением
, заданной уравнением  справедливы формулы:
справедливы формулы:  ,
,  , при условии
, при условии 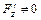 .
.
В данном примере 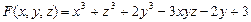 . Найдем частные производные функции
. Найдем частные производные функции  :
:
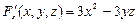 ;
;
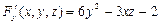 ;
;
 ;
;
Тогда, учитывая что  ,
,  , получим:
, получим:
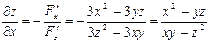 ;
;
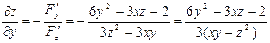
Ответ: а)  , б)
, б)  .
.
8.1 – 30. Найти локальные экстремумы функции 
 .
.
Для нахождения локальных экстремумов дифференцируемой функции  необходимо: 1) Найти область определения
необходимо: 1) Найти область определения 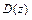 функции. 2) Найти первые частные производные
функции. 2) Найти первые частные производные  и
и  функции. 3) Решить систему уравнений (необходимое условие экстремума)
функции. 3) Решить систему уравнений (необходимое условие экстремума)  и найти точки
и найти точки  (с учётом возможных дополнительных ограничений на значения аргументов
(с учётом возможных дополнительных ограничений на значения аргументов  и
и  ) возможного локального экстремума функции. 4) Найти вторые частные производные
) возможного локального экстремума функции. 4) Найти вторые частные производные  ,
,  ,
,  ; составить выражение
; составить выражение  и вычислить значения
и вычислить значения  и
и 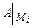 в каждой точке
в каждой точке  возможного экстремума. 5) Сделать вывод о наличии экстремумов функции
возможного экстремума. 5) Сделать вывод о наличии экстремумов функции  , используя достаточное условие экстремума: если
, используя достаточное условие экстремума: если 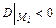 , то в точке
, то в точке  экстремума нет; если
экстремума нет; если  и
и  , то в точке
, то в точке  - локальный минимум; если
- локальный минимум; если  и
и  , то в точке
, то в точке  - локальный максимум; если
- локальный максимум; если  , то требуется дополнительное исследование точки
, то требуется дополнительное исследование точки  (например, по определению). 6) Найти локальные экстремумы (экстремальные значения) функции.
(например, по определению). 6) Найти локальные экстремумы (экстремальные значения) функции.
Решение.
1) Находим область определения функции  .
.
2) Находим первые частные производные  и
и  :
:
|
|
|

 ;
;

 .
.
3) Составим систему уравнений 



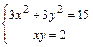 и решим её. Получим четыре решения:
и решим её. Получим четыре решения:  ,
,  ,
,  ,
,  . Из них точками возможного экстремума функции
. Из них точками возможного экстремума функции  в области
в области 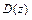 являются только две точки:
являются только две точки:  и
и  .
.
4) Находим вторые частные производные:

 ;
;

 ;
;
 ,
,
составляем выражение  и вычисляем:
и вычисляем:
 ;
;  ,
, 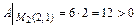 .
.
5) Делаем вывод о наличии экстремумов. Так как:
 , то в точке
, то в точке  экстремума нет;
экстремума нет;
 ,
,  , то в точке
, то в точке  - локальный минимум.
- локальный минимум.
6) Находим локальный минимум
 .
.
Ответ: 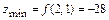 .
.
9.1–30. Найти условные экстремумы функции  приусловии
приусловии  .
.
Для нахождения методом Лагранжа локальных экстремумов дифференцируемой функции  при условии
при условии  необходимо: 1) Найти область определения
необходимо: 1) Найти область определения 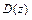 функции. 2) Составить функцию Лагранжа
функции. 2) Составить функцию Лагранжа  , где
, где  - неопределённый постоянный множитель Лагранжа. 3) Решить систему уравнений (необходимое условие условного экстремума)
- неопределённый постоянный множитель Лагранжа. 3) Решить систему уравнений (необходимое условие условного экстремума)  и найти точки
и найти точки  возможного условного локального экстремума и соответствующие им значения
возможного условного локального экстремума и соответствующие им значения  множителя Лагранжа. 4) Найти выражение второго дифференциала функции Лагранжа
множителя Лагранжа. 4) Найти выражение второго дифференциала функции Лагранжа  в точках
в точках  при условии, что
при условии, что  и
и  связаны уравнением
связаны уравнением  . 5) Сделать вывод о наличии экстремумов функции
. 5) Сделать вывод о наличии экстремумов функции  приусловии
приусловии  , используя достаточное условие условного экстремума. Если для всех
, используя достаточное условие условного экстремума. Если для всех  ,
,  (одновременно), связанных уравнением
(одновременно), связанных уравнением  ,
,  , то в точке
, то в точке  - локальный максимум; если
- локальный максимум; если  , то в точке
, то в точке  - локальный минимум. Если
- локальный минимум. Если  принимает как положительные, так и отрицательные значения, то в точке
принимает как положительные, так и отрицательные значения, то в точке  экстремума нет. 6) Найти локальные условные экстремумы функции
экстремума нет. 6) Найти локальные условные экстремумы функции  .
.
Решение.
1) Находим область определения функции  .
.
2) Составляем функцию Лагранжа:  .
.
3) Записываем необходимое условие условного экстремума  ,
,
где:  ,
,
 . Получим
. Получим 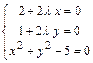 . Решая систему, находим две точки возможного условного экстремума функции
. Решая систему, находим две точки возможного условного экстремума функции  вобласти
вобласти 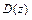 и соответствующие им значения множителя Лагранжа
и соответствующие им значения множителя Лагранжа  :
:  при
при  и
и  при
при  .
.
4) Находим выражение второго дифференциала функции Лагранжа
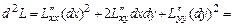


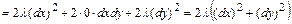 .
.
Вычисляем  при условии
при условии  , учитывая, что:
, учитывая, что:
 ;
;
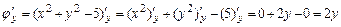 .
.
Получим:



 ;
;



 .
.
5) Делаем вывод о наличии экстремумов. Так как для всех  :
: 
 , то в точке
, то в точке  - условный локальный минимум;
- условный локальный минимум;
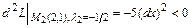 , то в точке
, то в точке  - условный локальный максимум.
- условный локальный максимум.
6) Находим условные минимум и максимум функции  при условии
при условии  :
:
 ,
, 
Ответ:  ,
,  при условии
при условии  .
.
10.1–30. Найти наибольшее и наименьшее значения функции:
 в области D:
в области D:

Функция  , дифференцируемая в ограниченной замкнутой области
, дифференцируемая в ограниченной замкнутой области 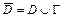 , достигает своего наибольшего и наименьшего значений или в стационарных точках
, достигает своего наибольшего и наименьшего значений или в стационарных точках  , или в точках границы
, или в точках границы  области
области 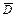 . Для их нахождения необходимо: 1) Найти все стационарные точки
. Для их нахождения необходимо: 1) Найти все стационарные точки  функции и вычислить в них значения функции
функции и вычислить в них значения функции 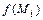 . 2) Найти наибольшее
. 2) Найти наибольшее  и наименьшее
и наименьшее  значения функции на границе
значения функции на границе  , задаваемой одним аналитическим выражением в явном виде
, задаваемой одним аналитическим выражением в явном виде  или
или  . Если
. Если  , где
, где  задаются одним аналитическим выражением в явном виде, то находят наибольшие и наименьшие значения
задаются одним аналитическим выражением в явном виде, то находят наибольшие и наименьшие значения 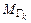 и
и  функции на каждом из участков
функции на каждом из участков  границы. 3) Сравнить значения функции
границы. 3) Сравнить значения функции 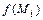 ,
, 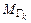 ,
,  и выбрать из них наибольшее
и выбрать из них наибольшее  и наименьшее
и наименьшее  значения функции в области
значения функции в области 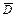 .
.
Решение. Изображаемобласть 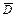 (она представляет собой треугольник, ограниченный прямыми
(она представляет собой треугольник, ограниченный прямыми  ,
,


