Законы разрушения сооружений

И ПОРАЖЕНИЯ ЛЮДЕЙ

Процесс сопротивления воздействию описывается законами разрушения и поражения. Законы разрушения характеризуют уязвимость сооружений, а законы поражения - уязвимость людей в зонах ЧС. Эти термины являются основными при прогнозировании последствий ЧС.

Под законами разрушения сооружения понимают зависимость между вероятностью его повреждения и расстоянием от эпицентра ЧС до сооружения или интенсивностью проявления поражающего фактора.

Если закон разрушения представляется в виде функции от расстояния, то закон называют координатным законом разрушения (рис. 2.2, а), а в случае зависимости от поражающего фактора параметрическим законом разрушения (рис. 2.2, б). При оценке последствий ЧС в системе гражданской обороны наибольшее распространение получили параметрические законы разрушения.

 

 

Рис. 2.2. Координатный (а) и параметрический (б) законы разрушения (поражения)

Р - вероятность; R - расстояние от центра очага до объекта;

Ф - интенсивность поражающего фактора

 

Законы разрушения сооружений

 

Законы разрушения сооружений получают на основе анализа и обобщения статистических материалов по разрушению жилых, общественных и промышленных зданий от воздействий поража­ющих факторов.

Находят применение законы разрушения двух типов: вероят­ности наступления не менее определенной степени разрушения (повреждения) сооружений – Р_Ai(Ф); и вероятности наступления определённой степени разрушения (повреждения) сооружений –Р_Bi(Ф) (рис.2.3 а, б). Для построения кривой, аппроксимирующей вероятности наступления не менее определённой степени "разру­шения (повреждения) сооружений, обычно используется нормаль­ный закон. При этом учитывается, что для одного и того же со­оружения может рассматриваться не одна, а несколько степеней разрушения.

 

 

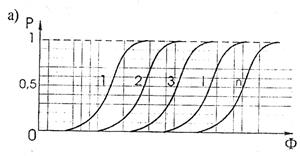
Рис. 2.3. Законы разрушения сооружений

а - вероятность возникновения не менее определённых степеней

разрушения сооружений; б - вероятность возникновения определённых

степеней разрушения сооружений; 1,2,..., i-ая степени разрушения (повреждения) сооружения;

n - число степеней разрушения

Вычисление значений вероятностей Рд,(Ф) производится по формуле нормального закона:

(2.3)

где: Ф - заданное значение случайной величины;

!Ф- переменная интегрирования случайной величины;

п = 3,14;

Мi, Oj - математическое ожидание и среднее квадратическое отклонение случайной величины для i-ой степени разрушения сооружений, определяемые на основании статистической обработки результатов экспериментов и натурных данных или рассчётным путем.

При определении вероятности наступления определенной степени разрушения (повреждения) сооружений учитывают теорию. о полной группе событий:

(2.4)

где: m - число рассматриваемых событий.

Учитывается, что после воздействия поражающего фактора сооружение может быть отнесено к одному из m несовместимых событий окаазаться целым (событие Во), получить 1,2,..., i-ю степень разрушения (В1, В2,...,Вi). Вероятности наступления определенной степени разрушения (повреждения) зданий могут быть определены непосредственно из следующих зависимостей:

где: 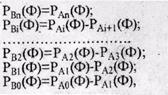(2.5)

Рм(Ф), Рл2(Ф). • • • > РА1+1(ф)" вероятности наступления не -нее 1,2,'..., i, i+1 степени разрушения (повреждения) сооружений.

В настоящее время законы разрушения получены для защитных со­жжений и зданий различных типов на воздействие ядерных взрывов воздействие взрывов техногенного характера, а также для зда-ш различной сейсмостойкости на воздействие землетрясения.

 

Законы пражения людей

Под законом поражения людей понимается зависимость вероят­ности поражения людей от интенсивности поражающего фактора.

Параметрические законы поражения людей, размещенных в зда­ниях, получены на основании экспериментальных данных, подтвер­ждающих теорему полной вероятности. В расчетах учитывается, что событие Cj (общие, безвозвратные, санитарные потери) может произойти при' получении сооружением одной из степеней повреж­дения (при одной из гипотез В,), образующих полную группу несов­местимых событий. Расчеты проводятся по формуле:

(2.6)

где: Рj(Ф) - вероятность j-гo поражения людей от воздействия поражающего фактора Ф;

Рвi(Ф) - вероятность наступления i-й степени повреждения сооружения при заданном значении поражающего фактора (закон разрушения);

вероятность получения людьми j-ой степени поражения при условии того, что наступила i-я степень повреждения здания;

n - рассматриваемое число степеней повреждения здания.

Значения получают на основе обработки материалов о последствиях авариях и стихийных бедствий.

Рис. 2.4. Законы поражения защищенного населения:

I - общие потери; 2 --безвозвратные потери; Р, - давление во фронте

ВУВ; 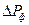расч - расчетное значение давления во фронте ВУВ

Аналогичные законы поражения получены | людей, разме­щенных в защитных сооружениях, зданиях, под. Дающихся сейс­мическому воздействию от землетрясения, а также на случай хи­мических и радиационных аварий.

 

 

2.1.4. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ОБЪЕМОВ РАЗРУШЕНИЙ И ПОРАЖЕНИЯ ЛЮДЕЙ

Задача по прогнозированию последствий крупных аварий и ка­тастроф в больших населенных пунктах решается следующим образом.

Город (населенный пункт) разбивается на элементарные пло­щадки, а их координаты представляются точками, расположен­ными в центрах площадок. Шаг сетки назначается в зависимости от точки расчета.

Точность расчета определяется следующим образом. Прогно­зируются потери населения при первой подготовке исходных дан­ных. Затем число элементарных площадок увеличивают и произ­водят повторное вычисление. Если выполняется условие:

(2.7)

то вычисление заканчивают. В формуле 2.7 приняты обозначения: Д - погрешность расчетов;

M](N), M2(N) - математическое ожидание потерь населе­ния соответственно при первом и втором расчетах; [б] - допускаемая погрешность.

Для каждой площадки подготавливаются исходные данные, вклю­чающие: характеристику застройки; численность людей.

Задача по определению последствий в малых населенных пун­ктах региона решается аналогично. При этом населенный пункт в целом может рассматривается в виде одной элементарной пло­щадки, а ее координаты представляются точкой в центре насе­ленного пункта.

Начало координат расчетной схемы выбирается произвольно на плане или принимается в системе координат карты, на кото­рой показан регион.

При прогнозировании обычно определяют математические ожи­дания показателей, характеризующие повреждения и поражения в очаге аварии или катастрофы. Такими показателями являются:

- количество зданий, получивших ту или иную степень повреждения;

- объем завалов;

- численность пострадавших.

 

Математическое ожидание числа разрушенных зданий

При прогнозировании могут встретиться два расчетных случая:

1 - если интенсивность и координаты места аварии или катас­
трофы заблаговременно заданы;

2 - когда воздействие рассматривается в виде вероятностной модели.
При заданном значении поражающего фактора Ф3 (для 1-го

расчетного случая) эта задача решается следующим образом. Принимается, что в пределах рассматриваемой площадки зда­ния размещаются с плотностью ф(х, у) (количество зданий, при­ходящихся на единицу площадки с координатами (х. у)). Тогда количество зданий в пределах площадки составит:

V(x, у) = ф(х, у) * х* у, где: х, у - размеры площадки.

Математическое ожидание числа зданий, получивших степень повреждения d в пределах площадки при заданной интенсивнос­ти поражающего фактора, будет равно:

M[Vd(x, у)] - Pd(0>5)-ф (х, у). х- у, (2.8)

где: Рd(Ф3) - вероятность получения зданиями степени повреж­дения d при интенсивности поражающего фактора(Ф3). Вероят­ность Ра(Ф3) определяется из законов разрушения.

Суммируя число поврежденных зданий по каждой площадке и переходя к пределу, получим математическое ожидание числа зданий со степенью повреждения d в пределах всего города:

M(Vd)= JJPd(O3)-p(x,y)dxdy. (2.9)

где: S_r - площадь города.

При вероятностной модели воздействия (случай 2) весь возможный диапазон интенсивности воздействия поражающего фак­тора делится на интервалы dФ. Затем для каждого интервала решается задача с учётом одновременного наступления двух событий: события, состоящего в том, что здания получат сте­пень повреждения d при значении поражающего фактора из этого интервала, и события, заключающегося в том, что в пределах рассматриваемой площадки города будет действовать поража­ющий фактор с интенсивностью из рассматриваемого интерва­ла. Вероятность одновременного наступления двух событий равна:

Рd(Ф3) = P'd (Ф3) f(x> У>ф з)* Ф, (2.10)

где: Р* (Ф3) - вероятность получения зданиями степени повреж­дения d при заданной интенсивности поражающего фактора Ф3;

f(x, у, Ф3) значение функции плотности распределения при интенсивности поражающего фактора Ф3;

f(x. у, Ф3) DФ - величина, определяющая вероятность того, что интенсивность поражающего фактора Будет находиться в пределах интервала DФ.

Вероятность получения зданиями степени повреждения d в пределах рассматриваемой площадки, с учетом возможного воздействия поражающего фактора различной интенсивности, будет зна:

(2.11)

где: Фmjn,Фmax соответственно, минимально и максимально возможное значение поражающего фактора для рассматриваемой ЧС.

Математическое ожидание числа зданий со степенью повреждения пределах площадки с координатами (х, у) при вероятностной модели воздействия определяется по формуле:

Суммируя математическое ожидание числа поврежденных зданий по каждой площадке и переходя к пределу, получим математическое ожидание повреждённых зданий со степенью d в целом городу:

Если населенный пункт небольших размеров, то его можно рассматривать как одну площадку.

Математическое ожидание объёма завалов

Объем завалов в после аварии, катастрофы или другой ЧС является основным показателем, влияющим на масштабность спасательных работ.

Кратко рассмотрим методику определения объема завалов. Пусть определенный тип застройки в пределах рассматриваемой площадки размещается с плотностью застройки в относительных единицах S(x,y). Такую информацию можно взять с карт или плана. Тогда площадь, непосредственно занятая строениями (площадь застройки), для площадки с координатами Y составит:

 

(2.14)

а объем застройки можно определить из выражения:

(2.15)

где: Н(х5 у) -- средняя высота зданий рассматриваемой площадки.

Анализ натурной информации по характеру разрушения застройки в населенных пунктах показал, что при полном разрушении (п-я степень разрушения) здания практически полностью превращаются в обломки, образуя завалы в виде обелисков. При разрушении зданий на ступень ниже полной (n-1-я степень разрушения) в расчетах можно при-пять, что объемы завалов составляют примерно 50% от объемов зава­лов в случае полного разрушения зданий. Тогда объёмы завалов в пре­делах элементарной площадки, при заданном значении поражающего фактора (расчетный случай 1), можно вычислить по формуле:

где:

вероятности получения зданиями n-i и п

степени разрушения при воздействии поражающего фактора ин­тенсивностью Ф-i, определяемые из законов разрушения;

у (х, у) - доля завала в 1 \г строительного объема зданий, характерных для площадок (удельный объем завала).

Для ориентировочных расчетов удельный объем завала можно принять: для промышленных зданий у=02: для жилых зданий у=0,4.

Суммируя объемы завалов по каждой площадке и переходя к пределу, получим объем завалов в пределах всего населенного пункта при заданной интенсивности землетрясения:

Если информация по строительному объему зданий в пределах j-ой площадки известна (например, по данным бюро технической инвентаризации), то объём завалов в пределах элементарной площадки будет равен:

где: Q(x, у) - строительный объем зданий в пределах j-ой пло­щадки с координатами х, у.

Объем завалов в пределах всего населённого пункта в этом случае определяется по формуле:

где: - кол-во элементарных площадок в пределах насел, пункта.

 

Если воздействие поражающего фактора рассматривается в де вероятностной модели (расчетный случай 2), то математическое ожидание объема завала в пределах элементарной пло-1дки определяется по формуле:

Объем завалов в пределах всего города в этом случае рассчи­тается по формуле:

Когда строительные объемы зданий в пределах j-x площадок известны (2.15), объемы завалов в пределах этих площадок при вероятностной модели воздействия вычисляются по формуле:

Объем завалов в пределах всего населённого пункта в этом случае разделяется суммированием (2.19).

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: