 |
Числовые характеристики непрерывных случайных величин
|
|
|
|
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ox, определяется равенством
,
где f (x) – плотность распределения случайной величины X. Предполагается, что интеграл сходится абсолютно.
В частности, если все возможные значения принадлежат интервалу
(а, b), то
.
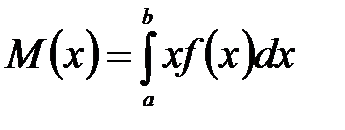Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох, определяется равенством
,
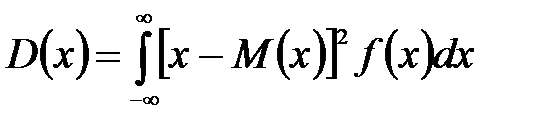или равносильным равенством
.
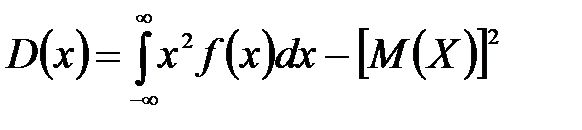В частности, если все возможные значения X принадлежат интервалу (a, b), то
.
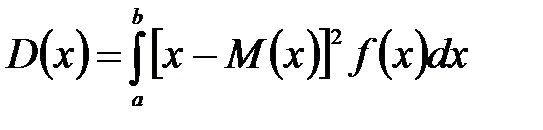Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины:
.
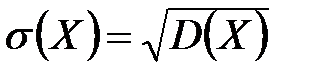Нормальный закон распределения
Нормальным называют распределение вероятностей случайной величины X, плотность которого имеет вид
,
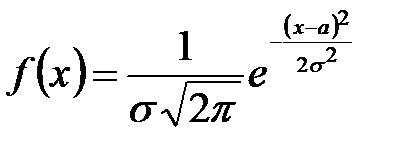где а – математическое ожидание,
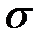– среднее квадратическое отклонение X.
Вероятность того, что нормально распределенная случайная величина X примет значение, принадлежащее интервалу (α; β), равна:
,
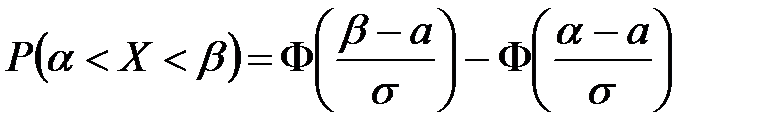где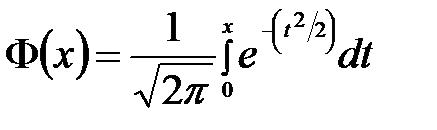 
– функция Лапласа.
Генеральная совокупность и выборка
Генеральная совокупность – вся подлежащая изучению совокупность наблюдений, производимых в неизменных условиях.
В математической статистике генеральная совокупность часто понимается как совокупность всех мыслимых наблюдений, которые могут быть произведены при выполнении некоторых условий.
Выборка (выборочная совокупность) – совокупность наблюдений, отобранных случайным образом из генеральной совокупности.
Число наблюдений в совокупности называется ее объемом.
N – объем генеральной совокупности.
n – объем выборки.
Вариационный ряд
|
|
|
Наблюдаемые значения случайной величины х 1, х 2, …, хk называются вариантами.
Частотой варианты х i называется число ni (i =1,…, k), показывающее, сколько раз эта варианта встречается в выборке.
Частостью (относительной частотой, долей) варианты хi (i =1,…, k) называется отношение ее частоты ni к объему выборки n.
Частоты и частости называют весами.
Накопленной частотой называется количество вариант, значения которых меньше данного х:
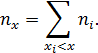
Накопленной частостью называется отношение накопленной частоты к объему выборки:
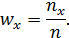
Вариационным рядом (статистическим рядом) – называется последовательность вариант, записанных в порядке возрастания и соответствующих им весов.
Вариационный ряд может быть дискретным (выборка значений дискретной случайной величины) и непрерывным (интервальным) (выборка значений непрерывной случайной величины).
Дискретный вариационный ряд имеет вид:
| 
| 
| … | 
|
| 
| 
| … | 
|
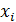
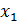
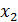
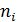
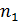
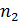
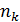
Когда число вариант велико или признак является непрерывным (случайная величина может принимать любые значения в некотором интервале), составляют интервальный вариационный ряд.
Для построения интервального вариационного ряда проводят группировку вариант – их разбивают на отдельные интервалы:
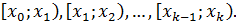
Число интервалов иногда определяют с помощью формулы Стерджеса:
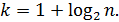
Затем подсчитывается число вариант, попавших в каждый интервал – частоты ni (или частости ni / n). Если варианта находится на границе интервала, то ее присоединяют к правому интервалу.
Интервальный вариационный ряд имеет вид:
| Варианты |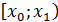 
| 
| … | 
|
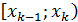
| Частоты |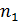
|
| … |
|
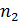
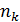
Эмпирической (статистической) функцией распределения называется функция, значение которой в точке х равно относительной частоте того, что варианта примет значение, меньшее х (накопительной частости для х):
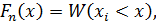
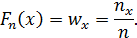
Полигоном частот называют ломанную, отрезки которой соединяют точки с координатами (х 1; n 1), (х 2; n 2), …, (хk; nk). Аналогично строится полигон частостей, который является статистическим аналогом многоугольника распределений.
|
|
|
Для непрерывного вариационного ряда полигон можно построить, если в качестве значений х 1, х 2, …, хk взять середины интервалов.
Интервальный вариационный ряд графически обычно изображают с помощью гистограммы.
Гистограмма – ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длины h = xi +1 – xi, i = 0,…, k -1, а высоты равны частотам (или частостям) интервалов ni (wi).
Кумулята (кумулятивная кривая) – кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломанную, соединяющую точк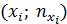и 
или 
, 
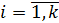. Для интервального ряда кумулята начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте (частости), равной нулю. Другие точки этой ломанной соответствуют концам интервалов.
|
|
|
