 |
Теоремы сложения и умножения вероятностей
|
|
|
|
Варианты 1-10 (N – номер варианта)
В урне N белых и (25 – N) черных шаров. Из урны последовательно достают два шара. Найти вероятность того, что:
1) шары будут разных цветов, если шары возвращают в урну;
2) шары будут одинакового цвета, если шары не возвращают в урну;
3) хотя бы один шар будет белым, если шары не возвращают в урну.
Варианты 11-20 (N – номер варианта)
В урне (N – 6 ) белых и (31 – N) черных шаров. Из урны последовательно достают все шары. Найти вероятность того, что
1) третьим по порядку будет вынут белый шар;
2) из первых трех шаров хотя бы один будет белым шаром.
Варианты 21-30 (N – номер варианта)
В урне (N – 16 ) белых и 5 черных шаров и (36 – N) красных шаров. Три из них вынимаются наугад. Найти вероятность того, что по крайней мере два из них будут разноцветными при условии: а) шары возвращаются в урну; б) шары не возвращаются в урну.
Формула полной вероятности. Формула Байеса
Варианты 1-10 (N – номер варианта)
Имеются три одинаковые с виду урны. В первой N белых шаров и
(25 – N) черных шаров; во второй урне (20 – N) белых и (N + 5) черных; в третьей только белые шары. Из наугад выбранной урны достают один шар. Какова вероятность, что этот шар белый?
Варианты 11-20 (N – номер варианта)
Имеются две урны: в первой (N – 5) белых шаров и (30 – N) черных шаров; во второй урне (21 – N) белых и (N + 4) черных. Из первой урны во вторую перекладывают, не глядя, один шар. После этого из второй урны достают один шар. Найти вероятность того, что этот шар будет белым.
Варианты 21-30 (N – номер варианта)
Имеются три урны: в первой (N – 15) белых шаров и (35 – N) черных шаров; во второй урне (40 – N) белых и (N – 20) черных; в третьей – N белых шаров (черных нет). Из наугад выбранной урны достали один шар. Этот шар оказался белым. Найти вероятность того, что шар достали из первой урны.
|
|
|
Формула Бернулли
Варианты 1-10 (N – номер варианта)
В семье 6 детей. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди этих детей:
N = 1) один мальчик;
N = 2) более одного мальчика;
N = 3) два мальчика;
N = 4) более двух мальчиков;
N = 5) не более двух мальчиков;
N = 6) три мальчика;
N = 7) более трех мальчиков;
N = 8) не более трех мальчиков;
N = 9) четыре мальчика;
N = 10) не более четырех мальчиков.
Варианты 11-20 (N – номер варианта)
Отрезок АВ разделен точкой С в отношении 3:1. На этот отрезок наудачу брошено шесть точек. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. Найти вероятность того, что:
N = 11) одна точка окажется левее точки С;
N = 12) более одной точки окажется левее точки С;
N = 13) две точки окажется левее точки С;
N = 14) более двух точек окажется левее точки С;
N = 15) не более двух точек окажется левее точки С;
N = 16) три точки окажется левее точки С;
N = 17) более трех точек окажется левее точки С;
N = 18) не более трех точек окажется левее точки С;
N = 19) четыре точки окажется левее точки С;
N = 20) не более четырех точек окажется левее точки С.
Варианты 21-30 (N – номер варианта)
Монету бросают 6 раз. Найти вероятность того, что «герб» выпадет:
N = 21) один раз;
N = 22) более одного раза;
N = 23) два раза;
N = 24) более двух раз;
N = 25) не более двух раз;
N = 26) три раза;
N = 27) более трех раз;
N = 28) не более трех раз;
N = 29) четыре раза;
N = 30) не более четырех раз.
Локальная и интегральная теоремы Муавра-Лапласа. Формула Пуассона
Варианты 1-10 (N – номер варианта)
Найти вероятность того, что событие А наступит ровно (70 + N) раз в (250 + N) независимых испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Варианты 11-20 (N – номер варианта)
|
|
|
Вероятность появления события А в каждом из (120 + N) независимых постоянна и равна 0,8. Найти вероятность того, что событие А появится не менее (70 + N) раз.
Варианты 21-30 (N – номер варианта)
Проведено (10 × N) независимых испытаний с вероятностью появления события А в каждом из них (N /1000). Найти вероятность того, что событие А появится точно 2 раза.
Дискретные случайные величины
В денежной лотерее выпущено 1000 билетов. Разыгрывается a 1 выигрышей на сумму p 1 тысяч рублей, a 2 выигрышей на сумму p 2 тысяч рублей и a 3 выигрышей на сумму p 3 тысяч рублей. Составить ряд распределения случайной величины Х – размер выигрыша по одному купленному билету; найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины; записать функцию распределения и построить ее график.
Варианты (N – номер варианта)
| N | a 1 | p 1 | a 2 | p 2 | a 3 | p 3 | N | a 1 | p 1 | a 2 | p 2 | a 3 | p 3 |
| 1. | 2. | ||||||||||||
| 3. | 4. | ||||||||||||
| 5. | 6. | ||||||||||||
| 7. | 8. | ||||||||||||
| 9. | 10. | ||||||||||||
| 11. | 12. | ||||||||||||
| 13. | 14. | ||||||||||||
| 15. | 16. | ||||||||||||
| 17. | 18. | ||||||||||||
| 19. | 20. | ||||||||||||
| 21. | 22. | ||||||||||||
| 23. | 24. | ||||||||||||
| 25. | 26. | ||||||||||||
| 27. | 28. | ||||||||||||
| 29. | 30. |
Нормальный закон распределения
Пусть Х – нормально распределенная случайная величина с математическим ожиданием а и средним квадратическим отклонением s. Найдите вероятность того, что Х примет значение между a и b.
| N | a | s | a | b | N | a | s | a | b | N | a | s | a | b |
| 1. | 2. | 3. | ||||||||||||
| 4. | 5. | 6. | ||||||||||||
| 7. | 8. | 9. | ||||||||||||
| 10. | 11. | 12. | ||||||||||||
| 13. | 14. | 15. | ||||||||||||
| 16. | 17. | 18. | ||||||||||||
| 19. | 20. | 21. | ||||||||||||
| 22. | 23. | 24. | ||||||||||||
| 25. | 26. | 27. | ||||||||||||
| 28. | 29. | 30. |
|
|
|
Вариационный ряд
Дана выборка значений некоторого непрерывного количественного признака Х, объем выборки n = 50 (см. значения по вариантам в таблице ниже).
Требуется:
1) Построить интервальный ряд, определив количество интервалов по формуле Стерджеса, рассчитать частоты, относительные частоты (частости), накопленные частоты, накопленные частости.
2) Построить гистограмму, кумуляту.
3) Найти средние величины: выборочное среднее, медиану, моду.
4) Найти показатели вариации: размах, среднее линейное отклонение, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение, коэффициент вариации.
| Вар | Вар 2 | Вар 3 | Вар 4 | Вар 5 | Вар 6 | Вар 7 | Вар 8 | Вар 9 | Вар 10 | Вар 11 | Вар 12 | Вар 13 | Вар 14 | Вар 15 |
| 3,92 | 2,84 | -1,09 | 4,38 | 1,76 | 10,53 | 5,65 | 9,72 | 6,08 | 12,47 | 10,17 | 10,23 | 13,49 | 12,25 | 14,04 |
| 3,32 | 0,69 | 2,81 | 1,52 | 1,68 | 1,77 | 6,81 | 11,68 | 7,02 | 12,13 | 9,95 | 12,25 | 12,01 | 14,41 | 19,12 |
| -0,22 | 2,72 | 5,66 | 7,06 | 7,66 | 8,36 | 11,91 | 7,57 | 12,82 | 13,52 | 9,22 | 12,10 | 13,62 | 12,13 | 14,04 |
| 1,70 | 0,54 | 3,56 | 3,70 | 7,49 | 7,18 | 4,42 | 6,28 | 7,73 | 13,74 | 10,40 | 10,40 | 14,12 | 13,34 | 14,93 |
| 1,37 | 6,54 | 4,78 | 4,69 | 4,63 | 6,20 | 7,50 | 6,41 | 11,11 | 10,12 | 9,70 | 12,22 | 14,35 | 14,21 | 14,70 |
| -1,19 | 1,06 | 2,76 | 3,43 | 4,06 | 6,75 | 6,68 | 7,50 | 7,95 | 14,09 | 11,76 | 9,89 | 9,90 | 12,27 | 15,94 |
| 0,54 | 1,77 | 4,43 | 2,63 | 6,51 | 5,59 | 3,56 | 8,91 | 12,89 | 8,09 | 12,16 | 12,24 | 11,94 | 16,92 | 15,64 |
| 4,56 | 1,49 | 4,31 | 3,62 | 5,92 | 2,35 | 10,46 | 5,69 | 8,47 | 10,90 | 10,45 | 10,48 | 11,66 | 14,52 | 14,30 |
| 3,41 | 3,69 | 4,60 | 5,71 | 5,89 | 4,55 | 5,49 | 5,43 | 11,08 | 8,27 | 10,31 | 12,24 | 12,28 | 14,47 | 13,56 |
| 2,50 | 2,05 | -0,26 | 6,66 | 5,18 | 5,77 | 5,71 | 7,08 | 9,73 | 8,79 | 6,96 | 8,39 | 14,14 | 11,81 | 14,75 |
| 0,61 | 0,83 | 3,00 | 3,66 | 1,51 | 10,96 | 7,15 | 7,28 | 8,18 | 9,68 | 9,05 | 9,93 | 12,09 | 15,68 | 15,19 |
| -0,92 | 4,43 | 3,76 | 2,06 | 6,85 | 4,92 | 6,81 | 5,98 | 11,63 | 8,92 | 10,28 | 13,01 | 14,91 | 16,86 | 17,99 |
| 0,74 | -3,05 | 3,45 | 1,33 | 4,04 | 6,37 | 6,05 | 7,75 | 6,44 | 10,10 | 11,24 | 8,67 | 14,35 | 15,02 | 16,40 |
| 2,47 | 0,60 | 3,15 | 3,08 | 5,73 | 8,39 | 7,73 | 9,84 | 10,37 | 9,56 | 9,52 | 12,49 | 15,51 | 8,29 | 16,67 |
| 2,08 | 6,43 | 1,15 | 7,80 | 6,60 | 9,10 | 11,38 | 8,35 | 11,16 | 10,54 | 9,41 | 14,66 | 13,54 | 14,35 | 18,76 |
| 1,41 | 0,58 | -1,15 | 3,52 | 7,23 | 0,75 | 7,05 | 7,40 | 8,96 | 7,86 | 10,19 | 10,38 | 16,04 | 15,99 | 15,35 |
| -0,28 | 6,20 | -0,99 | 2,62 | 7,43 | 1,73 | 5,51 | 7,03 | 10,58 | 9,98 | 12,23 | 13,52 | 12,07 | 12,99 | 18,45 |
| 2,01 | 4,13 | 1,79 | 7,37 | 2,65 | 4,07 | 9,28 | 6,72 | 10,07 | 7,73 | 12,13 | 12,83 | 11,68 | 18,42 | 12,66 |
| 0,02 | 2,55 | 4,14 | 4,94 | 7,09 | 4,57 | 2,91 | 5,89 | 12,53 | 12,47 | 10,46 | 13,35 | 10,10 | 13,79 | 14,87 |
| -0,60 | 3,02 | 2,39 | 5,74 | 8,19 | 7,14 | 6,37 | 11,49 | 8,74 | 12,76 | 12,16 | 10,55 | 13,48 | 15,35 | 17,55 |
| -0,23 | 2,12 | 1,17 | 3,55 | 5,37 | 9,23 | 5,85 | 8,96 | 10,73 | 10,19 | 10,53 | 9,25 | 10,12 | 14,16 | 15,75 |
| -0,24 | 4,99 | 3,27 | 3,71 | 2,94 | 6,27 | 2,99 | 9,66 | 13,11 | 8,05 | 11,48 | 11,66 | 10,11 | 13,37 | 14,69 |
| 3,96 | -1,67 | 1,21 | 6,76 | 9,25 | 5,67 | 8,59 | 9,42 | 6,56 | 10,35 | 7,60 | 13,63 | 13,21 | 12,95 | 12,98 |
| 4,24 | 0,30 | 2,19 | 9,13 | 4,56 | 5,36 | 11,27 | 11,54 | 6,22 | 11,16 | 13,23 | 13,14 | 15,48 | 14,38 | 15,65 |
| 0,62 | 1,70 | 1,76 | 1,99 | 8,41 | 4,67 | 4,47 | 8,27 | 9,53 | 6,07 | 12,31 | 13,49 | 13,76 | 16,09 | 12,59 |
| -0,17 | 2,48 | 0,75 | 2,94 | 5,02 | 7,01 | 7,42 | 6,90 | 9,72 | 11,59 | 14,87 | 9,59 | 11,75 | 13,96 | 12,84 |
| 2,30 | 3,14 | 3,78 | -0,03 | 6,75 | 3,89 | 5,50 | 9,61 | 8,89 | 7,71 | 11,15 | 9,57 | 12,00 | 13,15 | 15,19 |
| -1,26 | 1,62 | 1,25 | 5,85 | 2,51 | 9,38 | 8,39 | 10,63 | 8,25 | 11,37 | 9,10 | 14,29 | 12,06 | 13,94 | 15,53 |
| 1,43 | -0,37 | 2,87 | 5,41 | 7,45 | 2,89 | 4,81 | 11,79 | 8,48 | 12,28 | 11,91 | 11,02 | 15,64 | 14,34 | 12,11 |
| -2,44 | 5,94 | 4,74 | 4,80 | 1,91 | 6,28 | 7,08 | 6,93 | 7,62 | 8,26 | 9,89 | 11,31 | 14,16 | 13,95 | 16,73 |
| 1,83 | 4,51 | 0,54 | 2,21 | 7,18 | 8,60 | 3,33 | 11,83 | 7,78 | 10,68 | 10,03 | 16,39 | 14,41 | 13,64 | 13,57 |
| 3,88 | 0,47 | 1,41 | 3,68 | 4,35 | 2,15 | 6,41 | 10,14 | 8,93 | 9,03 | 10,50 | 12,61 | 10,24 | 13,43 | 14,48 |
| 6,06 | 3,63 | 3,53 | 2,07 | -0,40 | 6,78 | 7,14 | 7,21 | 8,86 | 8,02 | 13,44 | 10,61 | 13,65 | 18,03 | 11,94 |
| -2,27 | 2,01 | 3,66 | -0,29 | 4,53 | 7,79 | 5,80 | 6,70 | 9,43 | 11,40 | 15,33 | 10,74 | 12,33 | 17,04 | 15,55 |
| -3,20 | 1,40 | 3,17 | 3,27 | 4,80 | 6,74 | 8,14 | 7,68 | 9,83 | 10,69 | 8,17 | 12,62 | 14,41 | 18,11 | 17,44 |
| 0,59 | 1,48 | 3,92 | 1,73 | 5,25 | 5,63 | 5,56 | 8,13 | 10,91 | 8,72 | 16,94 | 11,94 | 9,87 | 12,96 | 12,96 |
| 1,88 | 4,04 | 4,73 | 4,25 | 7,64 | 3,33 | 11,08 | 9,68 | 10,04 | 9,19 | 8,49 | 16,81 | 11,99 | 16,07 | 19,11 |
| 4,62 | -0,12 | 5,08 | 2,55 | 4,29 | 3,20 | 8,78 | 8,53 | 10,42 | 10,10 | 9,80 | 15,07 | 15,84 | 14,22 | 14,12 |
| -0,63 | 1,63 | 3,41 | 3,50 | 6,21 | 6,57 | 7,98 | 5,07 | 9,93 | 9,07 | 11,15 | 14,72 | 10,68 | 13,05 | 13,38 |
| 2,70 | 0,48 | 4,95 | 4,19 | 1,41 | 6,86 | 8,17 | 6,62 | 10,51 | 10,58 | 9,84 | 11,94 | 12,99 | 13,07 | 11,43 |
| 0,69 | 4,41 | 0,78 | 5,84 | 5,46 | 6,48 | 8,62 | 9,84 | 12,01 | 7,21 | 11,35 | 15,18 | 13,52 | 12,13 | 17,60 |
| 1,57 | 0,91 | 2,24 | 4,28 | 7,25 | 8,80 | 4,75 | 10,11 | 9,64 | 11,71 | 10,02 | 11,94 | 13,66 | 9,11 | 15,18 |
| 0,06 | 3,09 | 6,96 | 1,44 | 5,13 | 9,49 | 8,54 | 9,75 | 4,97 | 8,80 | 7,54 | 10,71 | 15,90 | 16,01 | 15,54 |
| 1,41 | 2,50 | 5,66 | 2,48 | 5,59 | 4,75 | 6,46 | 6,70 | 13,37 | 9,71 | 8,67 | 13,59 | 11,34 | 12,87 | 10,61 |
| 3,93 | 4,58 | 1,66 | 0,96 | 2,34 | 4,23 | 8,04 | 4,93 | 8,71 | 8,52 | 8,95 | 7,62 | 12,89 | 15,55 | 17,05 |
| -1,17 | 1,62 | 3,79 | 8,06 | 3,17 | 2,11 | 6,29 | 7,61 | 6,70 | 9,48 | 11,04 | 11,56 | 18,01 | 12,99 | 17,84 |
| 0,00 | 5,89 | 0,50 | 2,48 | 5,44 | 7,84 | 4,10 | 9,94 | 6,85 | 10,38 | 12,80 | 15,52 | 16,96 | 15,23 | 13,65 |
| -0,56 | 0,68 | 2,57 | 1,65 | 3,24 | 6,73 | 3,59 | 6,40 | 10,25 | 10,88 | 8,66 | 12,69 | 11,87 | 15,92 | 13,85 |
| -0,09 | 0,78 | -0,04 | 2,69 | 7,67 | 6,73 | 7,97 | 7,89 | 4,43 | 3,92 | 14,67 | 12,05 | 13,20 | 15,70 | 15,60 |
| 5,10 | 0,29 | 1,08 | 5,10 | 5,87 | 5,96 | 10,40 | 6,77 | 9,36 | 8,19 | 9,98 | 9,72 | 15,28 | 13,58 | 14,45 |
|
|
|
| Вар | Вар 17 | Вар 18 | Вар 19 | Вар 20 | Вар 21 | Вар 22 | Вар 23 | Вар 24 | Вар 25 | Вар 26 | Вар 27 | Вар 28 | Вар 29 | Вар 30 |
| 1,35 | 3,73 | 4,89 | 4,44 | 6,49 | 2,88 | 3,09 | 2,12 | 15,30 | 5,95 | 13,01 | 12,75 | 14,08 | 16,80 | 14,73 |
| -2,43 | 3,37 | -0,41 | 3,01 | 7,61 | 6,83 | 7,28 | 5,59 | 12,76 | 6,12 | 13,26 | 11,23 | 11,02 | 15,16 | 13,65 |
| 4,61 | 5,10 | 1,89 | 9,32 | 12,68 | 9,24 | 6,55 | 9,74 | 10,70 | 10,13 | 10,65 | 12,06 | 16,74 | 16,34 | 15,72 |
| 2,08 | 2,25 | 5,45 | 4,59 | 8,85 | 1,74 | 4,89 | 13,34 | 6,32 | 10,78 | 11,90 | 10,38 | 9,14 | 13,48 | 11,29 |
| -1,45 | 0,69 | 3,75 | 5,01 | -1,15 | 5,45 | 4,77 | 8,21 | 10,29 | 12,07 | 11,71 | 9,16 | 16,93 | 11,91 | 14,63 |
| 2,91 | 1,95 | 6,59 | -0,98 | 10,10 | 2,68 | 9,77 | 9,13 | 15,66 | 8,02 | 11,20 | 12,58 | 11,84 | 12,99 | 17,16 |
| 3,28 | 2,11 | 1,02 | 5,60 | 3,86 | 11,05 | 8,76 | 6,03 | 12,94 | 13,00 | 14,07 | 12,10 | 13,34 | 12,43 | 13,55 |
| -0,67 | 5,69 | 7,99 | 4,68 | 7,46 | 6,46 | 6,57 | 10,53 | 9,09 | 9,82 | 15,58 | 16,73 | 13,20 | 10,16 | 11,74 |
| 3,73 | -2,86 | 2,79 | 1,40 | 3,90 | 5,09 | 3,55 | 9,90 | 5,03 | 14,58 | 13,51 | 10,93 | 16,97 | 17,10 | 19,09 |
| 2,36 | 0,95 | 2,75 | 5,19 | 1,77 | 11,82 | 8,75 | 9,24 | 6,28 | 8,34 | 10,67 | 9,76 | 10,37 | 16,82 | 13,69 |
| -0,50 | 2,43 | -0,18 | 6,37 | 4,66 | 6,84 | 13,08 | 11,43 | 11,85 | 4,50 | 9,82 | 7,20 | 11,94 | 15,68 | 18,74 |
| 2,46 | 2,38 | 4,05 | 3,02 | 7,31 | 3,84 | 8,45 | 5,75 | 8,41 | 13,45 | 13,42 | 11,36 | 12,23 | 15,16 | 11,66 |
| 1,46 | 1,87 | 3,39 | 4,77 | 6,76 | 9,84 | 9,27 | 10,94 | 10,68 | 7,32 | 10,90 | 16,66 | 11,29 | 13,39 | 8,96 |
| 4,42 | 2,29 | 0,82 | 5,15 | 4,99 | 4,85 | 6,17 | 8,42 | 5,52 | 6,13 | 12,56 | 13,18 | 10,38 | 15,93 | 18,67 |
| 3,08 | 2,32 | 3,83 | 5,44 | 7,59 | 12,52 | 10,03 | 8,64 | 4,65 | 8,06 | 11,22 | 15,05 | 13,95 | 11,94 | 11,49 |
| -0,77 | 0,78 | 3,97 | 3,26 | 1,52 | 7,36 | 4,67 | 12,80 | 5,09 | 8,27 | 5,39 | 9,48 | 15,70 | 16,16 | 11,20 |
| 3,79 | -3,26 | 2,34 | 1,46 | 4,78 | 7,19 | 6,89 | -0,06 | 9,98 | 10,88 | 14,53 | 7,21 | 12,33 | 12,25 | 11,12 |
| 0,90 | 2,40 | 0,70 | 1,33 | 10,70 | 6,70 | 4,88 | 7,68 | 4,37 | 6,98 | 13,13 | 7,70 | 14,48 | 13,94 | 18,64 |
| -1,72 | -5,55 | 4,85 | 7,93 | -0,93 | 6,62 | 8,07 | 8,51 | 10,48 | 6,90 | 14,08 | 13,76 | 12,59 | 11,19 | 18,90 |
| 3,37 | 3,86 | 3,64 | 6,22 | 1,74 | 5,32 | 13,40 | 6,09 | 8,81 | 6,11 | 14,00 | 14,22 | 13,55 | 17,61 | 10,29 |
| -1,83 | 2,83 | 5,83 | 3,25 | 6,38 | 5,32 | 4,68 | 6,39 | 7,13 | 10,99 | 9,21 | 15,06 | 4,44 | 16,89 | 14,39 |
| -2,53 | 1,13 | 1,74 | 3,65 | 7,67 | 8,66 | 7,09 | 10,02 | 8,87 | 14,73 | 12,71 | 16,04 | 15,10 | 11,29 | 10,62 |
| 0,00 | 2,81 | 4,17 | -0,25 | 4,68 | 4,68 | 8,56 | 7,81 | 8,54 | 11,52 | 12,64 | 11,66 | 12,58 | 16,19 | 17,20 |
| 1,62 | 1,83 | -4,04 | 4,06 | 9,87 | 4,70 | 5,11 | 6,26 | 5,28 | 10,85 | 12,25 | 10,12 | 15,23 | 19,56 | 15,96 |
| 4,13 | -0,36 | -2,37 | 7,02 | 10,46 | 11,49 | 9,14 | 9,61 | 13,92 | 6,47 | 14,74 | 5,98 | 12,12 | 13,40 | 21,74 |
| 0,58 | 2,59 | -0,35 | 7,34 | 6,38 | 7,70 | 6,63 | 3,52 | 0,60 | 16,41 | 13,24 | 8,81 | 6,45 | 15,23 | 13,46 |
| 1,71 | 1,03 | 1,96 | 4,01 | -0,01 | 4,48 | 0,87 | 4,21 | 6,83 | 7,49 | 9,85 | 9,86 | 12,82 | 12,93 | 9,41 |
| 0,71 | -4,42 | 2,79 | 4,72 | 5,21 | 2,89 | 5,92 | 2,49 | 8,88 | 11,57 | 12,13 | 9,17 | 10,90 | 17,77 | 16,27 |
| -2,70 | 1,82 | 0,15 | 3,82 | 4,95 | 9,56 | 9,91 | 7,04 | 3,54 | 10,13 | 7,64 | 11,57 | 11,91 | 11,53 | 13,38 |
| -0,20 | 9,44 | 0,46 | 3,25 | 3,60 | 0,99 | 7,37 | 9,86 | 9,53 | 8,61 | 12,24 | 13,84 | 14,30 | 14,10 | 14,18 |
| 3,73 | -2,43 | 4,20 | 2,17 | 3,68 | 5,98 | 8,24 | 9,48 | 10,15 | 4,93 | 9,83 | 8,24 | 13,69 | 13,62 | 19,08 |
| -1,57 | 1,97 | 2,43 | 1,28 | 3,74 | 7,73 | 1,47 | 9,65 | 5,48 | 8,02 | 9,57 | 9,14 | 11,53 | 17,06 | 10,06 |
| -2,40 | -1,37 | 7,59 | -1,82 | 2,50 | 7,09 | 10,15 | 8,42 | 11,30 | 10,87 | 8,85 | 9,64 | 7,59 | 11,33 | 15,79 |
| -1,04 | 0,87 | 4,71 | 6,91 | 4,78 | 7,85 | 10,90 | 3,29 | 9,10 | 11,34 | 12,63 | 11,40 | 13,90 | 15,04 | 13,95 |
| -0,47 | -0,44 | 3,67 | 5,30 | 11,10 | 6,22 | 9,11 | 8,92 | 13,12 | 8,40 | 16,88 | 8,04 | 16,24 | 11,35 | 14,09 |
| 3,67 | 5,21 | 2,00 | -0,72 | 3,36 | 5,90 | 2,04 | 9,03 | 6,30 | 13,79 | 11,36 | 14,37 | 17,33 | 13,13 | 13,14 |
| 4,03 | 1,44 | 0,99 | 5,78 | -1,65 | 5,30 | 6,78 | 6,23 | 9,56 | 10,42 | 16,23 | 10,86 | 13,60 | 9,15 | 17,57 |
| 3,69 | -0,39 | 0,23 | 1,43 | 8,23 | 3,59 | 4,86 | 7,42 | 8,59 | 5,64 | 5,64 | 16,05 | 16,52 | 12,43 | 9,74 |
| -1,25 | 3,97 | 2,63 | 9,13 | 7,73 | 7,99 | 7,95 | 11,17 | 7,55 | 14,33 | 9,06 | 11,31 | 10,95 | 11,90 | 7,27 |
| 6,86 | 5,38 | 4,16 | 7,66 | 4,06 | 9,50 | 7,40 | 5,04 | 14,05 | 17,09 | 11,53 | 5,42 | 14,42 | 14,55 | 20,80 |
| 0,38 | 3,01 | 8,62 | 5,58 | 1,44 | 0,78 | 7,34 | 6,54 | 10,75 | 14,22 | 8,28 | 12,11 | 10,81 | 21,39 | 13,71 |
| 1,87 | 2,22 | 5,90 | 1,31 | 10,86 | 0,90 | 7,73 | 8,12 | 9,60 | 8,21 | 13,31 | 13,89 | 9,21 | 12,85 | 14,07 |
| -1,83 | 9,21 | 3,37 | 1,86 | 6,42 | 6,54 | 9,18 | 10,61 | 8,00 | 11,80 | 16,49 | 11,09 | 10,01 | 12,87 | 15,75 |
| 0,05 | 2,21 | 4,39 | 2,14 | 6,33 | 9,13 | 7,68 | 4,51 | 12,34 | 10,01 | 7,45 | 12,63 | 15,47 | 17,16 | 12,33 |
| 2,33 | 1,82 | 1,97 | 9,97 | -1,18 | 6,10 | 8,71 | 7,60 | 8,12 | 8,21 | 6,98 | 15,61 | 13,46 | 10,71 | 12,87 |
| 6,65 | 1,94 | 6,39 | 7,14 | 5,48 | 4,17 | 4,98 | 9,20 | 8,81 | 11,49 | 12,63 | 14,47 | 12,86 | 13,99 | 14,47 |
| -0,36 | 4,22 | 5,40 | 4,27 | 0,09 | 6,16 | 5,40 | -1,16 | 10,91 | 10,87 | 9,61 | 11,96 | 16,06 | 14,51 | 19,73 |
| 1,49 | 3,69 | 5,88 | 0,15 | 0,76 | 5,61 | 7,25 | 16,75 | 8,72 | 11,72 | 10,28 | 18,13 | 13,11 | 8,15 | 13,11 |
| -1,14 | 4,27 | 3,15 | 3,42 | 4,91 | 5,20 | 4,74 | 8,60 | 12,96 | 6,67 | 14,58 | 13,34 | 11,44 | 16,31 | 18,40 |
| 1,87 | 4,03 | 6,49 | 2,64 | 4,26 | 6,61 | 10,21 | 8,81 | 10,88 | 6,92 | 8,41 | 16,56 | 15,85 | 12,29 | 13,96 |
|
|
|
Список литературы
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1998. – 576 с.
2. Вентцель Е.С., Овчаров Л.А. Теория вероятностей. Задачи и упражнения. – М., Наука, 1969. – 368 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2004. - 405 с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003. - 479 с.
5. Гнеденко Б.В. Курс теории вероятностей. – М.: Едиториал УРСС, 2005. - 448 с.
6. Елисеева И.И. Теория статистики с основами теории вероятностей. – М.: ЮНИТИ-ДАНА, 2001. - 446 с.
7. Зарубин В.С., Крищенко А.П. Теория вероятностей. – М.: Изд-во МГТУ им. Баумана, 2004. - 456 с.
8. Колемаев В.А., Калинина В.Н., Соловьев В.И. и др. Теория вероятностей в примерах и задачах / Учебное пособие. – М., 2001. – 87 с.
9. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ-ДАНА, 2004. - 573 с.
10. Письменный Д. Конспект лекций по теории вероятностей и математической статистике. – М.: Айрис пресс, 2004 - 256 с.
Приложение 1
Таблица значений функции 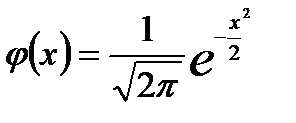
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
Приложение 2
Таблица значений функции 
| x | 
| x | 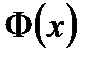
| x | 
| x | 
|
| 0,00 | 0,0000 | 0,40 | 0,1554 | 0,80 | 0,2881 | 1,20 | 0,3849 |
| 0,01 | 0,0040 | 0,41 | 0,1591 | 0,81 | 0,2910 | 1,21 | 0,3869 |
| 0,02 | 0,0080 | 0,42 | 0,1628 | 0,82 | 0,2939 | 1,22 | 0,3883 |
| 0,03 | 0,0120 | 0,43 | 0,1664 | 0,83 | 0,2967 | 1,23 | 0,3907 |
| 0,04 | 0,0160 | 0,44 | 0,1700 | 0,84 | 0,2995 | 1,24 | 0,3925 |
| 0,05 | 0,0199 | 0,45 | 0,1736 | 0,85 | 0,3023 | 1,25 | 0,3944 |
| 0,06 | 0,0239 | 0,46 | 0,1772 | 0,86 | 0,3051 | 1,26 | 0,3962 |
| 0,07 | 0,0279 | 0,47 | 0,1808 | 0,87 | 0,3078 | 1,27 | 0,3980 |
| 0,08 | 0,03
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

