 |
Формула полной вероятности. Формула Байеса
|
|
|
|
4) Имеются три одинаковые с виду урны: в первой 5 белых и 10 черных шаров; во второй 9 белых и 6 черных шаров; в третьей только черные шары. Из наугад выбранной урны достают один шар. Какова вероятность того, что этот шар черный.
Решение
Событие A – достали черный шар. Событие A может произойти с одним из несовместных событий (гипотез):
H 1 – шар достали из первой урны;
H 2 – шар достали из второй урны;
H 3 – шар достали из третьей урны.
Так как урны с виду одинаковы, то:
Найдем условные вероятности события A для каждой гипотезы.
Черный шар достали из первой урны:
Аналогично:
По формуле полной вероятности:
Ответ: 
5) Имеются две урны: в первой 5 белых и 10 черных шаров; во второй урне 9 белых и 6 черных шаров. Из первой урны во вторую перекладывают, не глядя, один шар. После этого из второй урны достают один шар. Найти вероятность того, что этот шар будет черным.
Решение
Событие A – из второй урны достали черный шар. Событие A может произойти с одним из несовместных событий (гипотез):
H 1 – из первой урны во вторую переложили белый шар;
H 2 – из первой урны во вторую переложили черный шар.
Вероятности гипотез:
Найдем условные вероятности события A. Если из первой урны во вторую переложили белый шар, то во второй урне стало 10 белых и 6 черных шаров. Значит, вероятность достать из нее черный шар равна:
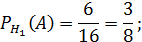
Аналогично:
По формуле полной вероятности:
Ответ: 
6) Имеются три урны: в первой 5 белых и 10 черных шаров; во второй 9 белых и 6 черных шаров; в третьей урне 15 черных шаров (белых шаров нет). Из наугад выбранной урны достали один шар. Этот шар оказался черным. Найти вероятность того, что шар достали из второй урны.
|
|
|
Решение
Событие A – из наугад выбранной урны достали один шар.
Событие A может произойти с одним из несовместных событий (гипотез):
H 1 – шар достали из первой урны;
H 2 – шар достали из второй урны;
H 3 – шар достали из третьей урны.
Априорные вероятности гипотез равны:
В задаче 4 найдены условные вероятности события A и его полная вероятность:
Найдем по формуле Байеса апостериорную вероятность гипотезы H 2.
Черный шар достали из второй урны:
Сравним 
и 
:
Таким образом, если известно, что достали черный шар, то вероятность того, что его достали из второй урны уменьшается (это соответствует условию – во второй урне меньше всего черных шаров).
Ответ: 
.
Формула Бернулли
7) В семье шесть детей. Вероятность рождения девочки равна 0,49. Найти вероятность того, что среди этих детей одна девочка.
Решение
Событие A – родилась девочка.
P = P (A) = 0,49;
q = 1 – p = 1 – 0,49 = 0,51.
Формула Бернулли:
Всего шесть детей, значит n =6.
Надо найти вероятность того, что среди них точно одна девочка, значит m = 1.
Ответ: 
8) Отрезок AB разделен точной C в отношении 2:1. На этот отрезок наудачу брошено 6 точек. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. Найти вероятность того, что более одной точки окажется правее точки C.
Решение
Событие A – случайная точка попала на отрезок CB (правее точки C).
Так как C делит AB в отношении 2:1, то:
Значит:
2 CB = AC;
2 CB + CB = AC + CB;
3 CB = AB;
Опираясь на геометрическое определение вероятности, получаем:
Формула Бернулли:
Всего на отрезок AB брошено 6 точек, значит n = 6.
Событие B – более одной точки окажется правее точки C.
Противоположное событие:
– не более одной точки окажется правее точки C, то есть ни одной точки или ровно одна точка.
Ответ: 
9) Монету бросают 6 раз. Найти вероятность того, что не более 5 раз выпадет герб.
|
|
|
Решение
Событие A – при подбрасывании монеты выпадает герб.
Монета подбрасывается 6 раз, значит n = 6.
Событие B – герб выпадет не более 5 раз.
Противоположное событие:
– герб выпадет более 5 раз, то есть 6 раз.
Ответ: 
|
|
|
