 |
Электростатическая теорема Гаусса
|
|
|
|
РИС.13-1
Не исключено, что закон сохранения заряда первичен в природе. Поэтому можно сформулировать закон сохранения заряда либо как фундаментальный постулат физики, либо как экспериментальный факт; нарушение закона сохранения заряда никогда никем не наблюдалось.
Факты
a) Нейтральность позитрония (Ps-связанная водородоподобная система электрона и позитрона, время жизни 10 –7 с).
 |
b) Нейтральность атома цезия (Cs55). Установлено, что заряд атома Cs не превышает величину 10-16 e ®55 e +55 p.
РИС.13-2
с) Нейтральность молекул водорода H2. Сжимают объем и выпускают газ, чтобы не вышли ионы водорода.
В этом опыте мог быть зафиксирован заряд около 10-20 e /атом, но он не был обнаружен. Значит, (e + p)<10-20 e.
В изолированной системе полный электрический заряд, т.е. алгебраическая сумма положительного и отрицательного зарядов, остается постоянным.
3) Полный заряд релятивистки инвариантен, т. е. алгебраическая сумма зарядов в изолированной системе не меняется при переходе от одной ИСО к другой ИСО независимо от скорости и относительного движения.
4) Квантование заряда. Опыты Милликена (1911 г.) и А.Ф. Иоффе (1912 г.).
 |
Идея опыта – в обнаружении непрерывности заряда, если они не имеют атомной природы.
РИС.13-3
Иоффе определял заряд металлических (Zn) крупинок, Милликен - масла. Мелкие капли заряженного масла попадаю в конденсатор.
Без электрического поля на каплю действут вес капли и гидростатическая сила (архимедова) со стороны воздуха и сила трения на каплю при движении в вязкой среде, пропорциональная скорости капли (закон Стокса):
 ,
,  .
.
 Þ
Þ  - отсюда, измеряя скорость падения капли, узнаем ее радиус.
- отсюда, измеряя скорость падения капли, узнаем ее радиус.
|
|
|
Включим теперь внешнее напряжение, подобрав полярность таким образом, чтобы уменьшить скорость падения капли, например, уменьшить скорость падения капли до нуля. В этом случае условие равновесия сил будет иметь вид:
 , где
, где  - заряд капли,
- заряд капли,  - напряженность приложенного электрического поля. Если капля находится достаточно далеко от краев пластин, то поле однородно и
- напряженность приложенного электрического поля. Если капля находится достаточно далеко от краев пластин, то поле однородно и  ,
,  - разность потенциалов (напряжение),
- разность потенциалов (напряжение), 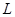 - расстояние между пластинами.
- расстояние между пластинами.
Отсюда находим заряд капли  . Если изменить заряд капли, например, воздействуя на нее ультрафиолетовым излучением, т. е. удаляя из капли заряды за счет фотоэлектрического эффекта, то нужно будет подобрать новое напряжение
. Если изменить заряд капли, например, воздействуя на нее ультрафиолетовым излучением, т. е. удаляя из капли заряды за счет фотоэлектрического эффекта, то нужно будет подобрать новое напряжение  , и отсюда выяснится новый заряд капли.
, и отсюда выяснится новый заряд капли.
Оказалось, что изменение заряда капли  всегда является целым кратным некоторой величины:
всегда является целым кратным некоторой величины: 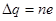 , где
, где  .
.
Современная теория элементарных частиц допускает (предполагает) существование частиц с дробным зарядом – двух типов кварков с зарядами  и
и  . Поскольку во всех проведенных до сих пор экспериментах кварки не обнаружены, высказывается предположение, что кварки не могут существовать вне частиц.
. Поскольку во всех проведенных до сих пор экспериментах кварки не обнаружены, высказывается предположение, что кварки не могут существовать вне частиц.
ЭЛЕКТРОСТАТИКА
Основные законы электростатики
Рассматривая законы электростатики, т.е. законы, определяющие поведение неподвижных зарядов, мы будем предполагать, что заряды находятся в вакууме. Практически это означает, что при исследовании зависимости свойств неподвижных зарядов от давления газа  приходится экстраполировать полученные результаты к
приходится экстраполировать полученные результаты к 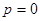 , т. е. к случаю абсолютного вакуума.
, т. е. к случаю абсолютного вакуума.
Закон Кулона (экспериментально установлен в 1785 г.). Точечные заряды (размер заряженных частиц много меньше расстояния между ними 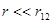 ).
).
Сила взаимодействия 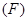 двух точечных зарядов (
двух точечных зарядов ( и
и 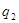 ) в вакууме направлена по прямой, соединяющей эти заряды, пропорциональна их величинам
) в вакууме направлена по прямой, соединяющей эти заряды, пропорциональна их величинам  и
и 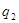 и обратно пропорциональна квадрату расстояния между ними.
и обратно пропорциональна квадрату расстояния между ними.
Из принципа дуализма электрического заряда следует, что сила взаимодействия будет силой притяжения, если взаимодействующие заряды разноименные, и силой отталкивания, если взаимодействующие заряды одноименные.
|
|
|
Математически:  .
.
В абсолютной электростатической системе единиц (CGSE) единица заряда выбирается так, чтобы  .
.
 ,
, 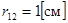 ,
, 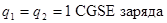 , т. е. получается так, что в системе CGSE заряд – это производная единица, определяемая из закона Кулона.
, т. е. получается так, что в системе CGSE заряд – это производная единица, определяемая из закона Кулона.
Размерность заряда:  [дина] = [г×см×с-2] =
[дина] = [г×см×с-2] =  ;
;  .
.
За единицу заряда в системе CGSE (или в абсолютной электростатической системе единиц) принимается величина такого точечного заряда, который действует на такой же точечный заряд в вакууме с силой в 1 дину, если расстояние между зарядами равно 1 см.
В системе SI размерность и величина заряда задаются независимо: в качестве единицы заряда принимается 1Кл=1А×1с. Задаются также единица расстояния  и единица силы
и единица силы  . Поэтому коэффициент
. Поэтому коэффициент  в законе Кулона с неизбежностью будет размерным и, вероятно, не равен 1.
в законе Кулона с неизбежностью будет размерным и, вероятно, не равен 1.
Из технических соображений записывают
 , где
, где  - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума.
Напряженность электрического поля
Сила, действующая на единичный неподвижный электрический заряд, называется напряженностью электрического поля  .
.
Если, например,  , то
, то  , где
, где  - расстояние от данного заряда до
- расстояние от данного заряда до 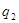 (пробного заряда).
(пробного заряда).
Сила, действующая на неподвижный заряд:  .
.
В векторной форме.
Закон Кулона:  ,
,
где 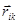 - радиус-вектор, проведенный от заряда
- радиус-вектор, проведенный от заряда  к заряду
к заряду  .
.
Напряженность электрического поля, создаваемого точечным зарядом  :
:
 , где
, где 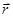 - радиус-вектор, проведенный от заряда
- радиус-вектор, проведенный от заряда  в точку, к которой относится наблюдаемое электрическое поле.
в точку, к которой относится наблюдаемое электрическое поле.
 |
Принцип суперпозиции: Сила взаимодействия двух зарядов не изменяется при наличии третьего заряда:
РИС.13-4
 .
.
Для напряженности электрического поля:
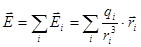 , где
, где  - радиус-вектор, проведенный из точки, где находится заряд
- радиус-вектор, проведенный из точки, где находится заряд  , в точку наблюдения.
, в точку наблюдения.
Если заряд не является точечным, то его следует мысленно разделить на части, каждую из которых можно считать точечным зарядом, а затем просуммировать результаты. Если разделение заряда непрерывное, то суммирование заменяется интегрированием.
Возможно, что принцип суперпозиции нарушается на очень малых расстояниях, порядка размеров ядер, 10-12-10-13 см, где нет уверенности в справедливости электромагнитной теории вообще.
|
|
|
Экспериментальная проверка справедливости закона Кулона была выполнена в пределах 100-10-1 см, где он выполняется с точностью до 10-7-7-7%.
Для расстояний географических, или тем более астрономических, справедливость закона Кулона экспериментально не проверялась. Однако, если бы он был несправедлив, то наблюдалась бы зависимость скорости распространения электромагнитных волн в вакууме от длины волны (так как оказалось бы, что фотон имеет ненулевую массу покоя). Зависимость  от
от 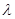 не обнаружена (на Земле были одновременно зафиксированы световой сигнал и радиоизлучение сверхновой звезды, находящейся от нас на расстоянии 20 световых лет).
не обнаружена (на Земле были одновременно зафиксированы световой сигнал и радиоизлучение сверхновой звезды, находящейся от нас на расстоянии 20 световых лет).
Электростатическая теорема Гаусса
Поток вектора – одно из важнейших понятий векторного анализа, оно используется при описании свойств электрического, магнитного, гидродинамического полей.
 |
Простейший пример: поток жидкости со скоростью
 .
.
РИС.13-5
Объем жидкости, вытекающей через малую площадку  за время
за время  :
: 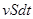 .
.
Площадку  нужно выбрать такой малой, чтобы можно было полагать, что в ее пределах величина и направление вектора
нужно выбрать такой малой, чтобы можно было полагать, что в ее пределах величина и направление вектора  не меняются.
не меняются.
Если площадка наклонна, то 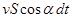 , где
, где  ,
,  - внешняя нормаль площадки.
- внешняя нормаль площадки.
В любом случае в единицу времени через площадку будет протекать. 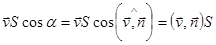 .
.
Для элементарной площадки 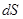 :
:  .
.
Определение.
Назовем потоком  вектора
вектора  через элемент поверхности
через элемент поверхности 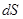 , характеризуемый направлением нормали
, характеризуемый направлением нормали  , величину
, величину  .
.
Через некоторую конечную поверхность  поток получим путем сложения потоков через элементарные поверхности
поток получим путем сложения потоков через элементарные поверхности 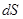 :
:  .
.
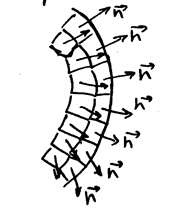 |
РИС.13-6
Полученный результат справедлив для любого поля и любой поверхности, лишь бы поверхность была достаточно гладкая и не проходила бы через точки, где поле имеет особенность (точечный заряд, какой-нибудь иной разрыв величины и напряженности поля).
 |
Рассмотрим интересующий нас случай, когда в точке O находится точечный заряд
 , и вычислим поток вектора
, и вычислим поток вектора  через бесконечно малую площадку
через бесконечно малую площадку 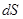 .
.|
|
|
РИС.13-7
 ;
; 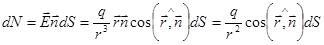 .
.
Произведение  численно равно площади проекции
численно равно площади проекции 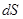 на плоскость, перпендикулярную
на плоскость, перпендикулярную 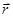 , т.е. площадке
, т.е. площадке 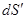 .
.
Если из точки O «видна» внутренняя сторона площадки 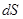 , т.е.
, т.е.  - внешняя нормаль, то
- внешняя нормаль, то  (угол острый); напротив, если мы перенесем точку О таким образом, что станет видна «наружная» сторона площадки, то угол будет тупым,
(угол острый); напротив, если мы перенесем точку О таким образом, что станет видна «наружная» сторона площадки, то угол будет тупым,  .
.
Следует заметить, что понятие о положительном направлении единичного вектора нормали к площадке – сугубо условное. Принято считать положительным «внешнее» направление: вектор  исходит из внешней поверхности (входит во внутреннюю).
исходит из внешней поверхности (входит во внутреннюю).
Итак:  .
.
Телесный угол, под которым площадка 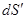 видна из точки О, есть
видна из точки О, есть
 .
.
Поток вектора  через площадку
через площадку 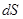 :
:
 .
.
С другой стороны:  - проекция вектора
- проекция вектора  на направление нормали к площадке.
на направление нормали к площадке.
Следовательно:  .
.
Получили: поток  вектора электрического поля точечного заряда
вектора электрического поля точечного заряда  через произвольно ориентированную площадку
через произвольно ориентированную площадку 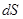 зависит только от телесного угла, под которым видна площадка
зависит только от телесного угла, под которым видна площадка 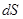 из точки, в которой находится заряд
из точки, в которой находится заряд  .
.
Полный поток через конечную поверхность  :
:
 , где
, где 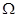 - положительный или отрицательный телесный угол, под которым видна из точки
- положительный или отрицательный телесный угол, под которым видна из точки  вся поверхность
вся поверхность  .
.
Если поверхность  - замкнутая, то
- замкнутая, то 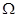 может иметь только два значения,
может иметь только два значения,  или 0 в зависимости от того, находится заряд внутри поверхности или вне ее.
или 0 в зависимости от того, находится заряд внутри поверхности или вне ее.
Случай, когда заряд находится на поверхности, мы не рассматриваем, так как в этом случае электрическое поле на поверхности обращается в бесконечность, и эта поверхность уже не удовлетворяет поставленному условию – чтобы на ней не было разрывов или особенностей исследуемого поля.
 |
I. Заряд внутри поверхности: она окружает его со всех сторон и видна, следовательно, под полным телесным углом
 :
:  . Так всегда, когда прямая, исходящая из заряда, пересекает окружающую поверхность нечетное число раз.
. Так всегда, когда прямая, исходящая из заряда, пересекает окружающую поверхность нечетное число раз.
РИС.13-8
Угол  , под которым видны площадки
, под которым видны площадки  , одинаков по абсолютной величине, но
, одинаков по абсолютной величине, но  , так как площадки
, так как площадки  обращены к
обращены к  внутренними сторонами.
внутренними сторонами.
II. Если заряд расположен вне поверхности, то прямая, проведенная из заряда, пересекает поверхность четное число раз (0 – тоже четное число!). Части поверхности  и
и  видны из точки О под углами
видны из точки О под углами  и
и  , которые равны по величине и противоположны по знаку, так что
, которые равны по величине и противоположны по знаку, так что  .
.
 |
РИС.13-9
Если под  понимать заряд, охватываемый поверхностью
понимать заряд, охватываемый поверхностью  , то оба случая объединяются в один:
, то оба случая объединяются в один:  .
.
Для любой системы зарядов в соответствии с принципом суперпозиции:
 ,
,  ,
,
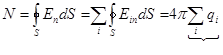 (суммирование по всем зарядам внутри поверхности
(суммирование по всем зарядам внутри поверхности  ).
).
Если внутри поверхности имеется распределенный (объемный) заряд  , то сумма заменится интегралом по объему:
, то сумма заменится интегралом по объему:  .
.
|
|
|
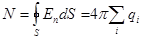 ;
; 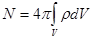 .
.
Полученные результаты выражают фундаментальную теорему Гаусса (электростатическую).
Поток вектора напряженности электрического поля  в вакууме через произвольную замкнутую поверхность равен умноженной на
в вакууме через произвольную замкнутую поверхность равен умноженной на  величине заряда, охватываемого этой поверхностью.
величине заряда, охватываемого этой поверхностью.
Теорема Гаусса справедлива для любых векторных полей, напряженность которых  , например, для гравитационного поля.
, например, для гравитационного поля.
Теорема Гаусса несправедлива для векторных полей, напряженность которых зависит от расстояния иначе, чем  , например,
, например,  . В этом последнем случае поток будет зависеть от расстояния как
. В этом последнем случае поток будет зависеть от расстояния как  , т. е. при
, т. е. при  , хотя свойства зарядов не меняются; этот результат противоречит здравому смыслу.
, хотя свойства зарядов не меняются; этот результат противоречит здравому смыслу.
Примеры применения теоремы Гаусса
Для расчета электрических полей сложной системы зарядов теоремы Гаусса недостаточно, так как одного скалярного уравнения недостаточно для определения трех компонент вектора  .
.
Электростатическое поле бесконечной равномерно заряженной плоскости
 |
РИС.13-10
Поверхностный заряд  . Вектор
. Вектор  плоскости (по соображениям симметрии).
плоскости (по соображениям симметрии).
 - площадь каждого из оснований. Поток вектора
- площадь каждого из оснований. Поток вектора  через каждое из оснований
через каждое из оснований  , а через оба основания
, а через оба основания 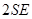 . Поток через боковую поверхность равен нулю, так как
. Поток через боковую поверхность равен нулю, так как  . Значит, поток через весь цилиндр
. Значит, поток через весь цилиндр 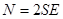 .
.
С другой стороны, по теореме Гаусса имеем  .
.
Приравнивая оба выражения, находим:  Þ
Þ
 .
.
Поле бесконечно заряженной плоскости не зависит от расстояния до плоскости постольку, поскольку это расстояние мало по сравнению с размерами плоскости. Так как по разные стороны плоскости вектора  одинаковы по величине, но противоположны по направлению, поэтому при переходе через заряженную плоскость напряженность электрического поля (точнее – ее нормальная компонента) меняется скачком на
одинаковы по величине, но противоположны по направлению, поэтому при переходе через заряженную плоскость напряженность электрического поля (точнее – ее нормальная компонента) меняется скачком на  :
:
 .
.
Поле шара, равномерно заряженного по поверхности или по объему
 |
Сферическая симметрия задачи приводит к тому, что вектор
 параллелен или антипараллелен радиусу - вектору
параллелен или антипараллелен радиусу - вектору 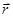 , проведенному из центра шара в точку наблюдения.
, проведенному из центра шара в точку наблюдения.
РИС.13-11
Поток вектора  через сферу
через сферу  по теореме Гаусса
по теореме Гаусса  и
и 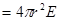 . Приравнивая, находим:
. Приравнивая, находим:  , т.е. как будто весь заряд находится в центре шара.
, т.е. как будто весь заряд находится в центре шара.
Если радиус  , то
, то 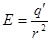 , где
, где  - заряд, ограниченный сферой радиуса
- заряд, ограниченный сферой радиуса  .
.
Если заряд равномерно распределен по сфере с объемной плотностью  (
( ), то
), то  и напряженность поля
и напряженность поля  .
.
Если заряд равномерно распределен по поверхности сферы, то  и
и  .
.
Электрическое поле внутри сферической полости, равномерно заряженной по поверхности, равно нулю.
14 Дифференциальная форма теоремы Гаусса
Математическое отступление
Поток некоторого вектора через замкнутую поверхность  :
:
 .
.
Этот поверхностный интеграл можно преобразовать в объемный с использованием
 |
теоремы Гаусса из векторного анализа.
РИС.14-1
 - произвольный дифференцируемый вектор. Рассмотрим поток вектора через поверхность бесконечно малого параллелепипеда
- произвольный дифференцируемый вектор. Рассмотрим поток вектора через поверхность бесконечно малого параллелепипеда  .
.
 , где
, где 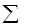 - по граням параллелепипеда, а интеграл берется по каждой грани; поскольку грани бесконечно малы, можно брать среднее значение по грани.
- по граням параллелепипеда, а интеграл берется по каждой грани; поскольку грани бесконечно малы, можно брать среднее значение по грани.
Рассматриваем поток через грани (1) и (2),  .
.
Через грань (2):
 .
.
Через грань (1):
 (возникает знак минус, так как вектор внешней нормали направлен в отрицательную сторону оси
(возникает знак минус, так как вектор внешней нормали направлен в отрицательную сторону оси  ).
).
Суммарный поток через грани (1) и (2):
 , где в скобках изменение
, где в скобках изменение  компоненты вектора
компоненты вектора  при изменении координаты от
при изменении координаты от  до
до  .Из дифференциального исчисления известно, что приращение величины функции нескольких переменных при изменении одного из аргументов на бесконечно малую величину равно (с точностью до величин второго порядка малости):
.Из дифференциального исчисления известно, что приращение величины функции нескольких переменных при изменении одного из аргументов на бесконечно малую величину равно (с точностью до величин второго порядка малости):
 ,
,  .
.
{По определению производной  }
}
Поток через грани (1) и (2) будет:
 .
.
Полный поток вектора  по всем шести граням:
по всем шести граням:
 .
.
Итак, поток произвольно дифференцируемого вектора  через бесконечно малый параллелепипед:
через бесконечно малый параллелепипед:  .
.
Определение дивергенции произвольного дифференциального вектора:
 .
.
Дивергенцией вектора  в данной точке называется предел, к которому стремится отношение потока вектора через малую (произвольную) поверхность
в данной точке называется предел, к которому стремится отношение потока вектора через малую (произвольную) поверхность 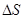 , окружающую эту точку, к величине ограниченного этой поверхностью объема
, окружающую эту точку, к величине ограниченного этой поверхностью объема  при
при  .
.
Из определения следует, что величина дивергенции не зависит от выбора системы координат и, следовательно, дивергенция вектора – скаляр.
Можно записать  с использованием векторного оператора набла
с использованием векторного оператора набла  (стрелка обычно не ставится):
(стрелка обычно не ставится):
 ;
;  .
.
Составим скалярное произведение:
 .
.
Представление о дивергенции становится более наглядным, если рассматривать дивергенцию вектора скорости жидкости  :
:
 (в числителе - количество жидкости, вытекающей из объема
(в числителе - количество жидкости, вытекающей из объема  , окружающего рассматриваемую точку.
, окружающего рассматриваемую точку.
Значит, жидкость будет вытекать из тех точек, где  ; очевидно, что в этих точках должны находиться источники жидкости.
; очевидно, что в этих точках должны находиться источники жидкости.
Определения
Те точки поля произвольного вектора  , в которых
, в которых  , называют истоками тока, а
, называют истоками тока, а 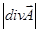 называют силой или обильностью истоков.
называют силой или обильностью истоков.
Если  в некоторых точках, говорят, что в этих точках находятся стоки поля.
в некоторых точках, говорят, что в этих точках находятся стоки поля.
Векторные поля, у которых 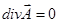 , называют свободными от источников, или соленоидальными.
, называют свободными от источников, или соленоидальными.
Итак, в пределе поток через бесконечно малую поверхность, окружающую данную точку:  .
.
|
|
|


