 |
Сила, действующая на диполь
|
|
|
|
 .
.
Если электрическое поле однородно,  и равнодействующая
и равнодействующая  .
.
Однако на диполь действует момент сил  .
.
Отсюда вывод: диполь стремится повернуться в электрическом поле так, чтобы его момент был параллелен (антипараллелен, но это положение не устойчиво) полю E.
Если электрическое поле неоднородно, то  .
.
Для точечного диполя  (приращение поля на отрезке
(приращение поля на отрезке  , равном плечу диполя):
, равном плечу диполя):
 .
.
Сила: 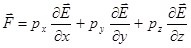 .
.
Скалярное произведение:  .
.
В этих обозначениях  .
.
Эта сила направлена в сторону возрастания электрического поля: диполь втягивается в область сильного поля.
Другая формулировка для пондеромоторных сил, из выражения для энергии
 ,
,
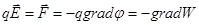 .
.
 .
.
Сила, действующая на пластины плоского конденсатора.
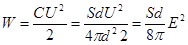 ,
,
 .
.
Или:  ,
,
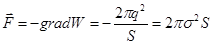 .
.
Сила, создаваемая поверхностным зарядом:  - в полном согласии с полученным ранее результатом:
- в полном согласии с полученным ранее результатом: 
Вопрос об устойчивости электрических систем. Теорема Ирншоу
(дополнительный материал)
Для электрической теории строения материи весьма важен вопрос о возможности существования устойчивых конфигураций электрических зарядов (электронов и протонов). Может ли эта система находиться в статическом равновесии или же в атомах и молекулах эти частицы должны находиться в непрерывном движении?
Как это выяснить?
Электрическая энергия играет роль потенциальной энергии – в этом мы уже убедились. Условие устойчивости любой системы – нахождение ее в состоянии минимума потенциальной энергии - ищем  .
.
 ,
,  .
.
Условия min:
1)  ; {
; {  - координата любого заряда}
- координата любого заряда}
2)  , или
, или 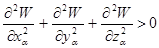 , так как min не достигается, если хотя бы одна из вторых производных
, так как min не достигается, если хотя бы одна из вторых производных  .
.
 .
.
 =0, если
=0, если  .
.
Если  или
или  , то
, то  = 0 в силу того, что вообще
= 0 в силу того, что вообще  = 0 в любой точке P.
= 0 в любой точке P.
Это можно показать:  = 0 (если
= 0 (если  ).
).
|
|
|
Принимаем точку P за начало координат.
Тогда  ,
,
 .
.
 ;
;
 .
.
Отсюда:
 - что и требовалось доказать.
- что и требовалось доказать.
Из изложенного следует, что  - потенциальная энергия не имеет минимума, следовательно (теорема Ирншоу):
- потенциальная энергия не имеет минимума, следовательно (теорема Ирншоу):
статическая система электрических зарядов не является устойчивой.
Физический смысл: разноименные заряды притягиваются вплоть до взаимного уничтожения, а одноименные отталкиваются вплоть до удаления в бесконечность.
Общая мораль:
1) атом должен представлять собой динамическую систему;
2) поскольку теорема Ирншоу исходит только из одного обстоятельства – сила взаимодействия 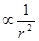 , значит, устойчивость нашей планетной системы обусловливается лишь движением планет.
, значит, устойчивость нашей планетной системы обусловливается лишь движением планет.
Статическая система, которую мы здесь рассматривали, может быть устойчивой лишь при наличии дополнительных сил неэлектрического происхождения.
16 Основные итоги, касающиеся электростатики в вакууме
| Интегральная форма | Дифференциальная форма | |

| 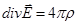

| (1) |

| 

| (2) |

| 

| (3) |
Из (1) и (3) мы легко получили уравнение Пуассона:
 , где
, где  , которое в отсутствие объемных зарядов переходит в уравнение Лапласа
, которое в отсутствие объемных зарядов переходит в уравнение Лапласа  . Уравнение Пуассона было решено для некоторых частных случаев.
. Уравнение Пуассона было решено для некоторых частных случаев.
Затем было введено представление о потенциальной энергии взаимодействия точечных зарядов, которую мы представляем в симметричной форме:
 ,
,  - потенциал всех зарядов в точке нахождения
- потенциал всех зарядов в точке нахождения  -го заряда.
-го заряда.
Полученные результаты можно обобщить на случай объемных и поверхностных зарядов.
Если разбить эти заряды на элементарные  и
и 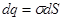 , то
, то
 , где
, где 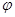 - значение потенциала всех объемных и всех поверхностных зарядов в элементе объема
- значение потенциала всех объемных и всех поверхностных зарядов в элементе объема  или на элементе поверхности
или на элементе поверхности 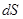 .
.
Воспользовавшись теоремой Грина

или

(где  - любые непрерывные конечные скалярные функции координат, обладающие в области интегрирования производными первого и второго порядков), мы нашли
- любые непрерывные конечные скалярные функции координат, обладающие в области интегрирования производными первого и второго порядков), мы нашли
 и ввели представление об объемной плотности энергии
и ввели представление об объемной плотности энергии  .
.
|
|
|
Поиски минимума потенциальной энергии взаимодействия  точечных зарядов привели нас к заключению, что электростатическое взаимодействие не обеспечивает устойчивого состояния статической системы электрических зарядов (теорема Ирншоу).
точечных зарядов привели нас к заключению, что электростатическое взаимодействие не обеспечивает устойчивого состояния статической системы электрических зарядов (теорема Ирншоу).
Физический смысл: разноименные заряды притягиваются вплоть до взаимного уничтожения, а одноименные отталкиваются вплоть до удаления в бесконечность.
Следовательно:
1) атом должен представлять собой динамическую систему, в которой действуют силы неэлектрического происхождения;
2) любая система, где действуют только силы 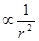 , не будет статически устойчивой; устойчивость нашей планетной системы обусловливается лишь движением планет.
, не будет статически устойчивой; устойчивость нашей планетной системы обусловливается лишь движением планет.
ДИЭЛЕКТРИКИ
Введение
Диэлектрики – в отличие от металлов и полупроводников – не имеют свободных носителей заряда, свободных – чтобы перемещаться под действием электрического поля.
Два главных типа диэлектриков.
1) Молекулярные диэлектрики. Вещество состоит из нейтральных молекул – это жидкие, аморфные и газообразные вещества, молекулярные кристаллы, в том числе жидкие кристаллы. Вещество в целом нейтрально. В зависимости от типа молекул молекулярные диэлектрики подразделяются на два класса:
а) неполярные, электрический момент каждой молекулы равен нулю,  ;
;
б) полярные, электрический момент каждой молекулы не равен нулю,  , но в достаточно большом объеме
, но в достаточно большом объеме  .
.
2) Ионные диэлектрики (например, NaCl). Вещество нейтрально в целом, нейтральна каждая элементарная ячейка. Положительные и отрицательные заряды достаточно жестко закреплены в положениях равновесия.
Заряды - в диэлектриках обоих типов – не могут под действием внешнего электрического поля перемещаться таким образом, чтобы приобрести конечную скорость направленного движения (дрейф), они могут лишь немного сместиться из положения равновесия (в ионных кристаллах и в молекулярных неполярных), при этом в каждой молекуле возникает  такой, что
такой, что  , или могут повернуться так (в полярных диэлектриках), чтобы
, или могут повернуться так (в полярных диэлектриках), чтобы  (а без поля был равен нулю).
(а без поля был равен нулю).
Поэтому с формальной точки зрения можно обе разновидности диэлектриков (в целом нейтральных диэлектриков,  ) описывать вектором электрической поляризации системы
) описывать вектором электрической поляризации системы 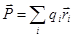 , где суммирование производится по всем электронам и ядрам системы и
, где суммирование производится по всем электронам и ядрам системы и  - это радиус-вектор, проведенный к заряду
- это радиус-вектор, проведенный к заряду  из произвольной точки О. Покажем, что смещение начала отсчета не меняет
из произвольной точки О. Покажем, что смещение начала отсчета не меняет 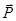 .
.
|
|
|
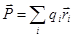 ,
,
 |
РИС.16-1
 .
.
 |
Вычислим вектор электрической поляризации системы, состоящей из двух точечных зарядов
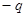 и
и 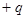 .
.
РИС.16-2
 , как было получено ранее.
, как было получено ранее.
В поляризованном диэлектрике возникают объемные заряды (хотя в целом диэлектрик нейтрален), т.е.  .
.
Поэтому потенциал, создаваемый поляризованным диэлектриком в некоторой точке 1, есть 
 , где
, где 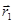 - расстояние от данной точки объема диэлектрика до точки наблюдения.
- расстояние от данной точки объема диэлектрика до точки наблюдения.

РИС.16-3
Вычисляя потенциал на достаточно большом расстоянии от диэлектрика,  , убеждаемся, что это потенциал вида
, убеждаемся, что это потенциал вида  - т.е. дипольный потенциал (главный по величине) + поправки ~
- т.е. дипольный потенциал (главный по величине) + поправки ~  - квадрупольный потенциал и т.д.
- квадрупольный потенциал и т.д.
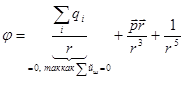 [квадрупольные члены, существенные лишь на малых расстояниях].
[квадрупольные члены, существенные лишь на малых расстояниях].
Следовательно, в первом приближении поле, возбуждаемое в целом нейтральной системой зарядов, совпадает с полем эквивалентного диполя.
Можно также показать, что потенциальная энергия совпадает по виду с выражением для энергии диполя: 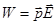 .
.
Электрическим моментом можно охарактеризовать состояние не только отдельной молекулы, но и состояние макроскопического объема диэлектрика:
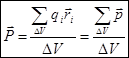 - электрический момент единицы объема.
- электрический момент единицы объема.
Поляризация диэлектрика – это векторная сумма электрических моментов молекул, находящихся в единице объема.
Потенциал электрического поля при наличии диэлектриков
Свободные заряды:
1) электроны и ионы, которые могут перемещаться;
2) все заряды, нарушающие нейтральность диэлектрика в целом, например, внесенные на его поверхность.
Связанные заряды:
заряды, входяшие в состав нейтральных молекул диэлектрика, например, ионы, закрепленные вблизи положения равновесия.
Принцип суперпозиции полей позволяет утверждать, что потенциал 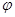 электростатического поля в диэлектрике складывается из потенциала
электростатического поля в диэлектрике складывается из потенциала  свободных зарядов и потенциала
свободных зарядов и потенциала 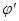 связанных зарядов:
связанных зарядов:
|
|
|
 .
.
Потенциал свободных зарядов  :
:
 (
( - объемная и поверхностная плотности зарядов).
- объемная и поверхностная плотности зарядов).
Потенциал связанных зарядов 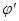 :
:
электрический момент элемента объема  ,
,
потенциал, создаваемый этим элементом объема  (обычный дипольный потенциал),
(обычный дипольный потенциал),
потенциал всего поляризованного объема
 .
.
Итак, 
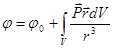 .
.
Преобразуем подынтегральное выражение:
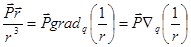 {
{  - градиент численной величины радиуса - вектора, рассматриваемого как функция точки истока}
- градиент численной величины радиуса - вектора, рассматриваемого как функция точки истока}
Градиент численной величины радиус-вектора r, как функция т. истока, задается следующим образом:
 .
.
При этом 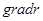 - задает только направление, его абсолютная величина =1
- задает только направление, его абсолютная величина =1
Из векторного анализа:
 ,
,
 ,
,
 ,
,  ;
;
 {
{ 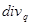 - можно не подчеркивать, что
- можно не подчеркивать, что 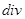 относится к истоку, так как она отлична от нуля лишь на истоках}.
относится к истоку, так как она отлична от нуля лишь на истоках}.
Получаем:  .
.
По теореме Гаусса
 {
{  выделяет области, где вектор
выделяет области, где вектор 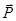 терпит разрыв}.
терпит разрыв}.
При стягивании  , т.е. при переходе от интегрирования по поверхности просто к двукратному интегрированию по поверхности разрыва – сначала по одной стороне (
, т.е. при переходе от интегрирования по поверхности просто к двукратному интегрированию по поверхности разрыва – сначала по одной стороне ( ), затем по другой стороне (
), затем по другой стороне ( ), имеем:
), имеем:
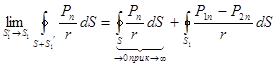 .
.
Получили:
 .
.
Формально обозначим:
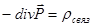 ,
,
 .
.
Получаем:  .
.
Получили:
чтобы определить поле (потенциал и напряженность электрического поля) при наличии диэлектриков нужно к свободным зарядам добавить связанные, а внешний вид формул остается тем же самым.
Следовательно,  .
.
Но мы обозначили:  .
.
Отсюда:  ,
,
 .
.
Введем вместо  новый вектор электрической индукции
новый вектор электрической индукции
 .
.
Единственное общее для  и
и 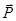 - это их размерность
- это их размерность  .
.
Отсюда:
 - уравнение Максвелла №4.
- уравнение Максвелла №4.
В вакууме  , и это уравнение переходит в свой частный случай:
, и это уравнение переходит в свой частный случай: 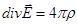 .
.
Обобщение электростатической теоремы Гаусса:
 .
.
В большинстве случаев поляризуемость прямо пропорциональна (связана линейно) электрическому полю:
 , где
, где  - тензор поляризуемости (электрической восприимчивости).
- тензор поляризуемости (электрической восприимчивости).
В изотропных диэлектриках:  .
.
Тогда:  ,
,
 - диэлектрическая проницаемость.
- диэлектрическая проницаемость.
 Þ
Þ  .
.
{Вообще  ,
,  - тензор диэлектрической проницаемости}.
- тензор диэлектрической проницаемости}.

Поверхностные заряды в вакууме
РИС.16-4
Нами было обозначено:  .
.
 ,
,
 ,
,
 , где
, где 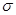 - плотность свободных зарядов.
- плотность свободных зарядов.
 - на границе с металлом (направление
- на границе с металлом (направление  - от металла к диэлектрику).
- от металла к диэлектрику).
При отсутствии свободных зарядов:  ,
,  .
.
Граница раздела двух сред
Если имеем границу раздела двух сред (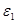 и
и  ):
):  .
.
Если на границе нет свободных зарядов, т.е.  ,
, 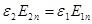 ;
;  .
.
Рассуждения о границе раздела двух диэлектриков не меняют вывода о тангенциальной составляющей напряженности электрического поля:
 , или
, или  Þ
Þ  .
.
На границе раздела двух сред нормальная компонента  непрерывна, тангенциальная компонента
непрерывна, тангенциальная компонента  непрерывна.
непрерывна.
Уравнения поля в произвольной среде.
|
|
|

 ;
;
 ;
;
 ;
;
 .
.
 ,
,  ,
,

 ,
,
 ,
,  ;
;
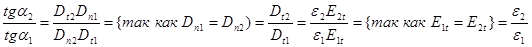 .
.
 - закон преломления линий индукции.
- закон преломления линий индукции.
Электрическое поле в однородном диэлектрике
Если диэлектрик однороден, то и поляризуемость (электрическая восприимчивость) и диэлектрическая проницаемость не зависят от координат.
 .
.
Отсюда  (
( - плотность свободных зарядов).
- плотность свободных зарядов).
Отсюда следует:  ;
; 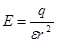 (обобщенный закон Кулона – справедлив только в однородном диэлектрике).
(обобщенный закон Кулона – справедлив только в однородном диэлектрике).
Отсюда: если между обкладками конденсатора помещается однородный диэлектрик, то потенциал уменьшается в  раз, следовательно (
раз, следовательно ( ) емкость конденсатора возрастает в
) емкость конденсатора возрастает в  раз.
раз.
Для плоского конденсатора:  . Наконец, в однородной среде:
. Наконец, в однородной среде:  .
.
|
|
|


