 |
Знаки и индексы, нанесенные на линейке
|
|
|
|
Назначение и устройство НЛ – 10м. Назначение шкал.
Навигационная счетная линейка НЛ-10 предназначена для выполнения необходимых расчетов в полете и на земле при подготовке к полету. Она обладает рядом достоинств. При сравнительно небольших габаритах счетная линейка позволяет довольно просто и с достаточной для практических вычислений точностью решать большинство задач по самолетовождению, бомбометанию, воздушной стрельбе и т. д.
Конструкция счетной линейки
Линейка НЛ-10 (рис. 2) имеет три основные части: корпус 1, движок 2 и визирку 3,
Корпус линейки состоит из двух брусков, изготовленных из выдержанного дерева, стойкого к изменению температуры и влажности. С обоих концов бруски соединены двумя металлическими скрепами 4. Один из брусков имеет косой срез.
Движок, изготовленный из того же дерева, с некоторым трением может передвигаться между брусками корпуса Он удерживается от выпадения специальными стопорами.
Шкалы специальной краской нанесены способом глубокого тиснения на белом целлулоиде (или на целлулоиде, содержащем люминесцирующий состав) и наклеены на корпус и движок линейки.
Визирка с двух сторон охватывает корпус линейки и может передвигаться вдоль него, постоянно прижимаясь к одному из брусков корпуса при помощи небольшой пружины. Рабочая часть визирки изготовлена из прозрачного целлулоида, и на обеих сторонах ее перпендикулярно шкалам нанесены риски.
Линейка имеет следующие размеры:
— длина — 29,8 см;
— ширина (по нижней части) — 4,3 см;
— толщина (без визирки) — 0,9 см.
Шкалы линейки, их назначение и построение
На счетной линейке НЛ-10 нанесено 16 вычислительных шкал, служащих для решения различных задач, и одна масштабная миллиметровая шкала. Расположение, нумерация и данные шкал показаны в таблице и на рис. 3.
|
|
|
Данные шкал НЛ-10
| № п/п | Наименование (назначение) шкал | Интервалы шкалы | Цена делений по интервалу шкалы | |
| наименьшая | наибольшая | |||
| 1. | Расстояние (км) – скорость (км/ч) | 1-1000 км(км/ч) | 0,1 км(км/ч) | 20 км (км/ч) |
| 2. | Время (в мин. или сек.) | 1 сек. – 16,6 мин | 1/6 сек. | 0,5 мин. |
| 3. | Синусы | 5 - 90° (90 – 175°) | 1° | 10° |
| 4. | Тангенсы | 0,5 - 85° | 10' | 1° |
| 5. | Радиусы разворота – расстояние - высоты | 1 – 1000м (км) | 0,1 м (км) | 20 м (км) |
| 6. | Шкала квадратных корней | 1 – 31,6 | 0,1 | 0,5 |
| 7. | Сумма температур t0+tH | от +90 до -120° | 10° | 10° |
| 8. | Исправленная высота | 400 – 12 000 м | 50м | 200м |
| 9. | Высота по прибору | 400 – 12 000 м | 50м | 200м |
| 10. | Температура на высоте для высоты более 11000м | от -30° до -75° | 5° | 5° |
| 11. | Температура на высоте для скорости | от +30° до -75° | 10° | 10° |
| 12. | Высота по прибору (км) | 0 – 12 км | 0,5 км | 0,5 км |
| 13. | Высота по прибору (км) для КУС | 0 – 11 км | 1 км | 1 км |
| 14. | Исправленная высота и скорость | 12 – 25 км 100 – 1400 км/ч | 20 м 2 км/час | 200 м 20 км/час |
| 15. | Высота и скорость по прибору | 12 – 23 км 100 – 1200 км/час | 20м 2 км/час | 200м 20 км/час |
| 16. | Шкала поправок к термометру Δt° | 0 - 51° | 1° | 5° |
| 17. | Масштабная миллиметровая шкала | 0 – 25см | 1мм | 1мм |
Знаки и индексы, нанесенные на линейке
π = 3,14 —отношение длины окружности к диаметру; нанесен на шкале 1 и может использоваться для решения задач, связанных с определением длины окружности;
t 360 —нанесен на шкале 1, служит для определения времени разворота самолета на 360°;
— нанесен краcной краской на шкале 2, служит для перевода скоростей, выраженных в км/час, в м/сек и обратно, соответствует делению 36;
—нанесен красной краской на шкале 2, служит для решения задач, связанных с определением времени полета, пройденного расстояния и путевой скорости, соответствует делению 60 минут или 1 час (60 секунд или 1 минута);
|
|
|
—нанесены на шкале 2 и могут использоваться как начальные или конечные штрихи шкалы;
® —нанесен красной краской на шкале 4 и служит для решения задач по определению радиуса разворота самолета;
—нанесен на шкале 4, соответствует делению 45° и используется для решения задач, в которые входят тригонометрические функции углов;
— нанесен на движке под шкалой 7 и служит для решения задач по определению показаний барометрических высотомеров в полете до высоты 12 000 м.
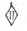— нанесен на шкале 12 и служит для решения задач по определению показаний барометрических высотомеров в полете для высот более 12 000 м.
— нанесены на шкалах 14 и 15 и служат для обозначения десятичных интервалов шкал, используются для умножения и деления чисел;
— деление шкалы 4, используется при решении задач по определению времени разворота самолета на 360°.
Для решения задач несколько шкал линейки НЛ-10м, как правило, используются одновременно. Шкалы, при помощи которых производят решение задач по определенным формулам, называются смежными. Обычно они построены по одному закону и в одном масштабе.
Рассмотрим последовательно назначение и построение всех смежных шкал линейки НЛ-10м.
Шкалы 1 — расстояние (км) — скорость км/час, 2 — время (в мин. или сек.) —время (в час. или мин.) в основном служат для решения формулы
S = Wt, (1)
где S — расстояние в км (м);
W — путевая скорость в км/час (м/сек);
t — время полета в час., мин. или сек.
На корпусе линейки на неподвижной шкале 1 в определенном масштабе нанесены деления, соответствующие значению логарифмов чисел от 1 до 1000, имеющих размерность расстояния в м или км и скорости в км/час или м/сек. Эти значения в 10,100 и т. д. раз можно увеличивать или уменьшать.
На нижней подвижной шкале 2 (на движке линейки) в том же масштабе нанесены деления, соответствующие значению логарифмов чисел от 1 до 1000, но оцифрованные в единицах времени от 1 минуты до 16,6 часа или от 1 секунды до 16,6 минуты.
В середине шкалы имеется выделенный индексами 
десятичный интервал, которым пользуются одновременно со шкалой 1 при умножении и делении безразмерных величин.
На рис. 4 показана схема решения задач по этим шкалам. Значение путевой скорости W км/час устанавливается и отсчитывается по шкале 1 против индекса 
, если время берется в минутах или часах, либо против индекса 
, если время берется в секундах.
|
|
|
Шкалы 3 — синусы, 4 — тангенсы и 5 — радиусы разворота — расстояния — высоты предназначены для решения формул
S = Н tg α — на шкалах 4 и 5 (3)
и
S 1 = H sin α. — на шкалах 3 и 5, (4)
где S и S 1 — расстояние в м или км
Н — высота в м или км;
α — угол в град.
На неподвижной шкале 5 на корпусе линейки нанесены деления, соответствующие значению логарифмов чисел от 1 до 1000 (шкала 5 одинакова со шкалой 1), которые можно принимать за расстояния, высоты и радиусы разворота самолета в м или км. На движке нанесены логарифмы значений тангенсов углов от 0,5 до 85° (шкала 4) и логарифмы значений синусов углов от 5 до 90° или от 175 до 90° (шкала 3).
Шкала 6 является дополнительной и может использоваться совместно со шкалами 1, 2, 3, 4 и 5.
Она построена в 2 раза крупнее по масштабу, т, е имеет модуль М= 168 мм и ее деления соответствуют значениям логарифмов чисел от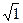 
до 
, т. е. являются корнями квадратными величин, нанесенных на шкалах 1 и 5. Шкала 6 служит для решения задач по определению радиуса разворота самолета, для извлечения корней квадратных из чисел и возведения их в квадрат, а также используется при решении комбинированных задач.
Шкалы 7 — сумма температур (t0 + tH), 8 — исправленная высота,
9 — высота по прибору и индекс 
служат для пересчета показаний барометрических высотомеров, построенных на принципе замера статического давления воздуха на высоте полета, в исправленное значение высоты с целью учета методической ошибки высотомера, являющейся следствием того, что фактическая средняя температура столба воздуха не совпадает с расчетной, принятой для построения шкалы высотомера по условиям международной стандартной атмосферы (МСА).
На верхней неподвижной шкале 7 нанесены логарифмы чисел, соответствующие сумме температур на земле и высоте полета (t0 + tH) в диапазоне от + 90 до—120°, это исключает ненужную операцию по определению средней температуры.
|
|
|
На шкале 8 на корпусе линейки нанесены логарифмы чисел, соответствующие исправленному значению высоты полета в диапазоне от 400 до 12000 м.
На подвижной шкале 9 (на движке) нанесены логарифмы величины ω, соответствующие значению высоты полета по прибору от 400 до 12000 м.
Шкалы 10 — температура для высоты более 11 000 м,
14 — исправленная высота и скорость,
15 — высота и скорость по прибору и индекс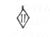 
служат для пересчета показаний барометрических высотомеров в исправленные значения высоты для высот более 12 000 м с целью учета методической ошибки, являющейся следствием того, что фактическая температура воздуха на высоте полета более 11 000 м не является постоянной и не равна расчетной 56,5°С, принятой для построения шкалы высотомера.
На верхней подвижной шкале 10 нанесены логарифмы чисел, соответствующие температуре на высоте полета в диапазоне от —30 до —75°С, и на шкале 14 (верхняя оцифровка шкалы) — логарифмы чисел, соответствующие исправленному значению высоты в диапазоне от 12 до 25 км. На нижней неподвижной шкале 15 нанесены логарифмы чисел, соответствующие значению высоты по прибору от 12 до 23 км (нижняя оцифровка). Установочный индекс 
совмещен с делением шкалы 12, равным 11 км. Кроме того, при пересчете высоты полета более 12 000 м по этим шкалам к значению высоты, отсчитанному по шкале 14, необходимо прибавить поправку ΔН = 900 + 20 (t0 + tH) со своим знаком.
Введение данной поправки вызвано тем, что фактическая высота слоя тропопаузы (т. е. высоты, с которой начинается постоянство температуры) для средних широт равна 9000—13 000 м и отличается от стандартной, которая принята для построения шкалы высотомера постоянной и равна 11 000 м.
Шкалы 11 — температура на высоте для скорости,
12 — высоты по прибору (км),
14 — исправленные высота и скорость,
15 — высота и скорость по прибору служат для пересчета показаний аэродинамических указателей скорости (типа УС-700.или УС-800), построенных на принципе измерения скоростного напора встречного потока воздуха, в исправленную скорость с учетом методической ошибки прибора из-за несоответствия фактической плотности воздуха на высоте расчетной плотности, по которой построена шкала прибора.
Шкалы 11 и 12 являются установочными, а шкалы 14 и 15 — основными, служащими для снятия отсчетов определяемых величин.
На шкале 11 (на движке) нанесены логарифмы величины τ, соответствующие значениям температуры воздуха на высоте от + 30 до — 70°С. На шкале 12 (неподвижная шкала на корпусе линейки) нанесены логарифмы величины Н, соответствующие высоте по прибору от 0 до 12 км, На шкале 14 нанесены логарифмы чисел, соответствующие исправленному значению скорости от 100 до 1400 км/час, а на шкале 15 — логарифмы чисел, соответствующие значению скорости по прибору от 100 до 1200 км/час. Пересчет скорости по этим шкалам выполняется без учета сжимаемости воздуха.
|
|
|
На рис. 8 показана схема решения задачи пересчета скорости по шкалам 11, 12, 14 и 15.
Шкала 13 — высоты по прибору (км) для КУС совместно со шкалами 11, 14 и 15 служит для пересчета показаний комбинированных указателей скорости (КУС) в исправленную скорость с учетом поправки на температуру из-за несоответствия фактического распределения температуры воздуха по высотам стандартным условиям распределения температуры, по которым построена шкала прибора.
В КУС, в отличие от обычных указателей скорости, с помощью анероидной коробки сообщается дополнительный поворот второй (тонкой) стрелке указателя скорости с поднятием на высоту. Этим вводится поправка на изменение плотности воздуха с высотой и поправка на сжимаемость с учетом плотности воздуха.
Шкала 16 служит для определения ошибок термометра наружного воздуха в полете вследствие нагревания его чувствительного элемента в заторможенном потоке или наличия трения о воздух. Величина поправки Δt зависит от истинной скорости полета и выражается формулой:
,
где V — истинная воздушная скорость в км/час;
0,265 — коэффициент пропорциональности.
По этой зависимости и построена шкала 16 (см. рис. 3).
При всех пересчетах высоты и скорости необходимо по этой шкале найти поправку Δ t и исправить показания термометров (типа ТУЭ или спиртового) по формуле, помещенной справа от шкалы:
| tИСПР= t –Δt |
Для термометров, замеряющих температуру воздуха при полном торможении, поправка выражается формулой
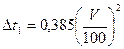
ИЛИ
,
таккак коэффициент 0,385 больше 0,265 приблизительно в 1,5 раза.
Умножение и деление чисел.
Для умножения и деления чисел используются шкалы 1 и 2 или 5 и 2, а также шкалы 14 и 15. Шкалы 1, 2 и 5 используются для умножения и деления в основном при решении специальных задач, связанных с расчетом скорости, высоты, времени полета и других навигационных элементов.
Шкалы 14 и 15 имеют деления с большим масштабом, и потому на них умножение и деление чисел можно выполнять с большей точностью (с большим числом значащих цифр).
При всех вычислениях на логарифмических шкалах необходимо знать и соблюдать следующие правила:
1. При отсчетах или установках по шкалам искомые или заданные числа можно увеличивать или уменьшать в 10,100 и т. д. раз.
2. В искомом результате важно правильно отделить число знаков (число цифр) слева от запятой. У десятичной дроби число знаков считается отрицательным и равным числу нулей справа от запятой до первой значащей цифры.
3. Число знаков произведения равно алгебраической сумме числа знаков множимого и множителя, если против множимого устанавливалось деление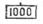 
шкалы 14 или 
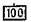шкалы 2 (движок вышел влево), или на единицу меньше, если против множимого было установлено деление 100 шкалы 14 или 
шкалы 2 (движок вышел вправо).
4. Число знаков частного равно алгебраической разности числа знаков делимого и делителя, если отсчет частного был сделан против деления 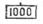шкалы 14 или 
шкалы 2 (движок вышел влево), или на единицу больше, если отсчет был сделан против деления 100 шкалы 14 или шкалы 2 (движок вышел вправо).
Подсчет и определение количества знаков при умножении и делении занимает некоторое время и требует запоминания правил. Чтобы избежать ошибок в определении количества знаков результата вычисления на линейке нужно грубо определить ответ в уме. Зная возможный порядок вычисляемых величин, можно всегда судить о количестве знаков результата, учитывая при этом размерность входных и исходных величин.
Порядок умножения (шкалы 14 и 15):
— передвигая движок, установить деление 100 или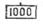 
на деление шкалы 15, соответствующее множимому (рис. 10);
— установить визирку по шкале 14 на деление, соответствующее множителю;
— отсчитать по визирке на шкале 15 искомое произведение.
Примеры: 1) 16,4 х 19,2 = 315.
Число знаков множимого 2, множителя 2, произведения (2+2) — 1 =3 (рис. 10, а).
2) 8,43 х 6,65 = 56.
Число знаков множимого 1, множителя 1, произведения (1 + 1)=2 (рис. 10, б).
3) 0,0065 х 3550 = 23,2.
Число знаков множимого —2, множителя +4, произведения (— 2 +4) = 2.
4) 0,125 х 0,214 = 0,0268.
Число знаков множимого 0, множителя 0, произведения (0+0) — 1= —1.
Порядок деления (шкалы 14 и 15):
— установить визирку по шкале 15 на деление, соответствующее делимому
— передвигая движок, подвести под визирку деление шкалы 14, соответствующее делителю;
— отсчитать по шкале 15 против деления 100 или 
искомое частное.
Примеры. 1) 181: 15,2 = 11,9.
Число знаков делимого 3, делителя 2, частного (3—2) + 1 = 2.
2) 67,5: 73 = 0,926.
Число знаков делимого 2, делителя 2, частного (2—2) = 0.
3) 0,0225: 0,0172 = 1,31.
Число знаков делимого —1, делителя —1, частного (-1)-(-1) +1 = 1.
4) 678: 0,73 = 927.
Число знаков делимого 3, делителя 0, частного (3+0) = 3.
Примечание. Порядок умножения и деления чисел на шкалах 1 и 2 отличается лишь тем, что вместо деления 100 и индекса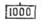 
шкалы 14 используются индексы и 
шкалы 2 соответственно.
ИЗВЛЕЧЕНИЕ КВАДРАТНЫХ КОРНЕЙ ИЗ ЧИСЕЛ И ВОЗВЕДЕНИЕ ИХ В КВАДРАТ.
Порядок решения (шкалы 5 и 6):
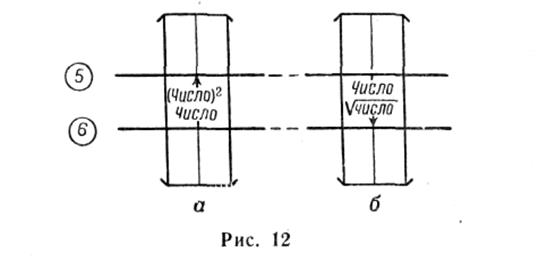
— установить визирку по шкале 6 на деление, соответствующее основанию степени, или по шкале 5 — на деление, соответствующее степени числа (рис. 12);
— отсчитать по визирке на шкале 5 искомое значение степени (квадрата числа) или по шкале 6 значение основания (корня квадратного из числа).
Примечания: 1. Число знаков квадрата числа равно удвоенному числу знаков основания, если квадрат числа отсчитывается на среднем интервале шкалы 5 (от 10 до 100); или на единицу меньше удвоенного, если отсчитывается на правом или левом интервалах (от 1 до 10 или от 100 до 1000).
2. Число знаков квадратного корня равно числу граней (включая и неполные), если подкоренное число больше или равно 1, или числу чисто нулевых граней, взятому со знаком минус, если подкоренное число меньше единицы; при этом «нуль целых» за грань не считается.
3. Квадратные корни с четным количеством знаков подкоренного выражения извлекаются по среднему интервалу шкалы 5 (10—100), с нечетным количеством знаков— по правому или левому интервалам шкалы 5 (100—1000 или 1—10).
4. Число, возводимое в квадрат, и значение подкоренного выражения можно увеличивать или уменьшать в 10, 100 и т. д. раз и соответственно в 102, 1002 и т. д. раз увеличивать или уменьшать результат.
Примеры:
1) 9,8122 = 96,3.
Число знаков результата (1 х 2) = 2.
2) 2,3522 = 5,52.
Число знаков результата (1 х 2) —1 = 1.
3) 17,622=309.
Число знаков результата (2 х 2) —1 = 3.
4). 
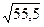=7,42.
Число граней 1, число знаков результата 1.
5). 
=16,8.
Число граней (неполных) 2, число знаков результата 2.
6). 
= 0,0807.
Число граней (нулевых) 1, число знаков результата —1.
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Определение значений синуса и тангенса заданного угла а (рис. 14)
производится по формулам
Порядок решения (шкалы 3, 4 и 5):
— передвигая движок, установить индекс 
на деление 100 шкалы 5 (рис. 15);
— установить визирку по шкале 4 на деление, соответствующее заданному углу, если находится тангенс и синус угла (угол меньше 5° или больше 175°), или по шкале 3, если находится синус угла (угол больше 5° или меньше 175°);
— отсчитать по визирке на шкале 5 (или 1) искомое значение синуса или тангенса угла, число значащих цифр зависит от цены деления данного участка шкалы и определяется интерполяцией последнего деления «на глаз».
Примечание.
Для определения значений косинусов и котангенсов углов необходимо визирку устанавливать по шкале 3 или 4 на значения дополнений углов до 90°, т. е. на значения (90°—α), где α — заданный угол.
Примеры: 1) sin45° = 0,70. 2) sinl5° = 0,26. 3) sinl73° = 0, 122. 4) tg56°=l,48.
5) tg25° = 0,467. 6) cos70° = sin20° = 0,341. 7) ctg21° = tg69° = 2,6.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ЧИСЛА НА ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛОВ
а) Умножение числа на синус и косинус угла:
a = b·sin a; d = b·cos a.
Порядок решения (шкалы 3 и 5):
— передвигая движок, установить индекс угла против деления шкалы 5, соответствующего числу (рис. 16 и 17);
— установить визирку по шкале 4 (если заданный угол меньше 5° или больше 175°) или по шкале 3 (если заданный угол больше 5° или меньше 175°) на деление, соответствующее заданному углу;
— отсчитать по визирке на шкале 5 искомое произведение.
Примечание.
Для умножения числа на значение косинуса угла необходимо устанавливать визирку на деление шкалы 3 или 4, соответствующее дополнению угла
до 90°, т. е. (90° — α).
Пример. Дано: b = 325; а = 28°.
Определить: α = 325 sin 28° = 152; d = 325 cos 28° = 325 sin 62° = 286.
б) Умножение числа на тангенс и котангенс угла
α = b tg α; d = b·ctg α.
Порядок решения (шкалы 4 и 5):
— передвигая движок, установить индекс 
против деления шкалы 5, соответствующего заданному числу (рис. 17);
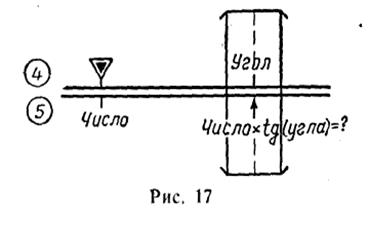
— установить визирку по шкале 4 на деление, соответствующее
заданному углу;
— отсчитать по визирке на шкале 5 искомое произведение.
Примечание.
Для умножения чисел на котангенс угла необходимо устанавливать визирку по шкале 4 на деление, соответствующее дополнению угла до 90°, т. е. (90° — α).
Пример. Дано: b = 15,4; а = 58°.
Определить: а = 15,4 tg 58° = 24,6; d = 15,4 ctg 58° = 15,4 tg 32° = 9,62.
|
|
|
