 |
3.2 Комплексные проницаемости
|
|
|
|
3. 2. 1 Основные соотношения
В переменных полях в линейном приближении вещество принято характеризовать двумя комплексными величинами — диэлектрической  и магнитной
и магнитной 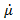 проницаемостями:
проницаемостями:
 ;
;  = μ ˊ - j μ ˊ ˊ
= μ ˊ - j μ ˊ ˊ
Действительные части этих величин описывают эффекты упругих взаимодействий полей с частицами вещества (ориентация, поляризация), а мнимые — тепловые потери всех видов (включая учет сквозной проводимости).
Сразу оговоримся: эти величины рассматриваются здесь чисто феноменологически, в первую очередь, с точки зрения измерений. Механизмы поляризации вещества, а также связь мнимой и действительной частей ε и μ обсуждаются, например, в [Сканави Г. И., физика диэлектриков (область слабых полей)].
В системе СИ вакууму также приписываются определенные значения 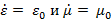 , которые в данном случае являются, по существу, действительными нормирующими коэффициентами; их иногда называют электрической и магнитной постоянными соответственно:
, которые в данном случае являются, по существу, действительными нормирующими коэффициентами; их иногда называют электрической и магнитной постоянными соответственно:
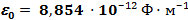 ,
,  = 1, 257 · 10− 6 Гн·
= 1, 257 · 10− 6 Гн· 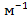
Через эти величины выражается мировая константа — скорость распространения электромагнитных волн в вакууме, а также соответствующая связь электрической и магнитной компонент поля в плоской волне:
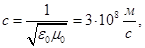
 ,
,
где W0 — волновое сопротивление свободного пространства.
На практике удобно оперировать относительными значениями  , поскольку влияние вещества на процессы электромагнитной природы определяются именно этими относительными величинами. Для сокращения записи индекс «r» часто опускают, при необходимости вводя абсолютные значения проницаемостей в виде
, поскольку влияние вещества на процессы электромагнитной природы определяются именно этими относительными величинами. Для сокращения записи индекс «r» часто опускают, при необходимости вводя абсолютные значения проницаемостей в виде  будем придерживаться такой традиции и приведем основные формулы, которые потребуются в дальнейшем.
будем придерживаться такой традиции и приведем основные формулы, которые потребуются в дальнейшем.
|
|
|
Комплексная проводимость конденсатора с металлическими электродами в диэлектрической среде
Y =  , (3. 2)
, (3. 2)
где 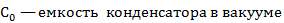
Примечание: формула (3. 2) приближенно справедлива и при заполнении диэлектриком только пространства между металлическими электродами; это тем более верно, чем расстояние между электродами меньше.
Комплексное сопротивление (импеданс) катушки в магнитной среде
Z =  , (3. 3),
, (3. 3),
где  - индуктивность катушки в вакууме.
- индуктивность катушки в вакууме.
Примечание: формула (3. 3) приближенно справедлива и в случае намотки катушки на магнитный сердечник (особенно тороидальный), если его размеры удовлетворяют определенным условиям. В общем же случае индуктивность катушки с сердечником зависит не только от магнитных свойств сердечника, но и от геометрических параметров последнего. К тому же определенное по (3. 3) значение  будет зависеть от тока в катушке.
будет зависеть от тока в катушке.
Волновое сопротивление среды c произвольными значениями относительных проницаемостей
W = 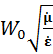 . (3. 4)
. (3. 4)
Используя (3. 5), электрическую и магнитную компоненты поля волны, распространяющейся вдоль оси z в однородном веществе или в заполненной таковым линии передачи с ТЕМ волной (Ez = Hz = 0), можно представить в виде
 (z) =
(z) =  exp (-j γ z),
exp (-j γ z),  (z) =
(z) =  (3. 5)
(3. 5)
где γ = 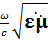 =
= 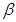 - j
- j  (постоянная распространения).
(постоянная распространения).
Связь электромагнитных волновых процессов со свойствами вещества будет, кроме (3. 4), определяться двумя скалярными величинами:
постоянной фазы β =  Re
Re  , (3. 6)
, (3. 6)
постоянной затухания  =
=  Im
Im  , (3. 7)
, (3. 7)
Здесь  — круговая частота, с — скорость света в свободном пространстве.
— круговая частота, с — скорость света в свободном пространстве.
 Иногда удобно использовать другие, производные, величины, также зависящие от
Иногда удобно использовать другие, производные, величины, также зависящие от  :
:
Фазовая скорость v=  , соответственно, длина волны в веществе определится как
, соответственно, длина волны в веществе определится как
 (3. 8)
(3. 8)
Коэффициент затухания Г= 8. 686  [дБ/м]. (3. 9)
[дБ/м]. (3. 9)
|
|
|
Все эти параметры относятся к волнам в бесконечном пространстве или в однородной линии бесконечной длины. Реальные же системы всегда конечны, что заставляет считаться с процессами, происходящими с волнами при прохождении границ раздела двух сред или стыка линий с разными волновыми сопротивлениями. Поэтому к перечисленным параметрам надо добавить еще два:
Коэффициент отражения (комплексный, по напряжению или полю Е) на стыке линий с разными значениями W или в пространстве при нормальном падении волн на границу из среды с W1 в среду c W2 (см. рис. 3. 6):
p = -  (3. 10)
(3. 10)
Важное замечание: фаза коэффициента отражения может меняться в пределах от нуля до – π в зависимости от соотношения волновых сопротивлений. Коэффициент отражения от идеального проводника (металла), как и от закороченной линии, равен -1. Если же конец линии разомкнут, то р = 1.
Коэффициент прохождения (комплексный) определится формулой
Т =  , (3. 11)
, (3. 11)
Выражение (3. 9) следует из условия равенства касательных компонент электрического поля с обеих сторон границы, то есть
1+p  = T (3. 12)
= T (3. 12)
Амплитуда прошедшей волны при этом определится из условия баланса мощностей как
|T| =  , (3. 13)
, (3. 13)
|
|
|


