 |
Волновые методы (ВМ)
|
|
|
|
Если требующиеся размеры цепи уже нельзя считать много меньшими длины волны (ориентировочным критерием здесь можно считать 0. 05λ ), следует от цепей с сосредоточенными параметрами переходить к цепям с параметрами распределенными.
Методы измерения, основанные на использовании таких цепей, можно назвать волновыми, поскольку в их основе лежит рассмотренная в разделе 3. 2. 1 связь характеристик волновых процессов в пространстве или линиях передачи с параметрами сред, в которых эти процессы происходят.
Отметим одно практически важное приближение – случай малых потерь, когда ε ˊ ˊ ˂ ˂ ε ˊ, то есть tgd ˂ ˂ 1. Тогда, с точностью до величин порядка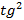 
d, можно считать, что:
(3. 15)
Im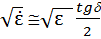 
Это значит, что, если потери достаточно малы, действительную часть КДП можно измерять только по величинам, определяемым постоянной фазы β (например, по длине волны в веществе или задержке).
Существенно (и это особенность волновых процессов), что во все приведенные формулы КДП входит только под корнем, как 
; в оптике величина называется коэффициентом преломления и обычно обозначается буквой n. Но для большинства применений и требуется знать именно 
! Поэтому оценивать точность измерения самой 
имеет смысл, только если речь идет о справочных данных или расчете емкостей.
Все варианты практической реализации волновых методов измерения КДП основаны на использовании приведенных в 3. 2. 1 соотношений. Выбор конкретного варианта зависит, в первую очередь, от того, в каком виде оказывается доступным исследуемое вещество. Ограничимся рассмотрением нескольких распространенных ситуаций:
|
|
|
Ситуация 1. Исследуемым веществом возможно заполнить ячейку в виде отрезка линии передачи (жидкости, порошки, специально изготовленные образцы). Общая схема ячейки приведена на рис. 3. 11, а примеры реализации - на рис. 3. 12.
Рис. 3. 11
Рис. 3. 12. (а): Коаксиальная ячейка, использовавшаяся для исследования свойств полимеров в диапазоне частот 1 ГГц – 5 ГГц. Образцы – цилиндрические шайбы высотой 7 мм, соответствующие внутренним размерам ячейки. (б): Плоскопараллельная ячейка с диаметром внутреннего проводника 2 мм, применявшаяся для исследования КДП цемента (в том числе в процессе схватывания) на частотах 1ГГц – 4ГГц. ( добавить буквы на рисунок! ),
Измерительная ячейка, как видно, представляет собой симметричный четырехполюсник с СВЧ разъемами для включения в измерительную схему. С помощью векторного анализатора цепей (ВАЦ) и подобных ячеек можно получать экспериментальные зависимости комплексных элементов матрицы рассеяния (S11 и S21) от частоты. Посмотрим, как эти данные могут использоваться для определения КДП.
Прежде всего, заметим, что измерительная ячейка в виде отрезка линии с разъемами на концах позволяет использовать четыре схемы измерений, отличающиеся состоянием выходного (правого) конца:
- короткое замыкание, (двухполюсник, измерение S11)
- холостой ход, (двухполюсник, измерение S11)
- нагрузка Z, обычно равная W1, (двухполюсник, измерение S11)
- измерительный тракт с W=W1. (четырехполюсник, измерение S11и/или S21)
Кроме того, длина образца может составлять как малые доли длины волны, так и десятки длин волн.
Экспериментатор не всегда имеет возможность выбирать тот или иной вариант схемы, но должен понимать особенности каждой из них. Например, при малых потерях в веществе разумно выбирать двухполюсные схемы, при больших – четырехполюсные, при работе с жидкостями удобнее всего использовать короткозамкнутую ячейку и располагать ее вертикально.
|
|
|
Рассмотрим примеры.
На рис. 3. 13 приведены реальные данные измерений (модули S21 в дБ) в интервале частот 0. 1 – 2. 5 ГГц для двух образцов бетона в процессе затвердевания [Измерение электрофизических параметров бетона в диапазоне 100-2500 МГц, Попов И. Б., выпускная работа бакалавра, Санкт-Петербург, Санкт-Петербургский Политехнический университет, 2004].
Рис. 3. 13. Данные для двух образцов бетона в процессе затвердевания
Попробуем проанализировать их и сказать что-либо о КДП бетона.
1. Зависимость модуля S21 на 10-й день (верхние кривые, сухой бетон) имеет осциллирующий характер; он обусловлен интерференцией прямой волны и волн, претерпевших многократные отражения. А если так, то число периодов в этой зависимости должно быть связано с электрической длиной ячейки, а значит, и с ε.
Действительно, нетрудно установить, что приближенно справедливо удобное для оценок соотношение
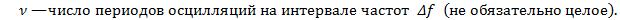
Отсюда для данного случая получаем 
1. 8, или 
С другой стороны, средний уровень рассматриваемой зависимости с частотой линейно уменьшается (линейная регрессия), что, естественно, связано с затуханием волн, то есть со значением tgd или ε ˊ ˊ. Учитывая, что график модуля S21 приведен в логарифмическом масштабе, получаем:
где b — коэффициент наклона, дБ/Гц.
Рис. 3. 14 Крайние случаи для образца №1 с линиями линейной регрессии
В данном случае b = 0. 083 * 
Отсюда, с учетом , получаем tgd @ 0. 11. Как видно, пока удалось обойтись только значениями модуля S21.
2. Теперь обратимся к нижним кривым на рис. 3. 13 и 3. 14 (влажный бетон). Эти зависимости уже не имеют заметных осцилляций, что говорит о существенно большем затухании волн (даже двукратно отраженные волны не влияют на результат).
Величину 
tgd здесь можно определить, как и раньше, через средний коэффициент наклона (считая функцию линейной). Но вот просто оценить значение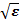 
по зависимости модуля S21 от частоты не удастся. Здесь потребуются либо измерения фазы этой величины, либо, что предпочтительней, действительной или мнимой ее компоненты (все современные ВАЦ имеют режимы индикации «Re» и «Im»). Легко показать, что в общем случае эти компоненты будут содержать синусоидальные составляющие с аргументами вида Δ ω · 
, где величины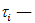 
задержки волн, соответствующие различным путям, проходимых ими в веществе, а Δ ω — диапазон перестройки частоты. Если же рассматривать только прямой путь через ячейку длиной 15 см, то t будет равно 0. 15 
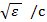и при изменении частоты на 2. 4 ГГц получим зависимость с «частотой» ν, равной 1. 2 
. Таким образом, если ν оказалась равной, например, 3. 5 то ε определится как 8. 5.
|
|
|
Замечание. Приведенные примеры имеют существенное различие. В первом случае осцилляции модуля S21 при изменении частоты не зависят от калибровки прибора по фазе, поскольку определяются только ячейкой (интерферируют волны, прошедшие ячейку один и три раза). Во втором же примере подразумевается, что отсчет фазы ведется от левого края ячейки. Поэтому без диэлектрика, то есть при ε = 1, получаем ν = 1. 2. Условия калибровки по фазе меняют значение ν.
Оценки, подобные приведенным, можно получить и для двухполюсных схем измерения (с ХХ и КЗ на правом конце).
Еще лет тридцать тому назад здесь следовало бы детально рассмотреть те схемы и частные случаи, для которых возможно получить приемлемые по точности и сложности расчетные формулы для нахождения компонент КДП по данным измерений (то есть решить обратную задачу). Примерами такого подхода могут служить методы Николсона-Росса-Вейра (NRW), NIST Iterative метод, New non-iterative метод. Ниже приведен отрывок из [ ], содержащий краткие характеристики этих методов.
«Метод Николсона-Росса-Вейра (NRW) позволяет прямым расчётом вычислить как диэлектрическую, так и магнитную проницаемости с помощью измеренных S− параметров. Это наиболее широко используемый метод, выполняющий такое преобразование. Данный метод расчёта подразумевает, что все S− параметры (𝑆 11, 𝑆 21, 𝑆 12, 𝑆 22) или пара (𝑆 11, 𝑆 21) S− параметров найдены экспериментально. Однако метод расходится для материалов с низкими потерями на частотах, соответствующих половине длины волны в образце, что обусловлено неоднозначностью фазы. Следовательно, оно ограничено оптимальной толщиной образца 𝜆 /2 и предпочтительно его использовать для образцов малой толщины.
|
|
|
NIST Iterative метод (NIST) позволяет выполнять расчёт диэлектрической проницаемости методом поиска корней Ньютона-Рафсона. Этот метод использует все четыре S-параметра (𝑆 11, 𝑆 21, 𝑆 12, 𝑆 22) или пару (𝑆 11, 𝑆 21) S-параметров исследуемого образца для расчёта коэффициентов отражения и пропускания. Он хорошо работает, если задаться хорошим начальным значением. Метод устраняет неточности, которые существуют в методе Никольсона-Росса-Вейра, когда толщина образца является целым числом, кратное половине длине волны (𝑛 𝜆 𝑔 /2). Он подходит для длинных образцов и позволяет исследовать материалы с низкими потерями. На
New non-iterative метод очень похож на NRW метод, но он применим только для расчета диэлектрической проницаемости при магнитной проницаемости 𝜇 𝑟 = 1. Этот метод использует все четыре (S11, S21, S12, S22) или только два (S11, S21) S-параметра исследуемого образца для вычисления коэффициентов отражения и передачи. Преимущество метода заключается в том, что он является стабильным во всем диапазоне частот для произвольной толщины образца. Метод основан на упрощенной версии метода Никольсона-Росса-Вейра и не наблюдается расхождения на частотах, соответствующих половине длины волны в образце. Он не требует первоначальной оценки диэлектрической проницаемости и может очень быстро выполнять расчет. Точность измерения сопоставима с итерационным методом. Данный метод можно легко распространить на микрополосковые или копланарные линии измерения»
Сейчас, однако, роль такого рода методов существенно уменьшилась, поскольку любая из рассмотренных схем легко моделируется численно в современных пакетах (HFSS, CST, и даже в MathCad). Наличие же несложной цифровой модели позволяет быстро решать обратную задачу методом вариации ее параметров до получения совпадения результатов моделирования с результатами эксперимента. Привлекательными свойствами такого метода являются:
- возможность учета реальных особенностей условий эксперимента (например, в модели легко учесть зазоры, прокладки и т. п. детали, влияние которых на результат очень трудно оценить аналитически)
- возможность быстрого выявления дефектов реализованной измерительной схемы: при их наличии приблизить смоделированные характеристики к полученным экспериментально не удается, и это видно с первых же итераций.
|
|
|
- возможность использовать одну и ту же базовую модель ячейки для работы со всеми четырьмя вариантами измерительных схем
- весьма высокая чувствительность к задаваемым параметрам (см. расчетные примеры на рис. 3. 15).
Рис. 3. 15. Чувствительность модели к вариациям параметров вещества
Пример использования метода моделирования в задаче определения КДП полимеров с включениями нанопоршков приведен на рис. 3. 16 и 3. 17. (использовалась ячейка, показанная на рис. 3. 11)
Рис. 3. 16 Эксперимент: модуль и фаза S21 в диапазоне 1 – 5 ГГц на экране VNA HP8510B
Рис. 3. 17 Модель: те же характеристики при подобранных параметрах вещества
Пример результата измерений партии образцов:
установлено, что
– для полимерной матрицы в диапазоне 1ГГц – 5 ГГц параметры диэлектрика практически постоянны (ε = 2. 6 + 0. 1, tg δ = 0. 015 + 0. 05).
- введение наночастиц увеличивает значения диэлектрической проницаемости до 4. 2 +0. 1, которая также мало меняется в указанном диапазоне, а значения tg δ плавно увеличиваются с частотой от 0. 02 до 0. 08.
Примечание. В этих измерениях могла быть достигнута и большая точность, однако она не требовалась.
Еще один пример соответствия модели линии (в данном случае копланарной) и экспериментальных данных:
Рис. 3. 18 Копланарная ячейка: модельные и реальные характеристики
Ситуация 2 . Вещество представлено образцом простой формы (сфера, цилиндр, тороид…)
Для этих образцов удобно использовать метод, основанный на определении частоты резонанса одной из мод (обычно низшей) колебаний в образце. Так, для немагнитной диэлектрической сферы радиуса R положение первого резонанса может быть определено из соотношения 
[Д. С. Филонов, А. П. Слобожанюк, П. А. Белов, ТЕХНОЛОГИИ И ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ В РАДИОФИЗИКЕ И ТОМОГРАФИИ, Методические указания к лабораторному практикуму, Санкт-Петербург, ИТМО, 2020].
Возбуждение при этом производится внешним полем, для создания которого могут использоваться разные устройства - антенны, полые волноводы, малые рамки. Для получения резонансного отклика здесь необходимо лишь наличие у источника компоненты поля, соответствующей структуре поля используемой моды (рис. 3. 19).
А В
Рис. 3. 19 А - тороидальный керамический образец в поле широкополосной антенны (образец закреплен на стержне из сухого дерева), В – коэффициент отражения антенны с образцом (S11)
Но в общем случае резонансная частота и, тем более, ширина резонансной кривой, могут быть связаны с компонентами комплексной диэлектрической проницаемости весьма сложным образом. Простые соотношения, подобные приведенному выше, справедливы лишь в пренебрежении влиянием конструктивных элементов источника на объект и излучением последнего. Поэтому для корректного определения значений ε и tgd рассмотренным методом необходимо экспериментальные результаты сопоставлять с весьма полным математическим моделированием измерительной схемы.
|
|
|
