 |
Важное замечание: из 3.12 следует, что фаза прошедшей волны мало отличается от фазы волны, падающей даже при относительно больших значениях модуля р.
|
|
|
|
Важное замечание: из 3. 12 следует, что фаза прошедшей волны мало отличается от фазы волны, падающей даже при относительно больших значениях модуля р.
Приведенных соотношений достаточно для разработки и обоснования большинства методов измерения параметров веществ и материалов (как электрических, так и магнитных) на радиочастотах.
Действительно, компоненты постоянной распространения a и β , а также комплексный коэффициент отражения р принципиально можно измерить в эксперименте (например, используя отрезок линии передачи), а коль скоро они известны, то из (3. 6) и (3. 7) легко находится величина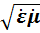 
, а из (3. 4 и з 3. 10) – 
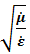. Дальнейшие действия по определению 
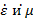тривиальны.
Чаще всего, однако, приходится иметь дело с диэлектриками, являющимися диамагнетиками или парамагнетиками; при этом ничтожное отличие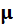 
от единицы не является значимым и может не приниматься во внимание. Кроме того, магнитные свойства веществ на радиочастотах и их определение имеют свою специфику, уделить должное внимание которой в данном курсе нет возможности (см., например. Микаэлян А. Л. Теория и применение ферритов на сверхвысоких частотах. 1963).
По этим причинам в дальнейшем сосредоточимся на диэлектрических свойствах веществ, полагая их немагнитными, то есть будем считать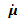 
=1.
3. 2. 2 Измерение комплексной диэлектрической проницаемости (КДП)
Метод конденсатора (МК)
Проводимость идеального конденсатора на переменном токе частотой ω записывается как
Y = jB = jω C = jω ε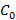 
,
где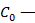 
емкость конденсатора без диэлектрика, а ε — действительная величина.
При замене ε на 
, в соответствии с (3. 2), получим
Y = j ω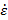 
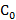= j ω ε ˊ 
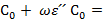ReY + j ImY = G + jB,
|
|
|
откуда
ε ˊ =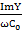 
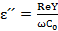, tg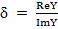 
. (3. 14)
Таким образом, для определения КДП вещества, заполняющего конденсатор, достаточно (зная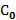 
) измерить действительную и мнимую части его проводимости на частоте ω.
Такие измерения удобно проводить, используя векторный анализатор цепей и круговую диаграмму проводимостей - функцию «Inverse Smith»:
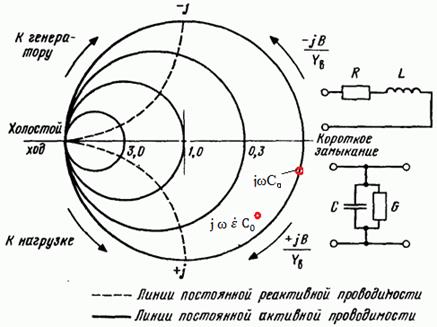
Рис. 3. 6 Диаграмма проводимостей « Inverse Smith»
Для реализации МК (чаще всего, на частотах до десятков мегагерц) могут использоваться конденсаторные ячейки различной формы, например, цилиндрические. На изменении параметров конденсатора в зависимости от КДП заполняющего его вещества основаны и разнообразные автогенераторные методы (используется зависимость частоты генерируемого сигнала от емкости в резонансной системе).
Внимание!
Используя МК, следует иметь в виду ряд тонкостей, влияющих на точность измерений:
Краевые эффекты . Приведенные соотношения справедливы при сравнении параметров конденсатора в свободном пространстве с тем же конденсатором, полностью погруженным в исследуемое вещество. Если же веществом заполняется только пространство между электродами, то расстояние d между ними должно быть много меньшим минимального размера электродов; в противном случае роль краевых эффектов будет значительной. Более точные оценки для конкретных случаев (в том числе для цилиндрических конденсаторов) могут быть получены путем математического моделирования.
Частота. Основное ограничение — электрические размеры конденсатора должны быть много меньшими длины волны (с умножением на корень из максимального ожидаемого значения ε, см. далее). Даже для оценочных измерений не рекомендуется использовать конденсаторные ячейки размером более 0. 1 длины волны и с расстоянием d более 0. 01 длины волны.
Перечисленные эффекты препятствуют непосредственному использованию МК на СВЧ (хотя бы уже потому, что корректно реализовать заполняемый веществом измерительный конденсатор размерами в несколько миллиметров достаточно сложно).
|
|
|
Интересное исключение здесь представляет метод открытого конца коаксиальной линии (Open Ended Coaxial Line Method, OECP, ОККЛ) [см. вставку ниже, дать ссылку],
который в некоторых вариантах может использоваться даже на частотах до десятков гигагерц. Здесь в качестве эталонной емкости используется торцевая емкость открытого конца коаксиальной линии, составляющая для 50-омных линий величину порядка 0. 1 пф.
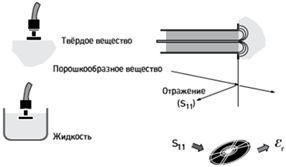
Рис. 3. 7 Метод ОККЛ
Примером реализации метода ОККЛ может служить набор датчиков DAK (Dielectric Assessment Kit) фирмы Speag [.. ], см. рис. 3. 8.
Рис. 3. 8 Фирменный набор датчиков DAK
Следует, однако, отметить, что вполне работоспособные датчики для метода ОККЛ могут быть изготовлены и самостоятельно из подходящего кабеля и /или коаксиальных разъемов (рис. 3. 9 и 3. 10). Такие датчики и некоторый опыт их калибровки с помощью материалов с известными и стабильными диэлектрическими свойствами (например, тефлона), позволяют легко проводить измерения КДП в любых условиях, располагая только подходящим ВАЦ (желательно с функцией «Inverse Smith»).
Рис. 3. 9. Емкостной датчик из жесткого коаксиального кабеля диаметром 1 мм (применялся для исследования тонких (1. 5 мм) плоских образцов полимеров на частотах до 20 ГГц)
Рис. 3. 10 Емкостной датчик из приборного проходного разъема SMA; использовался для измерений параметров листовых радиопоглощающих материалов (РПМ) на частотах до 1 ГГц -5 ГГц.
Главные достоинства метода ОККЛ – отсутствие необходимости в изготовлении специальных образцов и возможность оперативность применения. Метод обеспечивает достаточную для практических целей точность, если толщина образца будет больше, чем внутренний диаметр коаксиальной линии. К общим же его недостаткам следует отнести трудности использования на частотах ниже 100 МГц (из-за малой исходной емкости торца линии) и ограничения со стороны малых значений tgd (из-за наличия собственного излучения, зависящего, к тому же, не только от КДП вещества, но и от формы диэлектрического образца). Для коррекции данных с учетом этих факторов в широких частотных диапазонах фирмы применяют специальное ПО и сложные процедуры калибровки.
|
|
|
Рекомендация : при использовании самодельных датчиков калибровку и измерения лучше производить на фиксированных частотах. Если конкретное значение частоты не имеет принципиального значения, то, по крайней мере при оценочных измерениях, удобно выбрать его из условия ω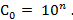 
Что при этом получится, видно из формулы (3. 3).
|
|
|
