 |
Распределение напряжений при действии равномерно распределенной нагрузки по полосе (по подошве ленточного фундамента).
|
|
|
|
Для практических расчетов ленточным считается фундамент (штамп) при соотношении сторон  .
.

Напряжения на горизонтальных площадках в точке М на глубине z ниже подошвы полосы определяется:

Напряжения на вертикальных площадках в точке М на глубине z определяется:

Для практических расчетов напряжений  под полосовой нагрузкой принимается табличный метод, аналогично как для прямоугольных фундаментов с использованием таблицы 10.2 для определения коэффициентов
под полосовой нагрузкой принимается табличный метод, аналогично как для прямоугольных фундаментов с использованием таблицы 10.2 для определения коэффициентов 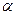 под центром полосовой нагрузки (
под центром полосовой нагрузки ( ).
).
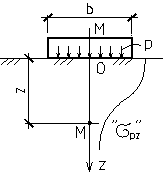
Случай 1. Ось М-М расположена по средине полосовой нагрузки: ( ).
).
| 
|
Случай 2. Ось М-М проходит внутри контура полосовой нагрузки ( ).
).
Через точку М проводится линия, разделяющая полосу на две шириной  и
и 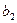 , для которых она лежит на контуре. Напряжение от каждой условно
, для которых она лежит на контуре. Напряжение от каждой условно

| выделенной полосы составляет:

|
 принимаются по табл.10.2 при
принимаются по табл.10.2 при  .
.
Случай 3. Ось М-М проходит за контуром полосовой нагрузки.
Через точку М производится построение полосы шириной  и
и 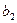 . Загружение полосы
. Загружение полосы  принимается со знаком плюс «+», полосы шириной
принимается со знаком плюс «+», полосы шириной 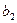 со знаком минус «-».
со знаком минус «-».

| 
|
 принимаются по табл.10.2 при
принимаются по табл.10.2 при  .
.
Для определения суммарного влияния полосовой нагрузки на изменение напряжений  по глубине и простиранию можно воспользоваться таблицей 10.3
по глубине и простиранию можно воспользоваться таблицей 10.3
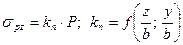 ,
,
где 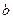 - ширина полосы;
- ширина полосы;  и
и  - глубина и удаление рассматриваемой точки от центра полосы.
- глубина и удаление рассматриваемой точки от центра полосы.
Таблица 10.3
Коэффициент (kn) изменения давлений в толще грунта (σpz) от полосовой нагрузки интенсивностью σpzо=1
| ζ c=z/b | Величины коэффициента кn при удалении J/b равном | |||||||
| 0,25 | 0,50 | 0,70 | 1,0 | 1,30 | 1,60 | 2,0 | ||
| 1,0 | 1,0 | 0,50 | ||||||
| 0,2 | 0,9773 | 0,9368 | 0,4984 | 0,0899 | 0,0109 | 0,0028 | 0,0010 | 0,0004 |
| 0,4 | 0,8810 | 0,7971 | 0,4886 | 0,2182 | 0,0558 | 0,0181 | 0,0074 | 0,0029 |
| 0,6 | 0,7554 | 0,6792 | 0,4684 | 0,2818 | 0,1110 | 0,0451 | 0,0206 | 0,0086 |
| 0,8 | 0,6417 | 0,5856 | 0,4405 | 0,3069 | 0,1553 | 0,0758 | 0,0388 | 0,0176 |
| 1,0 | 0,5498 | 0,5105 | 0,4092 | 0,3114 | 0,1848 | 0,1037 | 0,0585 | 0,0289 |
| 1,2 | 0,4774 | 0,4498 | 0,3777 | 0,3050 | 0,2018 | 0,1257 | 0,0771 | 0,0412 |
| 1,4 | 0,4200 | 0,4004 | 0,3480 | 0,2931 | 0,2097 | 0,1415 | 0,0931 | 0,0534 |
| 1,6 | 0,3741 | 0,3597 | 0,3209 | 0,2789 | 0,2115 | 0,1518 | 0,1059 | 0,0647 |
| 1,8 | 0,3367 | 0,3260 | 0,2965 | 0,2639 | 0,2094 | 0,1579 | 0,1155 | 0,0746 |
| 2,0 | 0,3058 | 0,2976 | 0,2749 | 0,2492 | 0,2047 | 0,1606 | 0,1222 | 0,0828 |
| 2,5 | 0,2481 | 0,2436 | 0,2309 | 0,2159 | 0,1884 | 0,1586 | 0,1299 | 0,0986 |
| 3,0 | 0,2084 | 0,2057 | 0,1979 | 0,1886 | 0,1707 | 0,1502 | 0,1292 | 0,1028 |
| 3,5 | 0,1795 | 0,1777 | 0,1727 | 0,1665 | 0,1544 | 0,1400 | 0,1245 | 0,1038 |
| 4,0 | 0,1575 | 0,1563 | 0,1529 | 0,1486 | 0,1401 | 0,1297 | 0,1181 | 0,1020 |
| 4,5 | 0,1403 | 0,1395 | 0,1370 | 0,1339 | 0,1277 | 0,1200 | 0,1112 | 0,0986 |
| 5,0 | 0,1265 | 0,1259 | 0,1240 | 0,1218 | 0,1171 | 0,1113 | 0,1045 | 0,0945 |
| 5,5 | 0,1151 | 0,1146 | 0,1133 | 0,1115 | 0,1080 | 0,1034 | 0,0981 | 0,0902 |
| 6,0 | 0,1056 | 0,1052 | 0,1042 | 0,1028 | 0,1001 | 0,0965 | 0,0922 | 0,0858 |
|
|
|

Распределение напряжений при действии равномерно распределенной нагрузки по площади прямоугольного треугольника.

|
Ось М-М проходит через одну из вершин острых углов треугольника, b – катет меньшей длины; l – катет большей длины;  - острый угол.
Напряжение по оси М-М на глубине z предлагается определить табличным способом: - острый угол.
Напряжение по оси М-М на глубине z предлагается определить табличным способом:
 Величины коэффициентов распределения напряжений
Величины коэффициентов распределения напряжений 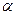 приведены в таблице 10.4. приведены в таблице 10.4.
|
Таблица 10.4
Величины коэффициентов 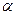 при угле при угле 
| |||||||

| Отношение катетов треугольников 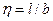
| ||||||
| 1,4 | 1,8 | 2,4 | 3,2 | ≥10 | |||
| 0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8 5,2 5,6 6,0 6,4 6,8 7,2 7,6 8,4 9,2 10,0 11,0 12,0 | 0,125 0,120 0,100 0,076 0,056 0,042 0,032 0,025 0,020 0,016 0,013 0,011 0,010 0,008 0,007 0,006 0,006 0,005 0,004 0,004 0,003 0,003 0,002 0,002 0,002 | 0,151 0,146 0,124 0,096 0,073 0,055 0,043 0,034 0,027 0,022 0,018 0,015 0,013 0,011 0,010 0,009 0,008 0,007 0,006 0,006 0,005 0,004 0,003 0,003 0,002 | 0,169 0,164 0,141 0,111 0,086 0,066 0,052 0,041 0,034 0,028 0,023 0,020 0,017 0,014 0,013 0,011 0,010 0,009 0,008 0,007 0,006 0,005 0,004 0,004 0,003 | 0,187 0,181 0,158 0,127 0,100 0,079 0,063 0,051 0,042 0,035 0,029 0,025 0,022 0,019 0,016 0,015 0,013 0,011 0,010 0,009 0,008 0,007 0,006 0,005 0,004 | 0,202 0,196 0,172 0,141 0,113 0,091 0,074 0,061 0,051 0,043 0,036 0,031 0,027 0,024 0,021 0,019 0,017 0,015 0,013 0,012 0,010 0,009 0,007 0,006 0,005 | 0,219 0,213 0,189 0,158 0,129 0,106 0,089 0,075 0,063 0,056 0,047 0,041 0,037 0,032 0,029 0,026 0,023 0,021 0,019 0,017 0,015 0,013 0,011 0,009 0,008 | 0,234 0,228 0,204 0,173 0,145 0,122 0,104 0,089 0,078 0,069 0,061 0,055 0,049 0,045 0,041 0,038 0,035 0,032 0,030 0,028 0,024 0,022 0,020 0,018 0,015 |
Величины коэффициентов 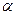 при угле при угле 
| |||||||
| 0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8 5,2 5,6 6,0 6,4 6,8 7,2 7,6 8,4 9,2 10,0 11,0 12,0 | 0,125 0,120 0,100 0,076 0,056 0,042 0,032 0,025 0,020 0,016 0,013 0,011 0,010 0,008 0,007 0,006 0,006 0,005 0,004 0,004 0,003 0,003 0,002 0,002 0,002 | 0,099 0,097 0,088 0,075 0,060 0,048 0,038 0,031 0,025 0,021 0,018 0,015 0,013 0,011 0,010 0,009 0,008 0,007 0,006 0,005 0,005 0,004 0,003 0,003 0,002 | 0,081 0,080 0,076 0,068 0,059 0,050 0,041 0,035 0,029 0,024 0,021 0,018 0,016 0,014 0,012 0,011 0,010 0,008 0,008 0,007 0,006 0,005 0.004 0,004 0,003 | 0,063 0,063 0,061 0,058 0,053 0,047 0,042 0,036 0,032 0.028 0,024 0,021 0,019 0,016 0,015 0,013 0,012 0,011 0,010 0,009 0,007 0,006 0,005 0,005 0,004 | 0,048 0,048 0,048 0,046 0,044 0,041 0,038 0,035 0,032 0,028 0,026 0,023 0,021 0,019 0,017 0,015 0,014 0,013 0,012 0,011 0,009 0,008 0,007 0,006 0,005 | 0,031 0,031 0,031 0,031 0,031 0,030 0,029 0,028 0,027 0,025 0,024 0,023 0,021 0,020 0,018 0,017 0,016 0,015 0,014 0,013 0,012 0,010 0,009 0,008 0,007 | 0,016 0,016 0,016 0,016 0,016 0,016 0,016 0,016 0,015 0,015 0,015 0,015 0,015 0,015 0,015 0,014 0,014 0,014 0,014 0,013 0,013 0,012 0,012 0,011 0,011 |
|
|
|
При необходимости более точного определения напряжений при давлениях равномерно распределенных по площади прямоугольных треугольников с другим соотношением сторон, принимается 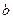 - катет, прилежащий к вершине острого угла;
- катет, прилежащий к вершине острого угла;  - катет противолежащий
- катет противолежащий

Для практических расчетов напряжения под вершинами в острых углах прямоугольных треугольников с промежуточным соотношением сторон определяются интерполяцией по таблице 10.4.
Напряжения на оси, проходящей через прямой угол треугольника, определяются как сумма напряжений от 2-х прямоугольных треугольников,

| образуемых высотой, опущенной из прямого угла

 - определяются по табл.10.4. - определяются по табл.10.4.
|
Распределение напряжений от собственного веса грунта.
Случай 1. Основание представлено одним слоем однородного грунта с постоянным весом по глубине ( ), грунтовые воды отсутствуют.
), грунтовые воды отсутствуют.

| 
|
Случай 2. Основание по глубине представлено несколькими слоями грунта, удельные веса каждого грунтового слоя неизменны, грунтовые воды отсутствуют.

| 
|
|
|
|
Случай 3. В грунтовом основании, представленном однородным слоем, имеются грунтовые воды, грунт взвешивается  .
.
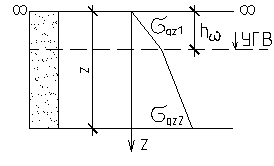
| К расчету принимается двухслойное основание

|
Случай 4. Слоистое грунтовое основание ниже грунтовых вод представлено слоями грунтов, испытывающих ( ) и не испытывающих (
) и не испытывающих ( ) взвешивающее действие воды.
) взвешивающее действие воды.

| 
 - определяется при полном водонасыщении ( - определяется при полном водонасыщении ( ) )
|
|
|
|



 - удельный вес грунта с учетом взвешивающего действия воды.
- удельный вес грунта с учетом взвешивающего действия воды.