 |
Примеры вычисления по распределению напряжений в массиве грунта. Нагружение грунта обеспечивается в интервале применимости теории линейно деформируемых тел.
|
|
|
|
Пример 1.
На поверхности грунта установлен штамп с размерами в плане 2,5х4м, который передает давление  . Определить величины сжимающих напряжений по горизонтальным площадкам (
. Определить величины сжимающих напряжений по горизонтальным площадкам ( ) по вертикальной оси, пересекающей поперечную ось симметрии на расстоянии 2,5м от центра тяжести площади загружения. Расчеты выполнить с применением решения задачи о действии сосредоточенной силы.
) по вертикальной оси, пересекающей поперечную ось симметрии на расстоянии 2,5м от центра тяжести площади загружения. Расчеты выполнить с применением решения задачи о действии сосредоточенной силы.


| Решение:
Площадь прямоугольника загрузки разбивается на 4-е прямоугольника с размерами 
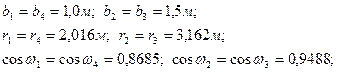 Принимаем изменение глубины по оси М1 с шагом
Принимаем изменение глубины по оси М1 с шагом  .
Расчеты приведены в таблице: .
Расчеты приведены в таблице:
|
Пример 2.
Поверхность грунта загружена на площади 2,5х4,0м равномерно распределенной нагрузкой  . Определить величины сжимающих напряжений (
. Определить величины сжимающих напряжений ( ) по осям, проходящим через: центр загруженной площади (М1); угол загруженной площади (М2), точку внутри контура загружения на расстоянии 0,25b и 0,25l от центра (М3); точку М4 за контуром прямоугольника нагрузки на расстоянии 0,25l и 0,25b от угла. Построения эпюр выполнить до глубины ≤10м.
) по осям, проходящим через: центр загруженной площади (М1); угол загруженной площади (М2), точку внутри контура загружения на расстоянии 0,25b и 0,25l от центра (М3); точку М4 за контуром прямоугольника нагрузки на расстоянии 0,25l и 0,25b от угла. Построения эпюр выполнить до глубины ≤10м.
Решение для оси через М1:

| Относительная длина  .
Толща грунта разбивается на условные слои .
Толща грунта разбивается на условные слои 
 принимаются по таблице 10.2.
Расчеты приведены в табличной форме: принимаются по таблице 10.2.
Расчеты приведены в табличной форме:
|
Решение для оси через М2:

| Относительная длина  .
Толща грунта разбивается на условные слои .
Толща грунта разбивается на условные слои 
 принимаются по таблице 10.2.
Расчеты приведены в табличной форме: принимаются по таблице 10.2.
Расчеты приведены в табличной форме:
|
Решение для оси М3:

| Точка М3 является угловой для 4-х прямоугольников загрузки
 Мощность условного слоя
Мощность условного слоя 
 Расчеты приведены в табличной форме: Расчеты приведены в табличной форме:
| |||||||||

| 
| 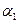
| 
| 
| 
| 
| 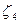
| 
| 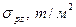
| |
| 1,0 2,0 3,0 4,0 5,0 6,0 7,0 | 1,6 3,2 4,8 6,4 8,0 9,6 11,2 | 1,00 0,588 0,232 0,118 0,070 0,046 0,032 0,024 | 1,0 2,0 3,0 4,0 5,0 6,0 7,0 | 1,00 0,795 0,469 0,284 0,181 0,125 0,090 0,068 | 0,533 1,067 1,600 2,133 2,667 3,200 3,733 | 1,00 0,899 0,756 0,558 0,412 0,308 0,232 0,182 | 1,6 3,2 4,8 6,4 8,0 9,6 11,2 | 1,00 0,638 0,358 0,227 0,155 0,109 0,082 0,062 | 40,0 29,20 18,95 11,87 8,19 5,88 4,36 3,36 | |
Решение для оси М4:
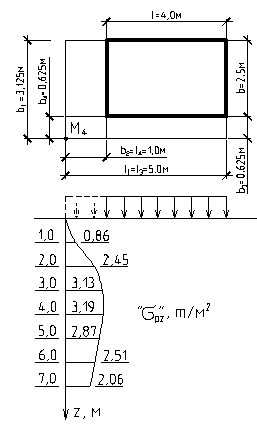
| Влияние на напряжение по оси М4 оказывают 4-е прямоугольника:
 Мощность условного слоя
Мощность условного слоя  Расчеты приведены в табличной форме:
Расчеты приведены в табличной форме:
| |||||||||

| 
| 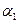
| 
| - 
| 
| - 
| 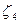
| 
| 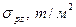
| |
| 1,0 2,0 3,0 4,0 5,0 6,0 7,0 | 0,32 0,64 0,96 1,28 1,60 1,92 2,24 | 1,00 0,983 0,912 0,797 0,673 0,558 0,463 0,385 | 1,0 2,0 3,0 4,0 5,0 6,0 7,0 | 1,00 0,814 0,528 0,352 0,241 0,178 0,134 0,103 | 1,6 3,2 4,8 6,4 8,0 9,6 11,2 | 1,00 0,641 0,371 0,250 0,184 0,139 0,110 0,100 | 1,6 3,2 4,8 6,4 8,0 9,6 11,2 | 1,00 0,558 0,232 0,118 0,071 0,046 0,032 0,024 | 0,86 2,45 3,13 3,19 2,87 2,51 2,06 | |
Пример 3.
Поверхность грунта загружена равномерно распределенной нагрузкой  по площади прямоугольника с размерами сторон
по площади прямоугольника с размерами сторон 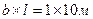 . Определить сжимающие напряжения по осям, проходящим через: центр площади загружения (М1); на контуре площади нагружения по средине длины (М2), под углом площади загружения (М3); за контуром прямоугольника нагрузки по средине длины на расстоянии 1м от центра (М4).
. Определить сжимающие напряжения по осям, проходящим через: центр площади загружения (М1); на контуре площади нагружения по средине длины (М2), под углом площади загружения (М3); за контуром прямоугольника нагрузки по средине длины на расстоянии 1м от центра (М4).
Решение для оси через М1:

| Точка М1 расположена в центре площади нагружения
Коэффициент
|
Решение для оси через М2:

| Точка М2 удалена от краев прямоугольника нагружения на
|
Решение для оси через М3:

| Точка М3 угловая. Расчет напряжений по оси М3 выполняется как для угловых точек прямоугольной нагрузки
|
Решение для оси через М4:

| Точка М4 расположнена на оси y на удалении 1,0м от центра подошвы. Напряжение определяется по схеме влияния полосовой нагрузки
Изменение глубины точек по оси М4 принимается с шагом
|
Пример 4.
Основание состоит из 3-х слоев грунта с поверхности залегает слой песка мелкого:  мощность слоя 3,0м. Ниже залетает слой суглинок:
мощность слоя 3,0м. Ниже залетает слой суглинок:  мощность слоя 4,8м. Под слоем суглинка залегает слой супеси
мощность слоя 4,8м. Под слоем суглинка залегает слой супеси  . Уровень грунтовых вод на глубине 1,5м от поверхности. Построить эпюру напряжений сжатия на горизонтальных площадках (
. Уровень грунтовых вод на глубине 1,5м от поверхности. Построить эпюру напряжений сжатия на горизонтальных площадках ( ).
).
Решение:

| - Песок под водой испытывает взвешивающее действие 
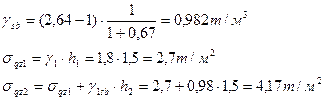 - Суглинок под водой не испытывает взвешивающего действия воды
- Суглинок под водой не испытывает взвешивающего действия воды 
 - Супесь под водой испытывает взвешивающее действие воды
- Супесь под водой испытывает взвешивающее действие воды

|
Пример 5.
Основание состоит из суглинка  , подстилаемого супесью
, подстилаемого супесью  , подстилаемой слоем песка мелкого
, подстилаемой слоем песка мелкого  . Характеристики грунтов принять из примера 4. Уровень грунтовых вод на глубине 1,5м от поверхности. Построить эпюру сжимающих напряжений
. Характеристики грунтов принять из примера 4. Уровень грунтовых вод на глубине 1,5м от поверхности. Построить эпюру сжимающих напряжений  от собственного веса грунта.
от собственного веса грунта.
Решение:
Суглинок не подвержен взвешивающему действию 
|
|
|

Супесь испытывает взвешивающее действие воды 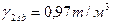

Песок мелкий испытывает взвешивающее действие воды 


|
|
|
|







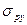

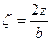
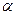



 -распределение напряжений принимается для случая нагружения по полосе
-распределение напряжений принимается для случая нагружения по полосе
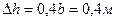


 - расчет напряжений выполняется для случая полосовой нагрузки
- расчет напряжений выполняется для случая полосовой нагрузки  - принимается по таблице 10.2. Изменение глубины по оси принимается с шагом
- принимается по таблице 10.2. Изменение глубины по оси принимается с шагом 






