Главная | Обратная связь | Поможем написать вашу работу!

Определение допускаемых напряжений

2.1. Выбор твердости, термообработки и материала колес.

Сталь в настоящее время – основной материал для изготовления зубчатых колес. В мало- и средненагруженных передачах, а также в открытых передачах с большими колесами применяют зубчатые колеса с твердостью материала Н ≤350 НВ. При этом обеспечивается чистовое нарезание зубьев после термообработки, высокая точность изготовления и хорошая обрабатываемость зубьев.

Для равномерного изнашивания зубьев и лучшей их прирабатываемости твердость шестерни НВ₁ назначается больше твердости колеса НВ₂. Разность средних твердостей рабочих поверхностей зубьев шестерни и колеса при твердости материала Н ≤350 НВ в передачах с прямыми и непрямыми зубьями составляет НВ_1ср - НВ_2ср=20…50. Соотношение твердостей в единицах НВ и HRC_э приведено на рисунке 2.1.

Рис. 2.1. – График соотношения твердостей в единицах НВ и HRC_э

Материал и его характеристики для изготовления зубчатых колес выбираются в зависимости от расположения зубьев на ободе колеса пары (прямые или непрямые) и номинальной мощности электродвигателя в следующем порядке:

а) выбрать материал для зубчатой пары колес, одинаковый для шестерни и колеса (табл. 2.1), но с разными твердостями, т.к. твердость зубьев шестерни должна быть больше твердости зубьев колеса (табл. 2.2);

Таблица 2.1

Выбор материала, термообработки и твердости

Параметр	Для передач с прямыми и непрямыми зубьями при малой (Р≤2 кВт) и средней (Р≤7,5 кВт) мощности	Для передач с непрямыми зубьями при средней (Р≤7,5 кВт) мощности
Шестерня	Колесо	Шестерня	Колесо
Материал	Стали 35, 45, 35Л, 40Л, 40, 40Х, 40ХН, 35ХМ, 45Л	Стали 40Х, 40ХН, 35ХМ
Термообработка	Нормализация, улучшение	Улучшение+ +закалка ТВЧ	Улучшение
Твердость	Н ≤350 НВ НВ_1ср - НВ_2ср=20…50	Н ≥45 HRC_э, Н ≤350 НВ НВ_1ср - НВ_2ср≥70
Допускаемое напряжение при числе циклов перемены напряжений N _Н0, N _F₀, Н/мм²	[ σ ]_Н0	1,8 НВ_ср+67	14 HRC_э+170	1,8 НВ_ср+67
[ σ ]_F₀	1,03 НВ_ср	при т ≥3 мм	1,03 НВ_ср
при т <3 мм

Таблица 2.2

Рекомендуемые сочетания материалов

Материал шестерни	Материал колеса
40Х 40ХН	35, 40Л, 45Л, Ст5 40, 45, 45Л, Ст6 55, 40ХЛ 40Х, 45Х

б) выбрать термообработку для зубьев шестерни и колеса по табл. 2.1 и табл. 2.2;

в) выбрать интервал твердости зубьев шестерни НВ₁ и колеса НВ₂ по табл. 2.3;

г) определить среднюю твердость зубьев шестерни НВ_1ср и колеса НВ_2ср по формуле, при этом надо соблюсти необходимую разность средних твердостей зубьев шестерни и колеса:

, (2.1)

где НВ_min и НВ_max – минимальное и максимальное значение диапазона твердости выбранного материала;

д) из табл. 2.3 определить механические характеристики сталей для шестерни и колеса.

2.2. Определение допускаемых контактных напряжений.

Допускаемые контактные напряжения при расчетах на прочность определяются отдельно для зубьев шестерни [ σ ]_Н1 и колеса [ σ ]_Н2.

Определить срок службы привода (ресурс), ч:

, (2.2)

где t _с – средняя продолжительность работы, ч.

Из полученного значения L _h следует вычесть 10…25 % часов на профилактику, текущий ремонт, нерабочие дни.

Определить коэффициент долговечности для зубьев шестерни и колеса:

, (2.3)

где N _H₀ – число циклов перемены напряжений, соответствующий пределу выносливости (табл. 2.4); N – число циклов перемены напряжений за весь срок службы (наработка),

. (2.4)

Таблица 2.3

Механические характеристики некоторых марок сталей для изготовления зубчатых колес и других деталей

Марка стали	Вид заготовки	Заготовка шестерни	Заготовка колеса	Термообработка	Твердость заготовки (зубьев)	σ _H	σ_F	σ _-1
поверхности	сердцевины	МПа
	Поковка	Любые размеры	Нормализация	163…192 НВ
			Улучшение	192…228 НВ
	Любые размеры	Нормализация	179…207 НВ
			Улучшение	235…262 НВ
			Улучшение	269…302 НВ
40Х			Улучшение	235…262 НВ
40Х			Улучшение	269…302 НВ
40Х			Улучшение + + Закалка токами высокой частоты	45…50 HRC_э	269…302 НВ
40ХН			Улучшение	235…262 НВ
40ХН			Улучшение	269…302 НВ
40ХН			Улучшение + + Закалка токами высокой частоты	48…53 HRC_э	269…302 НВ
35ХМ			Улучшение	235…262 НВ
35ХМ			Улучшение	269…302 НВ
35ХМ			Улучшение + + Закалка токами высокой частоты	48…53 HRC_э	269…302 НВ
35Л	Литье	Любые размеры	Нормализация	163…207 НВ
40Л	Любые размеры	Нормализация	147 НВ
45Л			Улучшение	207…235 НВ
40ГЛ			Улучшение	235…262 НВ

Таблица 2.4

Значение числа циклов N _H₀

Средняя твердость поверхности зубьев	НВ_ср
HRC_э	-
N _H₀, млн. циклов		16,5	36,4

Для нормализованных или улучшенных колес , для колес с поверхностной закалкой .

Если N > N _H₀, то принять .

По табл. 2.1 определить допускаемое контактное напряжение [ σ ]_Н0, соответствующее пределу контактной выносливости при числе циклов перемены напряжений N _H₀.

. (2.5)

Определяем допускаемые контактные напряжения [ σ _Н] для зубьев шестерни и колеса:

. (2.6)

Цилиндрические и конические зубчатые передачи с прямыми и непрямыми зубьями при НВ_1ср - НВ_2ср=20…50 рассчитывают по наименьшему значению [ σ _Н] из полученных для шестерни [ σ _Н1] и колеса [ σ _Н2], т.е. по менее прочным зубьям.

Зубчатые передачи с непрямыми зубьями при разности средних твердостей рабочих поверхностям зубьев шестерни и колеса НВ_1ср - НВ_2ср≥70 и твердости зубьев колеса Н ≤350 НВ рассчитывают по среднему допускаемому контактному напряжению:

. (2.7)

При этом [ σ _Н] не должно превышать 1,23[ σ _Н2] для цилиндрических косозубых колес и 1,15[ σ _Н2] для конических колес с непрямыми зубьями.

2.3. Определение допускаемых напряжений изгиба.

Определим коэффициент долговечности для зубьев шестерни и колеса:

, (2.8)

где N _F₀ =4·10⁶ – число циклов перемены напряжений для всех сталей, соответствующее пределу выносливости.

При твердости Н ≤350 НВ принимают , при твердости Н>350 НВ . Если N > N _F₀, то принимают .

Определим допускаемое напряжение изгиба [ σ _F₀], соответствующее пределу изгибной выносливости при числе циклов перемены напряжений N _F₀ по табл. 2.1:

. (2.9)

Определяем допускаемые напряжения изгиба [ σ _F] для зубьев шестерни и колеса:

. (2.10)

Расчет модуля зацепления для цилиндрических и конических зубчатых передач с прямыми и непрямыми зубьями выполняют по наименьшему значению [ σ _F] из полученных для шестерни [ σ _F₁] и колеса [ σ _F₂], т.е. по менее прочным зубьям.

Расчет зубчатой передачи

3.1. Определение межосевого расстояния.

, (3.1)

где – вспомогательный коэффициент, К _а=43 – для косозубых передач, К _а=49,5 – для прямозубых передач; – коэффициент неравномерности нагрузки по длине зуба (табл. 3.1); – коэффициент ширины венца, М – вращающий момент на валу, Н·м.

Табл. 3.1

Ориентировочные значения коэффициента для зубчатых передач

редукторов, работающих при переменной нагрузке

Расположение зубчатых колес относительно опор	Твердость НВ поверхностей зубьев
≤350	>350
Симметричное	1,00…1,15	1,05…1,25
Несимметричное	1,10…1,25	1,15…1,35
Консольное	1,20…1,35	1,25…1,45

Коэффициент ширины венца рекомендуется выбирать из ряда по ГОСТ 2185-66: 0,10; 0,125; 0,16; 0,25; 0,315; 0,40; 0,50; 0,63; 0,80; 1,00; 1,25.

Для прямозубых передач рекомендуется ограничивать ≤0,25; для косозубых предпочтительно принимать =0,25…0,63.

Полученное значение округляют до ближайшего стандартного значения по ГОСТ 2185-66 (в мм) для одноступенчатых редукторов:

1-й ряд: 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500.

2-й ряд: 71, 90, 112, 140, 180, 224, 280, 355, 450, 560, 710, 900, 1120, 1400, 1800, 2240.

Первый ряд следует предпочитать второму.

Таблица 3.2

Рекомендуемые значения межосевых расстояний двухступенчатых

редукторов ГОСТ 2185-66

Вх. ст.				(140)	(180)
Вых. ст.				(225)	(280)
Вх. ст.	(225)	(280)	(355)	(450)	(560)
Вых. ст.	(355)	(450)	(560)	(710)	(900)

Таблица 3.3

Рекомендуемые значения межосевых расстояний трехступенчатых

редукторов ГОСТ 2185-66

Вх. ст.				(140)
Пр. ст				(225)
Вых. ст.				(355)
Вх. ст.	(180)	(225)	(280)	(355)
Пр. ст.	(280)	(355)	(450)	(560)
Вых. ст.	(450)	(560)	(710)	(900)

3.2. Определение модуля зацепления.

Определим модуль зацепления по формуле:

(3.2)

Округляем полученное значение модуля зацепления до стандартного по ГОСТ 9563-60 (в мм):

1-й ряд: 1; 1,25; 2; 2,5; 3; 4; 6; 8; 10; 12; 16; 20.

2-й ряд: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 7; 9; 11; 14; 18; 22.

Первый ряд следует предпочитать второму.

3.3. Определяем угол наклона зубьев косозубой передачи

Угол наклона зубьев для косозубой передачи выбирают равным β =8…16°, угол наклона зубьев для прямозубой передачи β =0°.

3.4. Определяем суммарное число зубьев шестерни и колеса

, (3.3)

Округляем полученный результат до целого значения, числа зубьев не могут быть дробными.

3.5. Определяем число зубьев шестерни и колеса

Для шестерни:

; (3.4)

для колеса:

, (3.5)

Округляем полученные результаты до целого значения, числа зубьев не могут быть дробными.

Проверяем расчет:

, (3.6)

Уточняем передаточное число:

; (3.7)

Разница между выбранным стандартным значением передаточного числа и полученным не должна быть больше 5 %.

3.6. Уточняем действительную величину угла наклона зубьев косозубой передачи:

, (3.8)

3.7. Определяем торцевой модуль зацепления:

; (3.9)

3.8. Определим ширину венца шестерни и колеса.

Для колеса:

; (3.10)

для шестерни:

. (3.11)

3.9. Определяем диаметры делительных окружностей шестерни и колеса с точностью до сотых долей мм:

; (3.12)

; (3.13)

При расчете прямозубой передачи вместо торцевого модуля зацепления m_t используют нормальный модуль зацепления m_n.

3.10. Определяем фактическое межосевое расстояние.

После расчета делительных окружностей шестерни и колеса делают проверочный расчет межосевого расстояния:

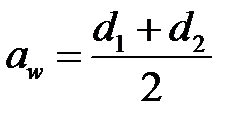. (3.14)

3.11. Расчет фактических основных геометрических параметров передачи для шестерни и зубчатого колеса.

Диаметр окружности вершин зубьев шестерни:

; (3.15)

для колеса:

. (3.16)

Диаметр окружности впадин зубьев шестерни:

; (3.17)

для колеса:

. (3.18)

3.12. Определим окружную скорость шестерни:

. (3.19)

колеса:

. (3.20)

3.13. Проверочный расчет.

Определим коэффициент, учитывающий динамическую нагрузку и неравномерность распределения нагрузки между зубьями по ширине венца:

. (3.21)

где – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; – динамический коэффициент.

Для прямозубых колес принимают =1,0; для косозубых колес в зависимости от окружной скорости ϑ: при ϑ = 10…20 м/с и 7-й степени точности =1,0…1,1, при ϑ < 10 м/с и 8-й степени точности =1,05…1,15.

Динамический коэффициент определяют в зависимости от окружной скорости колес ϑ и степени точности их изготовления.

Для прямозубых колес при ϑ < 5 м/с следует назначать 8-ю степень точности по ГОСТ 1643-81; при этом =1,05…1,10. При ϑ = 10…20 м/с и 7-й степени точности =1,05…1,1. Меньшие из указанных значений относятся к колесам с твердостью поверхностей зубьев НВ≤350, большие – при твердости НВ>350.