Построение правильного отсечения методом Гомори

 

Опишем способ построения правильного отсечения, предложенный Гомори. Для произвольного числа a, через [ a ] будем обозначать его целую часть, т.е. [ a ] есть наибольшее целое число k непревосходящее число a.

Дробной частью { a } числа a называется число { a } = a - [ a ]. Отметим очевидное свойство дробной части произвольного числа: 0£{ a }<1, причем { a } = 0 в том и только в том случае, когда a - целое число.

Пусть x^* - опорное решение задачи (1.1), (1.2), не являющееся целочисленным, 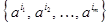 - его базис и B - соответствующая симплекс-таблица в координатной форме.

Рассмотрим приведенную систему уравнений, отвечающую данному базису (и таблице B) плана

 

x^*:

 

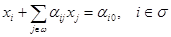
Поскольку x_j^* = 0 при j Îw, то нецелочисленными могут быть лишь величины x₀^* = < c, x^* >, x_i^*, i Îs.

Пусть s - такой индекс (0 £ s £ n), что число x_s^* - не целое. Рассмотрим s -ю строку в симплексной таблице B (s -е уравнение в системе (3.2), (3.3)) и составим выражение

Теорема 2. Если x Î X^* - целочисленный план задачи (1.1), (1.2), то

 

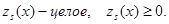
Доказательство. Используя соотношение

 

a _sj = [ a _sj ] + { a _sj }, j = 0, 1, 2, …, n, из (3.3) при i = s получаем

 

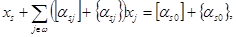
откуда

 

 

В левой части данного неравенства стоит целое число, следовательно, число

 

 

также целое. Из того, что x_j ³ 0, j Îw, используя свойство дробной части, получаем

 

 

т.е. - z_s (x) < 1, или z_s (x) > -1. Учитывая, что z_s (x) - целое, окончательно примем z_s (x) ³ 0.

Следствие. Если x_s^* (= a _s0) - нецелое число и Множество X^* планов целочисленной задачи (1.1)-(1.3) непусто, то среди чисел { a _sj }, j =1, 2, …, n, есть положительные.

В самом деле, все числа { a _sj }, очевидно неотрицательны. Допустим, что { a _sj } = 0, j = 1, 2, …, n.

Если X^* непусто и x^* Î X^*, то z_s (x^*)= - { a _s0 }, о том, что z_s (x^*) - целое число, так как 0 < { a _s0 } < 1.

Замечание. В доказательстве теоремы 2 мы воспользовали предположением II о том, что гарантирована целочисленность целевой функции. Действительно в случае s = 0 величина

 

 

является целой (при условии, что x Î X^*) лишь тогда когда число x₀ = < c, x > - целое.

Отсюда вытекает

Теорема 3. Если число x_s^* - нецелое, то неравенство

 

 

является правильным отсечением.

Доказательство. Проверим условие отсечения в определении 2. Так как x_s^* = a _s0, то из того, что x_s^* - нецелое, получаем неравенство { a _s0 } > 0. Поскольку x_j^* = 0 при j Î w, то

 

,

и поэтому вектор x^* не удовлетворяет неравенству (3.5). Условие правильности следует из утверждения z_s (x) ³ 0 в теореме 2.

 

Первый алгоритм Гомори

 

Перейдем к изложению первого алгоритма Гомори.

Обозначим задачу (1.1), (1.2) через L ₀. Гомори предложил на первом этапе своего алгоритма находить лексикографический максимум задачи L ₀. Будем обозначать через

x (0) = (x ₀(0), x ₁(0), …, x _n(0))

 

(n+1)-мерный вектор такой, что (x ₁(0), x ₂(0), …, x _n(0)) - решение лексикографической задачи L ₀, а x ₀(0) =  - значение линейной формы. В тех случаях когда это не вызывает недоразумения, будем называть x (0) - оптимальным планом лексикографической задачи L ₀ (хотя по общепринятой терминологии планом называется вектор, составленный из последних n координат вектора x (0)).

Отметим также, что x (0) будет являться опорным планом, а так же строго допустимым псевдопланом задачи L ₀.

Если x(0) - целочисленный вектор, то он, очевидно, и является решением задачи (1.1) - (1.3).

В противном случае отыскивается минимальный индекс s, 0 £ s £ n, для которого величина x_s (0) не является целой. Пусть B (0) - симплексная таблица в координатной форме, соответствующая вектору x (0). С помощью коэффициентов s -й строки этой таблицы (т.е. коэффициентов приведенной системы (3.2), (3.3)) приемом, описанным выше, строится правильное отсечение.

Вводится вспомогательная переменная x_{n +1} и рассматривается задача L ₁:

 

 

Следующий этап состоит в нахождении лексикографического максимума задачи L ₁. Важным достоинством алгоритма Гомори является тот факт, что начальный допустимый строгий псевдоплан для применения двойственного симплекс-метода к задаче L ₁ находится без труда. Действительно, легко видеть, что в качестве такого псевдоплана можно взять вектор

 

 

где

 

 

В самом деле, очевидно, что y (1) удовлетворяет (вместе с вектоорм x (0)) ограничениям (3.6), (3.7) задачи L ₁, а из ограничений (3.8) нарушается лишь одно: x_{n +1}(0)= - {a _{s 0}} < 0. Кроме того, y (1) является опорным для системы уравнений (3.6), (3.7), поскольку, если  - базис плана x (0) то система

 

линейно независима и служит базисом для y (1). Покажем, что y (1) - строго допустимый псевдоплан. С этой целью построим симплексную таблицу, соответствующую указанному базису вектора y (1). Для этого нужно лишь приписать снизу к таблице B (0) строку

 

 

Где w = { j ₁, j ₂, …, j_{n - m} } - список номеров небазисных переменных, соответствующих таблице B (0) опорного плана x (0). Поскольку x (0) - строго допустимый псевдоплан, то всякий столбец b ^j, j Îw, таблицы B (0) лексикографически положителен: b j > 0, j Îw. Отсюда вытекает, что и в симплексной таблице в координатной форме, отвечающей опорному вектору y (1), всякий столбец (кроме первого, совпадающего с y (1)) лексикографически положителен:

 

 

Таким образом, имея в своем распоряжении решение x (0) лексикографической задачи L ₀ и соответствующую симплекс таблицу в координатной форме B (0), без каких либо дополнительных вычислений находим начальный строго допустимый псевдоплан y (1) для задачи L ₁ и строим соответствующую ему симплексную таблицу в координатной форме.

Может случиться, что лексикографическая задача L ₁ не имеет решения. В этом случае решение целочисленной задачи (1.1) - (1.3) следует прекратить поскольку имеет место

Теорема 4. Если в задаче L ₁ не существует лексикографического максимума, то множество X ^* целочисленных точек задачи (1.1) - (1.3) пусто.

Доказательство. Поскольку множество X векторов, удовлетворяющих условиям Ax = b, x ³ 0, согласно предположению I ограничено, то ограниченным является и множество планов задачи L ₁. Поэтому единственной причиной, по которой эта задача может не иметь лексикографического минимума, может быть только то что множество ее планов пусто. Покажем что в таком случае множество X ^* также пусто.

Предположим противное, т.е. что X ^* ¹ Æ, и пусть x * = (x ₁^*, x ₂^*, …, x_n ^*) Î X*. По теореме 2 получаем, что величина

 

 

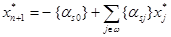
неотрицательна. Но это означает, что вектор = (x ₁^*, x ₂^*, …, x_n ^*, x_{n +1}^*) является планом задачи L ₁, в противоречие с вышесказанным. Теорема доказана.

Пусть x (1) = (x ₀(1), x ₁(1), …, x_n (1), x_{n +1}(1)) - решение лексикографической задачи L ₁. Отправляясь от задачи L ₁ и вектора x (1), аналогичным образом строятся задачи L_r, r = 2, 3, …, и решения x (r) Î Â ^{n +1+ r} соответствующим им лексикографическим задач.

Заметим, что алгоритм Гомори однозначно определяет последовательность x (r), r = 0, 1, 2, …, что следует из однозначности выбора s. Обратим так же внимание на то, что индекс s всегда не превосходит n: 0 s n. В самом деле, если все x_j (r) при j = 0, 1, 2, …, n - целые числа, то из теоремы 2 вытекает, что x_{n +1}(r), x_{n +2}(r), … - также целые.

Если на каком - то шаге r вектор

x (r) = (x ₀(r), x ₁(r), …, x_n (r), …, x_{n + r} (r))

 

оказывается целочисленным, то вектор (x ₀(r), x ₁(r), …, x_n (r)) является решением задачи (1.1) - (1.3). Доказательство этого утверждения очевидно.

Переход от вектора x (r) к вектору x (r +1) с помощью описанного алгоритма Гомори называется большой итерацией, в отличие от промежуточных итераций двойственного симплекс-метода, которые называются малыми.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: