 |
Доказательство конечности алгоритма
|
|
|
|
Основной вопрос, относящийся к первому алгоритму Гомори таков: всегда ли за конечное число больших итераций можно получить целочисленный вектор x (r).
Докажем конечность первого Алгоритма Гомори. Будем использовать следующие обозначения:
x (0) = (x 0(0), x 1(0), …, xn (0));
где (x 1(0), …, xn (0)) - решение лексикографической задачи L0, а x (0) =  - соответствующее значение линейной формы (целевой функции).
- соответствующее значение линейной формы (целевой функции).
y (1) = (x 0(0), x 1(0), …, xn (0), xn +1),
где

вектор y(1) служит начальным строго довпустимым псевдопланом при решении задачи L1 двойственным симплексным методом в координатной форме: ` y (1) = (` y 0(1), ` y 1(1), …, ` yn (1), ` yn +1(1)) - вектор, получающийся из y (1) в результате первой (малой) итерации двойственного симплекс метода в координатной форме.
Аналогично вводятся обозначения
x (r), y (r + 1), ` y (r + 1), r = 1, 2, …
Из свойств двойственного симплекс метода в координатной форме следует
y (r) >` y (r) ³ x (r).
Лемма 1. Пусть s - минимальный индекс, для которого число xs(0) - не целое. Тогда
 .
.
Доказательство. Поскольку из (3.9) следует y (1) >` y (1), то возможно два случая:
 1..
1..
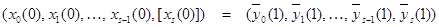 2..
2..
В случае 1 утверждение леммы выполняется тривиально по определению лексикографического порядка.
Рассмотри случай 2. Согласно правилам двойственного симплекс-метода на первой (малой) итерации решения задачи L 1 выводу из числа базисных подлежит переменная xn +1, поскольку в векторе y (1) xj (0) ³ 0, j Î w, xn +1 < 0. Пусть k Î w - такой индекс, что


Для любого j Î w, если -{a sj } < 0. По правилам симплексного метода в число базисных вводится переменная xk.
Случай 2 возможен лишь при условии b ik = 0, i = 0, 1, 2, …, s - 1. Поскольку x (0) - строго допустимый псевдоплан задачи L 0, то все ее столбцы b j, j Î w, симплекс таблицы B (0) лексикографически положительны; в частности b k > 0. Следовательно, координата b sk данного столбца должна быть неотрицательной. Заметим, что b sk = a sk (т.е. 0 £ s £ n и s Î w), по условию (3.10) число a sk - не нуль. Поэтому
|
|
|
a sk > 0 и a sk ³ {a sk }
По формуле преобразования симплекс-таблицы имеем
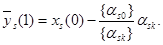
Вспоминая, что xs(0) = as0, получаем:
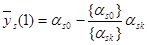 .
.
С учетом (3.11) получим оценку:
 .
.
Лемма доказана.
Замечание. Если исходная задача (1.1) - (1.3) допустима, то согласно следствию из теоремы 2 индекс k, удовлетворяющий условию (3.10), существует.
Следствие. Справедливо соотношение

Действительно при r = 1 это неравенство вытекает из леммы и второго неравенства (3.9). Что бы получить это утверждение при произвольном r, нужно воспользоваться тем, что yj (r) = xj (r) при 0 £ j £ n, и неравенством y (r) ³ x (r) в (3.9).
Теорема 5. Если выполнены предположения I и II, то первый алгоритм Гомори требует лишь конечного числа больших итераций.
Что бы убедиться в истинности теоремы, необходимо показать, что при некотором r вектор x (r) = (x 0(r), x 1(r), …, xn + r (r)) - целочисленный. Для этого, в свою очередь, достаточно доказать целочисленность вектора (x 0(r), x 1(r), …, xn (r)), поскольку из теоремы 2 тогда вытекает, что все числа xn +1(r), xn +2(r), …, xn + r (r) также целые. Вспомним также, что минимальный индекс s, при котором число xs(r) - нецелое, всегда не превосходит n: 0 £ s £ n. Прежде чем переходить к основному доказательству докажем следующую лемму:
Лемма 2. Для любого j, 0 £ j £ n, существует такой номер Rj, что при r ³ Rj все числа xj (r) - целые и равны одному и тому же целому числу xj (Rj).
Доказательство. Пусть s, 0 £ s £ n, - минимальный индекс для которого утверждение Леммы не выполняется. Обозначим

В том случае когда s = 0, положим R = 0.
Пусть r, l - такие индексы, что R £ r £ l, и числа xs (r), xs (l) - нецелые. Покажем, что тогда [ xs (r)] > [ xs (l)]. Действительно по определению s имеем
|
|
|
 .
.
В таком случае s - минимальный индекс, для которого число xs (r) - нецелое. По следствию из леммы 1 имеем [ xs (r)] ³ xs (l).
Учитывая, что xs (l) - не целое число, имеем xs (l) > [ xs (l)], откуда и получаем нужное утверждение. Поскольку множество X планов задачи (1.1) - (1.3) ограничено, то ограничена любая величина xs (r), 0 £ s £ n, r = 1, 2, …. Поэтому бесконечной цепочки неравенств вида [ xs (r)] > [ xs (l)] > … существовать не может, а, следовательно, в последовательности xs (r), r = 0, 1, …, не может быть бесконечно много нецелых чисел. Аналогично доказывается, что в этой последовательности не может быть бесконечно много различных целых чисел.
Лемма доказана.
Вернемся к доказательству теоремы. Пусть
 ,
,
где числа Rj фигурируют в формулировке леммы 2. Тогда согласно этой лемме все числа xj (R), 0 £ j £ n, - целые. Из теоремы 2 получаем, что вектор x (R) - целочисленный. Следовательно алгоритм Гомори требует не более R итераций.
Теорема доказана.
|
|
|


