 |
Замечания по практической реализации первого алгоритма Гомори
|
|
|
|
При практической реализации первого алгоритма Гомори важной проблемой является нарастание количества ограничений, что ведет к увеличению размеров симплексных таблиц. Гомори предложил способ устранения этого недостатка алгоритма, заключающийся в следующем.
) В ходе решения задачи Lr двойственным симплексным методом на каждой малой итерации следует пользоваться уточненным правилом вывода из числа базисных векторов для решения задач линейного программирования симплекс-методом: если в первом столбце симплексной таблицы имеется несколько отрицательных элементов b i 0 (= xi), i =1, 2, …, n, …, n + r, то выводить из числа базисных надо переменную с минимальным номером.
) Если в ходе очередной малой итерации при реализации задачи Lr все основные переменные x 1, x 2, …, xn оказались неотрицательными, то дальнейшее применение двойственного симплекс-метода к задаче Lr следует прекратить, несмотря на то, что ее лексикографический максимум, быть может, еще не достигнут. Если при этом все переменные xj, j = 1, 2, …, n, оказались целочисленными, то по теореме 2 все вспомогательные переменные xn + k , k = 1, 2, …, r, целочисленны и неотрицательны. Это означает, как уже известно, что вектор (x 0, x 1, x 2, …, xn) является решением исходной целочисленной задачи. В противном случае переходим к новой большой итерации.
) Строка симплексной таблицы, соответствующая вспомогательной переменной xn + r , удаляется, как только переменная xn + r объявляется небазисной. Напомним, что это происходит на первой же малой итерации решения задачи Lr.
) Если в ходе решения задачи Lr переменная xn + r вновь попадает в число базисных, то то соответствующая ей строка не восстанавливается.
|
|
|
Понятно, что при выполнении правил 3), 4) размеры симплексной таблицы в первом алгоритме Гомори не увеличиваются - в каждой таблице содержится n + 2 строк, отвечающие основным переменным x 0, x 1, …, xn и текущей вспомогательной переменной xn + r в момент ее введения) и n - m +1 столбцов (поскольку число n - m небазисных переменных не меняется).
) На первой малой итерации решения задачи Lr +1 в качестве переменной, выводимой из базиса, выбирается именно xn + r +1, не смотря на то, что значения остальных вспомогательных переменных в этот момент так же могут быть отрицательными.
Заметим, что правило 5) на самом деле избыточно, поскольку при выполнении правил 3) и 4) мы ничего не знаем о значении остальных переменных xn +1, …, xn + r в момент перехода к задаче Lr +1. Данное правило выделено лишь для того, чтобы подчеркнуть отличие рассматриваемых алгоритмов.
Отметим, что при использовании правила 2) возникающая последовательность x ’(r) может не быть лексикографическим максимумом задачи Lr, поскольку значения некоторых из вспомогательных переменных могут быть отрицательными.
Тем не менее, для последовательности x ’(r), r = 0, 1, 2, …, получаемой с использованием правил 1) и 2), сохраняется важное свойство: эта последовательность единственна.
Осталось лишь доказать, что при использовании правил 1) - 4) алгоритм Гомори остается конечным, поскольку его конечность и будет означать, что он приводит к цели - нахождению целочисленного решения задачи (1.1) - (1.3). В самом деле, конечность числа R больших итераций означает, что вектор x ’(R) целочисленный.
Отметим, во-первых, что при использовании правила 2) число малых итераций решения задачи Lr конечно - не больше, чем требуется для нахождения ее лексикографического максимума.
Теорема 6. Последовательность x’(r), возникающая в процессе применения алгоритма Гомори, уточненного правила 1) - 4), конечна.
Доказательство. Заметим, что в доказательстве теоремы 5 о конечности последовательности x(r) использовались лишь два обстоятельства, регулирующие возникновение этой последовательности: способ построения правильного отсечения и тот факт, что во всякой текущей симплекс-таблице вс столбцы b j, j Îw, лексикографически положительны. Таким образом, удаление строки, соответствующей вспомогательной переменной, может повлиять лишь на последнее обстоятельство. Этого, однако, так же быть не может, как показано в следующей лемме.
|
|
|
Лемма 3. В любой симплекс-таблице, возникающей в ходе алгоритма Гомори, уточненного правилами 1) - 4), для любого столбца

имеет место неравенство
 .
.
Доказательство. Допустим, что утверждение леммы не выполняется для некоторого k Î w. Поскольку b k, то данное предположение означает, что

По определению симплексной таблицы в координатной форме, имеем
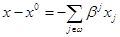
Для любого x Î Rn +1+ r , если утверждение леммы нарушается в ходе решения задачи Lr. Формула (3.13) с учетом (3.12) означает, что изменение значения переменной xk не влияет на значение xi, i = 0, 1, 2, …, n. Другими словами, при одном и том же наборе величин xi, 0£ i £ n, переменная xk может принимать произвольное значение. Отсюда следует, во-первых, что k ³ n + 1, а во-вторых, что принятое допущение (3.13) неверно, поскольку поскольку значение любой вспомогательной переменной xk, k ³ n + 1, как вытекает из (3.7), однозначно определяется значениями основных переменных.
Поскольку удаление строк, соответствующих вспомогательных переменным, не влияет на свойство столбцов b j, j Î w, быть лексикографически положительными, то эти строки вообще не нужны. Действительно, с учетом правил 1) - 2) переменная xn + r , попав в число базисных, так и остается базисной до конца вычислений, и ее строка не потребуется для определения переменной, вводимой в базис согласно правилам симплекс-метода.
Таким образом, элементы строки, соответствующие переменной xn + r , не участвуют в формулах двойственного симплекс-метода для вычисления значений всех остальных переменных.
Поскольку, как отмечалось, индекс s, регулирующий формирование правильного отсечения, не превосходит n, 0 £ s £ n, то и для этих целей вспомогательные переменные не потребуются.
|
|
|
Реализация на ЭВМ
В данном курсовом проекте программа предназначена для нахождения решения целочисленной задачи линейного программирования методом Гомори.
В программном модуле используется алгоритм описанный в теоретической части с учетом замечаний по практическому применению метода, сделанных Гомори.
Ввод данных в программном модуле производится из файла. Вывод результатов работы программы может производится в файл, на дисплей или на принтер. Формат входного файла:
<m> <n>
<c1> <c2> … <cn>
<a11> <a21> … <an1> <b1>
<a12> <a22> … <an2> <b2>
…
<a1m> <a2m> … <anm> <bm>
где n - количество переменных, m - количество ограничений, c 1, c 2, …, cn - коэффициенты максимизируемой линейной формы, aij - элементы матрицы A, bj - компоненты вектора b. A, b - характеризуют ограничения [см. (1.2)].
Пример входного файла:
9
2 5 0 0 0 0 0 0 0
3 1 0 0 0 0 0 0 12
2 5 0 1 0 0 0 0 0 30
3 2 0 0 1 0 0 0 0 22
2 -1 0 0 0 1 0 0 0 12
1 -3 0 0 0 0 1 0 0 0
2 5 0 0 0 0 0 -1 0 10
5 1 0 0 0 0 0 0 -1 5
Список литературы:
1. Абрамов Л.А., Капустин В.Ф. Математическое программирование. - Л.: Изд-во ЛГУ, 1981. -328 с.
. Белоусова Г.С. Линейное программирование. Учебное пособие. -Красноярск: Наука, 1975. -107 с.
. Кузнецов Ю.Н. и др. Математическое программирование: Учебное пособие. - 2-е изд., перераб. и доп. -М.: Высшая школа, 1980. -300 с.
. Ашманов С.А., Линейное программирование. М.: Наука. 1969. -240 с
. Габасов Р.И. Кириллова Ф.М., Методы линейного программирования. Минск: Наука. 1977. -174 с
|
|
|


